Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2777.
Christiaan Huygens au marquis de l'Hospital.
29 décembre 1692.

La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre est la réponse au No. 2775.
De l'Hospital y répondit le 12 février 1693.

A la Haye, le 29 Dec. 1692.

Je reconnois de plus en plus Monsieur le grand progrez que vous avez fait dans ces belles subtilitez de la geometrie qui la portent si loin au delà de ce qu'elle a estè cy-devant. La derniere solution de vostre Probleme est encore meilleur que la premiere et je vous suis obligè d'avoir bien voulu m'indiquer le moien dont vous vous estes servi pour y parvenir. Je vois qu'il sert en plusieurs autres cas; mais l'aiant essaiè à trouver la somme des √aa+yy dy/y, qui seroient les pe-

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 244.

[p. 349]

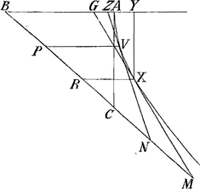
tites tangentes de la portion de la Logarithmique, sans les diviser en deux, comme vous avez fait²⁾, je suis venu à la quadrature d'une courbe fort composée, qu'on ne voit pas qu'elle depende de la quadrature de l'hyperbole³⁾. Mais j'ay remarquè en mesme temps que la dite somme des √aa+yy dy/y ne depend que de la quadrature d'une courbe dont l'equation est a⁴+aayy ∞ xxyy⁴⁾, que j'ay trouvè il y a longtemps qu'elle depend de celle de l'hyperbole⁵⁾. Ainsi sans tout ce subtil detour que vous avez suivi Monsieur, l'on peut resoudre vostre probleme⁶⁾. Mais ce que j'ay admirè, l'on vient à vostre mesme derniere construction, qui s'abrege encore un peu en prenant EC pour BI dans vostre figure⁷⁾ DG pour AK⁸⁾.

2) Voir la Lettre N^o. 2765, au commencement de la ‘demonstration’.

3) On rencontre cet essai infructueux à la page 153 du livre H, où la somme des √a²+y² dy:y est réduite, par la substitution yz:a+a=√a²+y², à la quadrature de la courbe: x=a²(a²+z²)²:z(a²-z²)²; après quoi Huygens ajoute: ‘Ergo sic ad curvam valde compositam et ignotae quadraturae reductum fuisset problema dimensionis lineae Logarithmicae si, ut hic, non fuisset divisa λ[=dy]√aa+yy:y in duas.

4) En effet, pour réduire la somme mentionnée à la quadrature ∫xdy de cette courbe, il suffit de poser x=a√a²+y²:y, d'où il suit a⁴+a²y²=x²y².

5) Voir l'Appendice I à cette lettre, notre pièce N^o. 2778, qui date, d'après le lieu qu'il occupe dans le livre H, de septembre ou d'octobre 1692. Aucune trace d'un traitement antérieur du même problème n'a été rencontrée dans les manuscrits.

6) Voir la pièce N^o. 2779, Appendice II à cette lettre, où nous avons reproduit la solution définitive de Huygens du problème en question.

7) Probablement Huygens veut dire ici qu'on peut simplisier la construction de de l'Hospital en agissant de sorte que EC, dans la figure de la Lettre N^o. 2775, s'identifie avec la plus courte des deux lignes (AK et BI) dont la différence, ajoutée à TG-TE, va fournir la longueur de l'arc CD. Et il est clair que cette remarque devait amener, presque nécessairement, la construction abrégée qu'on rencontre quelques lignes plus loin dans le texte de la présente lettre. En effet, pour que la différence AK-CE de la figure de Huygens (celle de la page suivante de la présente lettre) devienne égale à la différence AK-BI de la figure de de l'Hospital (celle de la Lettre N^o. 2775), il suffit qu'on ait EL:KL (figure de Huygens)=LI:KL (figure de de l'Hospital). Posons donc dans la figure de de l'Hospital: LG=y₁ (=LD figure de Huygens), LE=y₂ (=LE figure de Huygens), GH=LI=z₁, EF=LK=z₂, où (d'après la note 3 de la Lettre N^o. 2775), yz/a+a=√a²+y², alors il faut qu'on ait, dans la figure de Huygens, EL:KL=z₁:z₂; donc KL=EL×z₂/z₁=y₂z₂/z₁=√a²+y₂²-a/√a²+y₁²-a×y₁=TE-TL/TD-TL× × DL (toujours dans la figure de Huygens, où manque la lettre T, voir la note 10)=TO-TL/TP-TL×DL (en prenant TO=TE, TP=TD)=OL/PL×DL, d'où la construction abrégée mentionnée suit immédiatement.

8) Cette addition est due probablement à quelque inadvertance.

[p. 350]

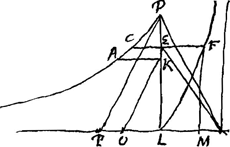Ce que vous dites de la quadrature de l'espace FLM, dans vostre mesme figure, je le trouve veritable, et que la construction se peut un peu abreger, à peu près de mesme que celle dont je viens de parler. Mon calcul en cecy m'a menè par la courbe 2a³ ∞ aax-zzx et par l'hyperbole⁹⁾. Puis que j'ay tracè la figure¹⁰⁾, je puis en 3 mots adjouter a quoy se reduit vostre construction de l'autre probleme. C'est qu'aiant pris TP ∞ TD et TO ∞ TE, je mene OK parallele à PD et j'applique les lignes EC, KA, alors la difference des KA, EC, avec PO font ensemble la longueur de la courbe DC¹¹⁾. Mais ces constructions sont peu de chose apres la solution du probleme.

Vous auez fort bien et savemment resolu toutes les questions que je vous avois proposées, et il paroit que vous avez aussi la regle de Mr. Fatio¹²⁾ que Mr. Leibnits n'a pas¹³⁾. Vous ne pouvez non plus ignorer, Mons.^r, comme je crois, une methode peu connuë¹⁴⁾, que j'ay debrouillée il n'y a pas long-

9) Voir l'Appendice III à cette lettre (notre pièce N^o. 2780), datée du 18 décembre 1692.

10) Il y manque la Lettre T au bout droit de la droite POLM.

11) L'origine probable de cette construction à déjà été indiquée dans la note 7. Ajoutons que la courbe LF, quoique tracée dans la figure, ne joue plus aucun rôle dans la construction.

12) On peut consulter sur cette règle les Lettres N^o. 2465, note 11; N^o. 2660, note 17 et N^o. 2677, note 9.

13) Comparez la Lettre N^o. 2733.

14) D'après les annotations que l'on rencontre dans le livre H, et que nous avons reproduites dans les §§ VII, VIII et IX de la pièce N^o. 2781, il s'agit ici d'une méthode, exposée par Fermat dans le traité mentionné dans la note 27 de la Lettre N^o. 2693, aux pages 51-57 des Opera Varia (p. 271-285, Tome I de l'édition récente des OEuvres de Fermat par Tannery et Henry).
Cette méthode est fondée sur un théorème qui équivaut, en notation moderne, à la relation:

y^m dx=x₂y₂^m-x₁y₁^m-mxy^m-1 dy,

où les intégrations sont supposées s'étendre le long d'une courbe quelconque.
Voici un exemple de l'emploi que Fermat propose de faire de ce théorème pour déduire des quadratures nouvelles: Il part de l'équation y³=a⁵x^-2-a⁶x^-3, pour laquelle l'intégrale ∫y³dx se calcule facilement au moyen de la quadrature connue des courbes x^py^q=a^p+q, dont la théorie est exposée plus haut dans le même traité déjà mentionné. On connaît donc de même, à l'aide du théorème, l'intégrale ∫xy²dy, c'est-à-dire, en posant u=a^-2xy², la quadrature ∫udy d'une courbe dont l'abscisse est égale à u.
Or, si l'on cherche l'équation de cette dernière courbe, en substituant x=a²uy^-2 dans celle de la courbe donnée, on arrive à l'équation y³+u³-auy=0, qui représente le folium de Descartes. Seulement Fermat n'exécute pas les calculs nécessaires pour achever la quadrature du folium et se borne dans cet exemple, comme dans les autres, à des indications générales.

[p. 351]

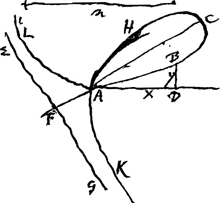
temps¹⁵⁾; qui sert grandement dans ces recherches des quadratures¹⁶⁾, des centres de gravitè¹⁷⁾ et du probleme renversè des Tangentes. C'est de la que j'ay pris cette derniere quadrature que je viens de raporter¹⁸⁾, et d'ou celle que vous et Mr. Leibnits m'avez resoluë¹⁹⁾ se tirent facilement, avec plusieurs autres. C'est par elle aussi que je suis venu à bout de la quadrature assez remarquable de la courbe dont l'equation est x³+y³ ∞ xyn²⁰⁾, que Mr. des Cartes, dans sa lettre 65^e du 3^e volume²¹⁾, et nostre Mr. Hudde ont considerée pour autre chose²²⁾ Mr. Des Cartes en parle comme si elle avoit plusieurs feuilles²³⁾, quoy qu'elle n'en ait qu'une, comme dans cette figure est ABCH, son trait continuant en AK, AL, le long de l'asymptote EFG, perpendiculaire au diametre CA, prolongé d'un tiers AF. Je trouve le contenu de la feuille ABCH égal à ⅙ nn ou ⅓ du quarré du diametre AC²⁴⁾; et l'espace infini des deux costez entre AK, AL et l'asymptote, encore de la mesme grandeur²⁵⁾. On ne s'imagineroit pas que cette

15) Voir l'Appendice IV à cette lettre, la pièce N^o. 2781.

16) Voir la pièce N^o. 2780, les § VII et VIII de la pièce N^o. 2781 et la pièce N^o. 2782.

17) Voir, pour un exemple, le dernier alinéa du § IX de la pièce N^o. 2781.

18) C'est-à-dire la quadrature de l'aire FLM de la première figure de la présente lettre. Consultez sur cette quadrature la pièce N^o. 2780, surtout la note 1 de cette pièce.

19) Il s'agit de la quadrature de la courbe aaxx=aayy-y⁴ mentionnée par Leibniz dans sa lettre N^o. 2664 (à la page 51) et par de l'Hospital dans sa lettre N^o. 2775, où l'équation de la courbe est mise sous la forme analogue: a²y²-2y⁴=2a²x². Sur la dérivation de cette quadrature au moyen de la méthode de Fermat on peut consulter le § VII de la pièce N^o. 2781.

20) Voir sur cette quadrature l'Appendice V à cette lettre, notre pièce N^o. 2782.

21) Il s'agit de sa lettre à Mersenne du 23 août 1638, reproduite par Charles Adam et Pau Tannery dans l'édition récente des ‘OEuvres de Descartes’ sous le N^o. CXXXVIII du Tome II (voir les pages 313-316). Descartes s'y occupe de la détermination de la tangente et de ‘la plus grande largeur’ de la boucle dans la direction perpendiculaire à l'axe AC. (Voir la figure de la page suivante).

22) On rencontre les considérations de Hudde, qui se rapportent encore à la détermination de la plus grande largeur, aux pages 493 et 497-499 des ‘Exercitationes mathematicae’ de van Schooten, ouvrage que nous avons cité dans la Lettre N^o. 128, note 3.

23) On peut consulter sur cette circonstance une note que l'on rencontre à la page 341 du Tome II de l'édition des ‘OEuvres de Descartes’ mentionnée dans la note 21.

24) Voir le § I de la pièce N^o. 2782.

25) Voir le § III de la pièce N^o. 2782.

[p. 352]

courbe dust avoir une quadrature si reguliere et si simple. Celle qui est generale pour les segments l'estant de mesme, qui s'exprime par un seul terme²⁶⁾.

La question de la courbe de Mr. de Beaune²⁷⁾, que propose M. des Cartes dans sa lettre 79^e du 3^e vol. ne tombe point dans la regle de M. Fatio ni dans celle dont m'a fait part Mr. Leibnits. C'est pourquoy je seray bien aise de voir quelle courbe vous avez trouvè pour la soutangente donnée yy-xy/a. Je crois de mesme bien difficiles à trouver celles qui ont les soutangentes que vous marquez 2y³/yy+2yx-xx et √ay+xx, qui sont aussi hors de ces regles. Mais sur tout je souhaite de voir de quelle espece est la derniere des deux. Apparemment elle est transcendente, dont la construction suppose quelque quadrature, comme celle qui a pour soutangente aa/√aa-xx demande les quadratures du cercle et de l'hyperbole²⁸⁾. J'avoue que je ne vois pas encore par quelle adresse on pourra developper ces courbes qui respondent à vos soutangentes, si ce n'est peut estre par quelque converse de la regle des tangentes de Mr. de Roberval²⁹⁾, dont l'usage s'etend plus loin que peut-estre l'autheur n'a scu. Mais je ne veux pas me donner la peine de chercher, esperant de l'apprendre de vous ou de Mr. Newton.

Voicy encore deux exemples de soutangentes, par ce que vous en demandez, ou les regles que je connois ne reussissent point;^a) aay+xyy/ax-xy-ay et

26) Voir, pour la valeur du segment, qui est égal à ⅙nx²:y pour AD=x, BD=y, AC=½n√2, les § II et III de la pièce N^o. 2782.

27) Voir, sur ce problème, la Lettre N^o. 2765.

28) Voir la Lettre N^o. 2735, note 18.

29) Probablement la méthode bien connue de de Roberval, communiquée en 1668 à l'Académie des Sciences et publiée en 1693 dans les ‘Divers ouvrages de Mathématique et de Physique’ (voir la Lettre N^o. 2432, note 1) sous le titre: ‘Observations sur la composition des mouvements, et sur le moyen de trouver les touchantes des lignes courbes’.

a) hyperbole aa ∞ ax-ay [Christiaan Huygens].

[p. 353]

^b) x³y/3x³+3aay-2xyy³⁰⁾, qui semblent estre du genre dont est la premiere de vos deux precedentes et peut-estre celle de la courbe de Mr. de Beaune.

Je vois que Mr. des Cartes fait mention³¹⁾ de la solution³²⁾ qu'il auroit envoiée pour cette ligne, mais je doute si elle aura estè meilleure que celle qu'il donne pour la logarithmique³³⁾. S'il revenoit au monde il trouveroit la geometrie bien augmentée.

b) 0 ∞ x³-xxy+aay [Christiaan Huygens].

30) D'après la page 156 du livre H, cette dernière expression représente la soustangente ydx/dy=x²y-a²y/3x²-2xy de la courbe x³-x²y+a²y=0 ‘déguisée’ au moyen de la substitution x²=x³y^-1+a², appliquée au numérateur et au dénominateur; comparez la note b) de Huygens. De même la note a) indique l'hyperbole aa=ax-xy comme la courbe dont la première expression a été déduite. On peut consulter d'ailleurs, sur la solution générale des équations différentielles auxquelles ces expressions pour la soustangente donnent lieu, une des notes de la lettre de de l'Hospital à Huygens du 12 mai 1693.

31) Dans sa lettre de 1645, citée dans la note 4 de la Lettre N^o. 2765, où il s'exprime comme il suit: ‘Cette question [le problème de de Beaune] me fut proposée, il y a cinq ou six ans, par Monsieur de Beaune, qui la proposa aussi aux plus célèbres Mathematiciens de Paris et de Thoulouze; mais je ne sçache point qu'aucun d'eux luy en ait donné la solution, ny aussi qu'il leur ait fait voir celle que je luy ai envoyée’.

32) La solution fut envoyée à de Beaune dans une lettre du 20 février 1639, qui constitue le N^o. CLVI du Tome II de la correspondance de Descartes publiée par Adam et Tannery (voir les pages 514-517 et les annotations des éditeurs aux pages 520-523). Cette lettre était accessible à Huygens dans l'édition de Clerselier où elle paraît comme le N^o. 71 du Tome III, et sans doute il en avait pris connaissance autrefois (voir encore la note suivante); mais il semble qu'il n'y aît pas reconnu alors une solution du problème de de Beaune, lequel problème, en effet, n'y est pas mentionné expressément.

33) Il est presque certain que Huygens a ici en vue la construction de la courbe elle-même, qui constituait la solution du problème de de Beaune, mentionnée dans la note précédente. Voici comment Descartes s'exprime sur la courbe en question:




‘En la deuxième AVX [de vos trois lignes courbes], dont le sommet est A, au lien de considerer l'axe AY avec son ordonnée XY, j'ay consideré l'asymptote BC, vers laquelle ayant mené des ordonnées paralleles à l'axe, comme PV, RX, &c., et des tangentes comme AC, ZVN, GXM, &c., j'ay trouvé que la partie de l'asymptote qui est entre l'ordonnée et la tangente d'un mesme point, comme PN, ou RM, &c. est tousiours égale à BC, ainsi que vous verrez facilement par le calcul’. Après quoi il procède à donner une construction approchée de la courbe AVX.
Or Huygens aura reconnu sans doute qu'on n'avait qu'à ‘perpendiculariser’ pour ainsi dire les ordonnées PV, RX pour transsormer cette courbe dans la ‘logarithmique’ à soustangente constante dont il s'était tant occupé.

[p. 354]

Le probleme du Sr. Viviani³⁴⁾ n'avoit pas grande difficultè et il avoit aussi estè resolu d'abord par Mr. Leibnits, et en suite sur le mesme fondement par Mr. Bernouilli, qui adjoute cette jolie remarque qu'en cheminant sur la Terre en sorte qu'on avance egalement en longitude et latitude, on decrit une ligne qui resout ce probleme. Et c'est cette ligne qui est egale à celle d'une Ellipse, comme on peut demontrer assez facilement³⁵⁾.

Un scavant Anglois vient de me dire que la seconde edition des Principes de Mr. Newton, de la quelle Mr. Fatio devoit avoir soin, ne se fera pas encore si-tost. Il y a une infinité de fautes à corriger³⁶⁾ et quelques unes qui sont de l'autheur, comme il reconnoit luy mesme³⁷⁾. J'estime beaucoup son scavoir et sa subtilitè, mais il y en a bien de mal emploiè à mon avis, dans une grande partie de cet ouvrage lors que l'autheur recherche des choses peu utiles, ou qu'il batit sur le principe peu vraisemblable de l'attraction³⁸⁾. Le mesme Anglois m'apprend, qu'on imprime, ou qu'on a desia imprimè la methode de Mr. Newton pour le Probleme renversè des Tangentes, qu'on l'a joint au livre de Wallis de Algebra, qu'il a donnè cy-devant en Anglois et qui est maintenant traduit en Latin et augmentè³⁹⁾. L'Hypothese de Mr. Fatio⁴⁰⁾ dans son traitè de la Pesanteur ressembloit à celle de M. Varignon⁴¹⁾, et souffroit la mesme difficultè, qui est l'accumulation necessaire de la matiere autour du centre vers lequel selon eux elle pousse les corps. Laquelle difficultè Mr. Varignon ne resout point, et M. Fatio a besoin pour cela d'une hypothese fort estrange et peu concevable. Lors qu'il partit d'icy pour l'Angleterre il se plaignoit qu'il avoit perdu ce traité⁴²⁾. On trouve si peu d'occasion d'appliquer la geometrie à la physique, que souvent je m'en estonne. Et quand on en trouve il est difficile de le faire avec justesse. Cependant c'est ce qui merite le plus, avec les inventions de mechanique, qu'on s'y occupe, car autrement calculis ludimus, in supervacuis subtilitas teritur, comme dit quelque part Seneque.

34) Voir la Lettre N^o. 2768, note 17, et la pièce N^o. 2771.

35) Voir la pièce N^o. 2771, vers la fin.

36) Voir la pièce N^o. 2698.

37) Voir la Lettre N^o. 2732, note 10.

38) Consultez, à propos de cette opinion de Huygens sur l'hypothèse fondamentale de la théorie de l'attraction, celle que ‘toutes les petites parties, qu'on peut imaginer dans deux ou plusieurs differents corps, s'attirent ou tendent à s'approcher mutuellement’, la Lettre N^o. 2558, note 6.

39) Voir, sur ces éditions du livre de Wallis, la Lettre N^o. 2660, note 3. Sans doute il s'agit ici de l'exposé de la méthode de Newton des fluxions donné par Wallis, et qui fut publié pour la première fois dans l'édition latine de 1693 aux pages 390-396 du Chapitre 95.

40) Voir les Lettres N^os. 2570 et 2582.

41) Voir la Lettre N^o. 2677, note 11.

42) Voir la Lettre N^o. 2739.

[p. 355]

A propos de mechanique il a passé icy un François il y a quelque temps, qui montroit pour de l'argent une teste, construite en sorte qu'elle prononçoit quelques paroles. Je n'en fus averti, qu'apres son depart; peut-estre, Monsieur, en scaurez vous quelque chose. L'on m'a envoiè de Paris un certain imprimè, qui parle d'une invention du Sr. de Hautefeuille⁴³⁾, par la quelle il pretend que les pendules de poche ont receu une plus grande perfection. Il faudra voir ce que c'est, mais je connois a peu pres le talent et le genie du personnage. Il y a fort longtemps que je n'ay point ouy parler de Mr. le Duc de Roanes⁴⁴⁾. J'ay peur qu'il ne se souviene plus de moy. Si ce n'estoit pas prendre trop de libertè, je vous supplierois, Monsieur, de l'assurer de mes Respects et que je luy suis comme à vous etc.

Monsieur

Vostre treshumble et tresobeissant serviteur

43) Voir, sur de Hautefeuille, la Lettre N^o. 2023, note 3. Nous ne connaissons pas l'écrit mentionné dans la lettre. D'après un ‘Avis sur le privilège des horloges et des montres de la Nouvelle Invention’ publié sans date chez la Veuve Daniel Horthemels (4 pages in-4^o.), le Roi aurait accordé à de Hautefeuille, le 26 mars 1693, un privilège pour des horloges et montres d'une nouvelle invention. Il est cependant impossible de déduire du fatras, qui remplit cet avis, en quoi cette invention a consisté. Consultez encore la lettre de de l'Hospital à Huygens du 12 mai 1693 et celle de Huygens du 23 juillet 1693.

44) Consultez, sur Arthus Gouffier, duc de Roanez, la Lettre N^o. 837, note 1.