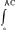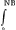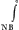Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 364]

N^o 2781.
Christiaan Huygens.
[octobre 1692]. Appendice IV¹⁾ au No. 2777.

La pièce se trouve à Leiden, coll. Huygens.

1) Cet Appendice, emprunté aux pages 110, 111, 138-140 du livre H, contient les démonstrations des théorèmes qui servent de fondement à la méthode de Fermat, de laquelle il est question dans la Lettre N^o. 2777, et en outre quelques applications de cette méthode. Il a été reproduit dans un autre arrangement par Uylenbroek, Exercitationes, Fasc. II, p. 145-154.

§ I²⁾.

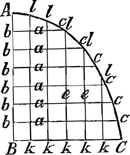Fig. 1.

Particulae aequales in AB aequales sunt singulis particulis aequalibus in BC. Singulae BC, bc vocentur a³⁾; singulae LK, lk vocentur e; significat summam.

Constat jam summam omnium a aequari summae omnium e⁴⁾; quia ductae in unam particulam rectae AB vel BC, faciunt aream figurae ABC.

Summa ▭^orum kl. kB sive rectarum e in distantias suas ab AB, aequaliter crescentes, quae sunt a, est aequalis ½ summae qu^orum ab rectis cb quae dividunt AB in partes aequales. Ratio intelligitur ex ungula 45 gr. super fig. ABC abscissa per AB, quia ungula haec secta planis ad figuram rectis, secundum lineas lk facit ^m ▭ orum kl. kB. Eadem vero secta planis ad figuram rectis, secundum lineas bc, facit ½ qu^orum ex bc sive a utrimque nempe omnia ducta intelligenda in unam particularum BC vel AB rectarum⁵⁾. Itaque ae=½ aa.

2) Démonstration du théorème ∫xydx=½ ∫x²dy (en valeur absolue), où les intégr ations doivent être exécutées le long d'une courbe qui s'étend d'un point A sur l'axe des-y à un point C sur l'axe des-x.

3) C'est la notation de Fermat, qui emploie les voyelles pour désigner les quantités variables et les consonnes pour les quantités constantes.

4) En notation moderne ∫xdy=∫ydx.

5) C'est-à-dire en multipliant la première somme par une des particules kk et la seconde par bb où kk=bb.

[p. 365]

§ II⁶⁾.

a	e
½ a brachia rectarum a super AB	a brachia rectarum b super AB
_____	_____
½ aa.	ae.

6) Autre démonstration du même théorème. (Le moment de l'aire ABC sur AB est calculé de deux manières différentes).

§ III⁷⁾.

½ aa semiquadrata super applicatis seu trianguli quorum anguli 45 gr. sunt ad AB.	ae rectang. ae seu Bk, kl erectam super lk.
⅔ a brachia istorum triangulorum super AB.	a brachium rectangulorum ae super AB.
_____	_____
⅓ a^3.	aae.

⅓ a^3= aae.

7) Démonstration du théorème ⅓∫x³dy=∫x²ydx. (Le moment, sur un plan vertical passant par AB, de l' ‘ungula’ du § I est calculé de deux manières différentes).

§ IV⁸⁾.

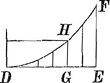Fig. 2.

Hic super omnibus applicatis BC sive a residua parabolica ejusdem omnia parabolae, qualia sunt DEF, DGH, etc. intelligenda sunt, quae sunt inter se ut cubi rectarum a seu applicatarum⁹⁾. Quae residua in sua brachia ducta hoc est in ¾ a, facient producta in ratione quadratoquadratorum super a. Summa

8) Démonstration du théorème ∫x⁴dy=4∫x³ydx. (Le moment sur un plan vertical passant par AB du volume engendré par les paraboles z=y²:r est calculé de deux manières différentes).

9) C'est-à-dire leurs aires DEF, DGH.

[p. 366]

vero istorum productorum erit eadem ac eorum quae fiunt ex rectangulis HG in kl, seu l, ductis in sua brachia a. Sunt autem HG=aa/r; residua ut DHG sunt ⅓ ▭ HD hoc est ⅓ a³/r.

⅓ a^3/r [residuum HDG].	aa/r [recta HG]
¾ a [brachium super AB].	e [recta kl]
	_____
_____	aae/r [rectang. HG kl]
¼ a^4/r	a [brachium super AB]
	_____
	a^3e/r

¼ a^4/r= a^3e/r; a^4= 4a^3e^10).

10) Il est clair que le même procédé pourrait servir pour la formule générale ∫x^m dy=m∫x^m-1 ydx, les aires es les centres de gravité des paraboles z=y^m-2:r^m-3 étant connus.

§ V¹¹⁾.

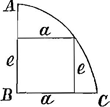Fig. 3.

Oportet a vel e [fig. 3] ab angulo recto B accipi ut theoremata ista locum habeant (cum vero aliter accipiuntur, vide quid eveniat in exemplo extremae paginae hujus¹²⁾, quae sic quoque vera sunt si curva CA in infinitum abeat secundum asymptoton BA, sed ita ut spatium tamen infinitum CAB aequetur certo spatio, sive ut quantumlibet prope ad certi spatij mensuram accedat.

11) Quelques remarques supplémentaires.

12) Voir le premier exemple du § VI.

[p. 367]

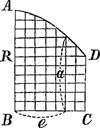Fig. 4.

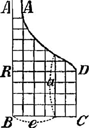Fig. 5.

Potest quoque curva solum incipere in D, ut DC [fig. 4] sit recta linea, DA curva, et tunc DC minima omnium a.

Potest etiam et infinita extensio esse curvae DA [fig. 5], et simul DC recta linea.

Attamen e quae in aequatione sunt tantum quae ex curva DA applicantur ad RA. Et e quae in ▭ DB vocantur E.

§ VI¹³⁾.

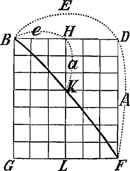Fig. 6.

BF [fig. 6] curva. BH=e; HK=a; BD sive GF=E maxima omnium e; DF=A maxima omnium a.

Hic summa omnium eea, hoc est solidorum ex omnibus a in quadrata distantiarum suarum à BG, erit aequalis

⅓ E^3-⅓ e^3.

BD et BG in particulas utrimque aequales divisae intelliguntur; jamque in eea, e significant distantias ipsarum HK seu a à BG aequaliter crescentes; at in e³, e significat rectas à curva BF applicatas ad BG, eamque in dictas particulas aequales iis quae in BD, dividentes; denique in E³, E significat rectas quarum singulae aequales GF sive BD, maximae omnium e, quaeque sunt ipsae e usque ad DF productae. Demonstratio. Quum omnium KL in quadrata distantiae suae e², aequetur ⅓ cuborum applicatarum e, quae BG in particulas aequales dividere intelliguntur, sitque omnium HL, ipsi DF seu maximae a aequalium, in quadrata distantiarum e², aequalis ⅓ cuborum ex omnibus E, sequitur omnium HK in qu. distantiarum suarum ee aequari ⅓ E³-⅓ e³¹⁴⁾.

13) Extension des théorèmes de Fermat à quelques cas où la courbe ne s'étend pas d'un point de l'axe des y à un point de l'axe des x (c'est-à-dire où les termes x₂y₂^m et x₁y₁^m de l'équation mentionnée dans la note 14 de la Lettre N^o. 2777 ne s'annulent pas).

14) Pour E³ on pourra écrire: AE³; pour e³: ∫x³dy, si BH=x, HK=y. On a donc en langage moderne ∫xy²dx=⅓AE³-⅓∫x³dy; relation correcte.

[p. 368]

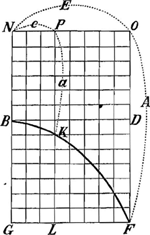Fig. 7.

BF [fig. 7] curva NP=e; PK=a; NO=E; OF=A.

Rectae a sunt à curva BF applicatae ad NO, eamque in particulas aequales dividentes.

Etiam hic aee=⅓ E³-⅓ e³¹⁵⁾.

Sed E in E³ significant e maximas per totum ▭NF applicatas ad NG, eamque in particulas aequales tum inter se, tum rectam NO dividentes.

e vero in e³ rursus applicatas à curva BF ad BG, eamque in particulas dictis aequales dividentes.

Item e in aee significat rursus distantias linearum PK ab recta NG aequaliter per particulas crescentes.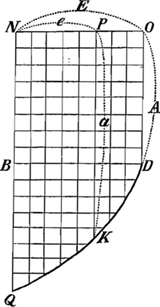

Fig. 8.

DQ [fig. 8] curva; NP=e; PK=a;

NO=E; OD=A minima omnium a.

Hic aee= ⅓E³+⅓ e³¹⁶⁾; ut E in E³ significet e maximas per ▭ ND applicatas ad NB.

e in e³ rursus applicatas à curva DQ ad rectam BQ, eamque in aequales part. dividentes.

At e in aee ut pridus significat distantias rectarum a ab NQ.

15) En posant NP=x, PK=y, on arrive à la relation de la note précédente.

16) En parcourant la courbe dans la direction de Q à D on a, en notation moderne, ∫x²ydx==⅓ AE³-⅓∫x³dy, mais, puisque les accroissements dy de PK sont alors négatifs, on doit remplacer -⅓∫x³dy par ⅓ e³, ce qui amène la relation obtenue par Huygens.

[p. 369]

§ VII¹⁷⁾.

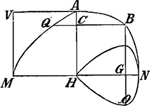Fig. 9.

Consideretur primo AH [fig. 9] divisa in partes minimas aequales, tunc singula quadrata ramorum BC applicata rectae AH vel ipsi aequali AV, vel alij lineae si velimus, faciunt rectas CQ, quae hic cadunt in parabolam AM, cujus vertex M, axis MH. Haec ex calculo ad א¹⁸⁾.

Deinde consideretur HN divisa in partes aequales ijs in quas secta fuit AH, nec referret si non exacte explerent HN, uti nunc faciunt quia ABN ponitur quadrans circuli.

Jam omnia simul rectangula ex BG in GH bis sumpta, aequari scimus omnibus quadratis CB (vide pag. 110¹⁹⁾, ac proinde omnia simul rectangula BG in GH erunt aequalia ½ omnium quadratorum BC. Quare etiam omnia rectangula BG in GH si applicentur ad eandem AH aut aliam rectam, ad quam applicata fuerunt quadrata BC (ex qua applicatione hic natae sunt rectae GO, faciendo ut AH ad HG ita BG ad GO) erunt necessario omnes simul GO aequales dimidio omnium simul CQ, quae ex applicatione totorum quadratorum BC ad AH ortae erant; atque ita figura HON hic ½ parabolae AMH, sive ⅓ quadrati ex AH²⁰⁾.

Hoc est fundamentum eorum quae habet Fermatius in libro de aequationum localium transmutatione pag. 51, 52 &c.²¹⁾; quae ibi confuse perverse et nulla addita demonstratione proponuntur, et plena praeterea sunt sphalmatis typographicis.

17) Première application. Quadrature de la courbe x⁴-a²x²+a²y²=0.

18) Il ne semble pas nécessaire de reproduire ce calcul puisqu'on trouve immédiatement QC=BC²:AH=(AH²-HC²):AH=AH-HC²:AH.

19) Voir le théorème du § I de la présente pièce.

20) Ainsi la quadrature est trouvée de la courbe GO=y=HG × BG: AH=x√a²-x²: a, ou bien: x⁴-a²x²+a²y²=0, sur laquelle Huygens remarque encore: ‘quadrabilis, 5^ta Huyghenij, vide pag. 19. (Voir la note 2 de la Lettre N^o. 2735). Ejusdem generis cujus mea pag. 1 lib. G. [voir le § I de la pièce N^o. 2612] nec tamen prorsus eadem. Ergo apud Fermatium potuit hujus quadraturam invenisse Leibn.’ On rencontre cette quadrature de Leibniz à la page 51 de la Lettre N^o. 2664.

21) Voir la note 14 de la Lettre N^o. 2777. Remarquons encore que plusieurs des erreurs typographiques assez embarrassantes qu'on rencontre dans l'édition originale ne se retrouvent plus dans l'édition récente de Tannery et Henry, où en outre la figure de la page 51 (page 271 de l'édition récente), a été améliorée par l'addition de la courbe HONH.

[p. 370]

§ VIII²²⁾.

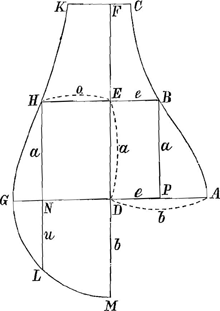Fig. 10.

Ad pag. 54 operum Fermatij²³⁾.

Aequatio curvae CBA [fig. 10] b³=aae++bbe.

Sit oo=be; fit nova curva KHG in qua applicatae o sunt mediae proportionales inter b et e; dabiturque summa omnium e si detur summa quadratorum oo.

oo/b=e; fit b³=aaoo/b+bboo/b; b⁴=aaoo++bboo aequatio curvae KHG.

Sit jam ao=bu²⁴⁾; fit b⁴=bbuu+bboo; bb-oo=uu aequatio curvae GLM, quae est circ. circonf.^a Ergo omnia o habentur quad^ra circuli.

Nam summam quad.^orum oo scimus aequari duplae summae rectangulorum oa²⁵⁾. Ergo et duplae summae rectang.^orum bu, quia bu=oa. Si ergo applicentur omnia qu^a oo ad b, itemque applicentur omnia rectangula bu ad b, fient lineae quarum summa priorum oo/b sive e, erit dupla summae posteriorum, quae sunt u. Atqui omnes e faciunt spatium infinitum CBADEF, si nempe ductae intelligantur in unam particularum aequalium in quae DF infinita secta est a rectis e. Omnes item u faciunt quadrantem circuli DGM, ductae nempe in unam particularum aequalium in quas secta est DG à rectis u, quae particulae prioribus aequales ponuntur. Est ergo spatium infinitum CBADEF duplum quadrantis DGM. Adeoque quadratura ejus pendet a quadratura circuli.

22) Deuxième application. Quadrature de la courbe xy²+a²x-a³=0.

23) Ici, comme dans les autres exemples, Huygens a suivi les indications de Fermat; mais de manière à obtenir des résultats mieux précisés. La page 54 citée correspond à la page 279 de l'édition récente.

24) En guise d'explication Huygens ajoute ‘pono ao=bu quia si inveniam omnia u habebo omnia ao, ideoque et omnia oo quia haec=bis omnia ao, Habebo autem omnia u positâ quadratura circuli’.

25) Par l'application du théorème du § I de cette pièce, la courbe GHK étant supposée s'étendre jusqu'à l'infini.

[p. 371]

Dico et spatium BPA esse duplum spatii GNL. Sunt enim omnia qu.^a oo solidi EHDG ad omnia quadrata partium o in rectangulo EN, sicut omnes e in spatio BADE ad omnes partes linearum e in rectangulo BD. Itaque solidum ex EHGD circa ED est ad cylindrum ex ▭^o EN circa eandem ED, ut spatium EBAD ad ▭ BD. Et dividendo, solidum ex EHGD ad solidum ex HNG circa eandem ED, ut spatium EBAD ad spatium BPA. Sed solidum infinitum ex KGDF est ad solidum ex EHGD, ut spatium inf.^m FDAC ad spat. EBAD. Ergo solid. infin. ex EHGD²⁶⁾ ad solidum ex HGN ut spat. inf. FDAC ad spat. BPA. Sed solidum inf. ex KGDF est ad solid. ex HGN ut omnia ao in spatio inf.^o KGDF ad omnia ao in spatio HGN, hoc est ut omnes u in spatio DMG ad omnes u in spatio LGN. Ergo ut quadrans DMG ad portionem LNG ita spat. inf. FDAC ad spat. BPA etc.

KHG curva est ea quae nostra auxiliatrix ad construendum catenariam²⁷⁾.

26) Lisez KGDF.

27) En effet, l'équation b⁴=aaoo+bboo peut être identifiée avec celle de la courbe xxyy==a⁴-aayy, mentionnée entre autres dans la pièce N^o. 2624.

§ IX²⁸⁾.

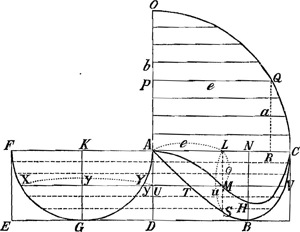Fig. 11.

Ad pag. 55 et 56, Fermatij²⁹⁾.

Aequatio curvae OC [fig. 11] datur bb-aa=ee, quae est circuli circonf.^a PQ sunt e, PA vel QR sunt a. AO rad.=b. Quaeritur summa cuborum e.

Si haberem summam omnium aee, haberem et summam omnium e³, quia eea=⅓ e³³⁰⁾.

Sit bbo=aee, unde bbo/ee=

28) Quatrième application. Détermination de l'intégrale ∫x³dy, étendue à un quart de cercle. Pour une cinquième application, se rapportant à la quadrature du ‘folium’ de Descartes, nous renvoyons à la pièce N^o. 2782.

29) Voir les pages 281 et 282 de l'édition récente de Tannery et Henry.

30) Voir le § III de cette pièce.

[p. 372]

=a et o=aee/bb. Hinc curvam secundam construo AHC, in qua AL sunt e, LM sunt o; cujus curvae aequatio fit, substituto in aequ.^e valore a, bb-b⁴oo/e⁴=ee, sive bbe⁴-b⁴oo=e⁶.

In hac curva jam sciri deberet summa omnium o.

Sit eu=bo. Si jam eu haberem, etiam bo haberem, ideoque o; fit autem nunc curva bbe⁴-e⁶=bbeeuu sive bbee-e⁴=bbuu quam construo ex eo quod u=bo/e: sumtis e ut ante in AC aequalibus. Est autem haec curva ABC (LA=e, LS=u) eadem quae in Exemplo pag. 138³¹⁾; ut patet ex aequatione. In hac curva si haberem summam omnium e qu. (quae rectam AD aequaliter secare jam debent) in spatio ABD, itemque e qu. quae in spatio ADBC, haberem et eorum differentiam, quae aequalis est omnibus³²⁾ eu; unde bo haberem³³⁾.

Pono ee=by, unde y=ee/b et hinc quartam curvam invenio AGF quae est circuli circonf.^a34).

Ergo³⁵⁾ quia singula by sunt=ee erit summa ee ad summam differentiarum ee ut summa by ad differentiarum by, hoc est ut ▭ AE ad semicirculum AGF. Et summa ee ad dimidiam summam differentiarum ee ut summa by, hoc est ut ▭

31) Voir le § VII de cette pièce.

32) Lisez: ‘duplo omnium’.

33) On a en effet: eu de=-½e²du-½e²du=½VU²du-½TU²du. Huygens d'ailleursajoute la justification qui suit: ‘Non enim hic omnia e qu.= 2eu, sed differentia quâ omnia quad.a rectarum e quae sunt in spatio CBDA superant omnia qu.a rectarum e quae sunt in spatio BAD, est aequalis 2 eu. Omnia eu est solidum ex figura ABC circa AD [il s'agit du cylindre sur ABC coupé par un plan partant de AD sous un angle de 45^o]; hoc autem habetur aeq. dimidio ex omnibus e qu.^is; hoc est ex solidis ex ABD et ACBD circa AD. Est enim horum differentia, hoc est summarum omnium dimidiorum quad.^orum ee.’

34) Puisque, d'après un petit calcul en marge, la substitution de ee=by dans l'équation bbee--e⁴=bbuu de la troisième courbe, amène l'équation b³y-bbyy=bbuu ou bien by-yy=uu.

35) Le raisonnement qui va suivre, semble embarrassant et compliqué plus que nécessaire, puisqu'il suffit de remarquer qu'on a, d'après ce qui précède, eu=½UV²-½ UT²==½b XU-½b YU=½b aire FGA=b aire KGA; résultat consigné dans l'alinéa suivant.

[p. 373]

AE in altitudinem b ad dimidiam summam differentiarum by, hoc est ad quadrantem KGA in altitudinem b³⁶⁾.

Ergo quadrans KGA in altitudinem b erit aequalis summae omnium e in u.

Ergo et summae omnium bo, quia aequalia posuimus eu=bo.

Ergo spatium AHC=quadranti KGA; quod Notandum³⁷⁾.

Sed [] bbo erat=[] aee=⅓[]e³. Ergo quadrans KGA in altitudinem b, insuper ductus denuo in b, aequabitur ⅓[]e³. Hinc vero invenitur centrum gravitatis ungulae super quadrante AOC abscissae per AO ang.^o semirecto, oportet enim eam in brachium suum super AO ductam aequari omnibus semiquadratis super lineas e in ungula existentibus ductis in sua brachia super AO, hoc est in ⅔e, unde oritur ⅓[]e³ pro producto ungulae dictae in brachium suum. Erat autem et solidum ex quadrante KGA in b ductum []⅓e³. Itaque solidum hoc suspensum in puncto C brachij CA aequiponderat sive aequalem gravitatis momentum habet super recta AO, ac ungula ante dicta. Quare ut ungula ad solidum illud, ita b ad brachium ungulae super AO. Est autem ungula=⅓b³ ut aliunde notum, et solidum dictum=¼bbq, si arcus GA sit q: nam KA=½b. Itaque eorum ratio quae 4b ad 3q. Ergo ut 4b ad 3q ita b ad ¾q, quae erit longitudo brachij ungulae in rectam OA, quod et aliunde scimus³⁸⁾ ita se habere.

36) On lit encore en marge: ‘Nota hic ad summam omnium ee inveniendam in curva ABC, debuisse duci istas e ita ut rectam AD in partes aequales dividerent; neque aliter ad curvam ABC alia statui poterat ad rectam AD, in qua y essent ut ee. Ex duabus autem e quae sunt UT, UV, fiunt duae y quae sunt UY, UX’.

37) On connaît donc de cette manière la quadrature de la boucle formée par la courbe y²=(a²-x²)x⁴:a⁴.

38) Sans doute à l'occasion de la détermination du centre d'oscillation d'un secteur de cercle. Comparez la Propositio XXI de l' ‘Horologium Oscillatorium’, Pars Quarta, d'après laquelle la détermination du centre d'oscillation de la figure plane AOC, oscillant autour de l'axe OA, dépend de celle du centre de gravité de l' ‘ungula’ en question, et consultez en particulier le sous-article de cette proposition intitulé: ‘Centrum oscillationis Sectoris circuli’. En effet, la longueur ¾q du ‘brachium ungulae’ n'est autre que la distance du centre d'oscillation de la figure AOC à l'axe AO.