Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 361]

N^o 2780.
Christiaan Huygens.
18 décembre 1692.
Appendice III¹⁾ au No. 2777.

La pièce se trouve à Leiden, coll. Huygens.

1) Cet Appendice, emprunté à la page 155 du livre H, où il est daté par Huygens du 18 décembre 1692, et que nous avons divisé en deux paragraphes, contient une construction simplifiée pour la quadrature de l'aire FLM de la figure 1 de la Lettre N^o. 2777. Il est précédé à la page 154 de quelques recherches infructueuses pour arriver à cette quadrature par d'autres méthodes. Dans ces recherches préliminaires, Huygens commence par réduire le problème, au moyen du théorème de Barrow, à celui de trouver la courbe dont la soustangente (ydx/dy) égale y²(a²-x²)/2aax, c'est-à-dire à l'équation différentielle 2aaxdx-y(a²-x²)dy=0. Alors naturellement, la méthode de Leibniz de la séparation des variables ramène la quadrature qu'il s'agit de trouver, et celle de Fatio ne réussit pas non plus. ‘Hic vero nec Fatij methodus succedit, nec mirum, quia per eam non nisi geometrica inveniri posset curva LO (la courbe à soustangente donnée), atque ita absolute quadraretur spatium NHM (lisez FLM); quod fieri non potest, cum a quadratura Hyperbolae ejus dimensio pendeat, ut invenit Hospitalius’. Et Huygens ajoute ‘...haec omnia nihil juvant. Ergo pag. sequenti methodum Fermatii experiamur’, c'est-à-dire la méthode mentionnée dans la Lettre N^o. 2777.

§ I²⁾.

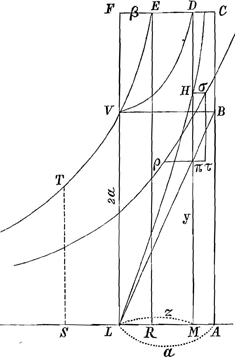2aaz/aa-zz=y, MH.

Aequatio Curvae LH:

zzy+2aaz=aay; sit ωz/a=y

zzzω/a+2aaz=aωz

zzω+2a^3=aaω

zz=aaω-2a^3/ω; 2a^3/aa-zz=ω [MD]

Ergo ω sunt erectae in spatio VDML, quod potest quoque ad quadraturam hyperbolae reduci³⁾. Sed hic nihil opus est.

Sit zz=aβ; zz/a=β, FE.

aβ=aaω-2a^3/ω

ωβ+2aa=aω

2aa=aω-βω.

2) Réduction de la quadrature de l'aire LHM à celle de l'hyperbole.

3) Consultez la pièce N^o. 2661, où l'aire αλωγ de la figure 1 de cette pièce est réduite successivement à la somme d'une série infinie (au § I), à une aire hyperbolique (aux §§ II et III) et aux logarithmes (au § V, voir la note 37).
Or l'équation de la courbe λα:y=ηλ=a³/a²-x² ne diffère pas essentiellement de celle: ω=2a³/a²-z² de la courbe VD.

[p. 362]

β ergo est applicata in hyperbola ad perpend. asymptoto, FL; ωz=ay. Ergo si haberem ωz⁴⁾ haberem quoque ay⁵⁾ unde et y, hoc est quadraturam quaesitam. Haberem ωz si haberem zz⁶⁾ in spatio VDF. Quod sic ostenditur⁷⁾ ωz est ungula super spatio VDML abscissa per LVF angulo semirecto; cui ungulae aequatur ½ summa quadratorum ab rectis in rectangulo LFDM ad FL applicatis, minus ½ summa quadratorum ab applicatis ad FV in spatio curvilinea VDF.

Porro haec posterior ½ summa aequatur solido cujus basis est spatium hyperbolicum EVF altitudo=½ FC sive ½ a; quia ubique β=zz/a ideoquesingula ½ αβ==½ zz, nempe earum z quae sunt in spatio DVF applicatae ad FV.

Sed prior ½ summa quadratorum ab rectis in·▭ FDML, aequatur toti ▭^o EFLR ducto in altitudem ½ a, quia videlicet proportionales CF, DF, EF. Ergo differentia dictarum ½ summarum quadratorum aequabitur solido cujus basis spatium hyperb. EVLR, altitudo ½ a; quod igitur= ωz, hoc est ay; sive spatio LHM in a. Itaque cum spat. hyperbolicum VERL in ½ a sit= ωz= ay: Erit spat. LHM=½ sp. VERL.

4) Lisez: ∫ωzdz; ω=MD, z=LM.

5) Lisez: ∫aydz; y=MH.

6) Lisez: ∫zzdω.

7) Le théorème qui précède constitue une application de la méthode de Fermat; mais Huygens fait suivre une démonstration indépendante.

§ II⁸⁾.

Si describeretur Logarithmica cujus subtangens AS=√2aa, quantum est latus quadrati in angulo hyperbolae TVE. ET ad illam applicarentur duae rectae

8) Déduction de la construction simplifiée à l'aide du résultat obtenu dans le paragraphe précédent.

[p. 363]

rationem habentes quam DM ad VL, hoc est quam ω ad 2a, vel quam MH ad 2LM, hoc est quam y ad 2z, istarum rectarum distantia in asymptoto Logarithmicae ducta in AS subtangentem, faceret rectangulum=spatio hyperbolico VERL⁹⁾ quod duplum esset spatii LHM. Si vero in logarithmica cujus subtangens LA sive a duae rectae in eadem dicta proportione statuantur ad asymptoton, earum distantia ducta in subtangentem AL, faciet rectangulum dimidium prioris, quia alterum illud rectangulum erit ad hoc in duplicata ratione laterum. Ergo posterius rectangulum fiet aequale spatio LHM. Hinc brevissima constructio.

Ductu enim tangente in L puncto curvae LH (sumpta nempe AB dupla LA¹⁰⁾) à puncto π ubi secat applicatum MH ducatur asymptoto parallela ad Logarithmicam ρσ cujus subtangens=LA, eique occurrat in ρ. Item à puncto H similis parallela occurrat Logarithmicae eadem in σ. Jam distantia [ρτ] duarum perpendicularium in asymptoton ex punctis ρ et σ ductarum cum recta LA faciet rectangulum aequale spatio LMH¹¹⁾.

Convenit cum quadratura Hospitalij¹²⁾ sed est brevior conctructio.

9) Voir la note 10 de la pièce N^o. 2779.

10) Comparez la Lettre N^o. 2775, à l'endroit où il est renvoyé à la note 5.

11) D'après ce qui précède, cette aire égale aalMH/2LM=aalMH/Mπ, d'où la construction se déduit très facilement.

12) Voir la Lettre N^o 2775, au lieu où se trouve la note 6.