Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 358]

N^o 2779.
Christiaan Huygens.
décembre 1692.
Appendice II¹⁾ au No. 2777.

La pièce se trouve à Leiden, coll. Huygens.

Problema Hospitalij simplicissima via resolvitur.

1) Cet Appendice contient la déduction de la solution définitive de Huygens du problème de la rectification de la logarithmique, telle qu'on la rencontre dans la Lettre N^o. 2777, et dans la pièce N^o. 2793, c'est-à-dire dans l'article publié dans l' ‘Histoire des ouvrages des Sçavans’ de Février 1693. Nous l'avons emprunté à la page 160 du livre H et divisé en paragraphes. Le premier paragraphe contient la réduction du problème à la quadrature de l'aire BHQN.

§ I.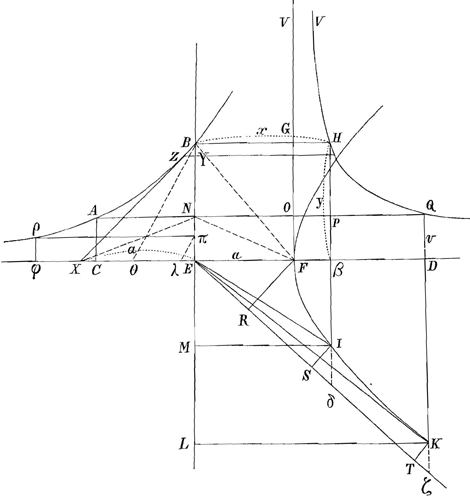

BA Logarithmica. VHQ curva pag. 108²⁾; asymptoti hujus sunt FD, FV.

Logarithmicae asymptotos DFC.

BA portio curvae aequanda rectae.

2) Voir la pièce N^o. 2778. On verra par la note suivante comment Huygens est parvenu ici à cette courbe, identique avec celle LQD de la pièce N^o. 2778.

[p. 359]

Si ut YB ad BZ, hoc est, ut EB ad BX ita sit BG=a ad BH cadit H in curvam VHQ³⁾, et erit recta NB ad curvam BA ut ▭ BGON ad spatium BHQN⁴⁾.

Quaerendum est spatium BHQN.

3) On peut considérer ce qui précède comme la définition de la courbe VHQ. Posant alors BH=x, Hβ=BE=y, XE=EF=a, on trouve facilement: y:√a²+y²=a:x, équation identique à celle de la pièce N^o. 2778, pour la courbe DL, en échangeant les x et y.

4) Puisque d'après la construction indiquée: Σa × BZ=ΣBH × BY.

§ II⁵⁾.

Spatium VQKFV infinitum est aequale spatio FKLE (vid. pag. 108⁶⁾ posita hyperbola aequilatera FK, centro E, semidiametro EF=a=subtangente logarithmicae BA.

Si utrinque auferatur spatium FDK, erit spatium infinitum VFDQV aequale spatio FKLE-spatio FDK; hoc est ▭^o DL-2 spatio FDK. Ergo sumptis horum dimidiis, erit Δ EKD-spat.^o FDK hoc est sector hyperbolicus FEK aequalis ½ spatii VFDQV.

Eadem ratione erit sector hyperb. FEI aequalis ½ spatii infiniti VFβHV.

Ergo spat. HβDQ=2 sector FEK-2 sector FEI; hoc est=2 spat. FRTK-2 spat. FRSI.

Ergo spat. HβDQ 2 spat. ISTK.

Sp. BHQN=▭ Bβ+sp. HβDQ-▭ ND vel ▭ Bβ+2 sp. ISTK--▭ ND=a√yy+aa-a √vv+aa+aq⁷⁾.

▭ BO=ay-av.

Ergo curva AB=√yy+aa-√vv+aa+q⁸⁾=XB-XN+q.

5) Réduction de la quadrature BHQN à celle d'un espace hyperbolique.

6) C'est-à-dire la pièce N^o. 2778. Voir le premier alinéa de cette pièce.

7) Ici v=QD, tandis que q représente provisoirement une ligne dont la longueur dépend de la quadrature de l'aire ISTK.

8) On a d'après le § précédent: NB: arc. BA=▭ BGON:BHQN, c'est-à-dire (y-v):arc. BA=a(y-v):a (√yy+aa-√vv+aa+q), d'où il suit facilement:arc. BA==√yy+aa-√vv+aa+q; tout va donc dépendre de la construction de la longueur q.

§ III⁹⁾.

Si super asymptoto logarithmicae cujus subtangens esset=ER=√½aa, applicarentur duae rectae in ratione SI ad TK, sive Iδ ad Kζ, earum intervallum

9) Construction de la longueur auxiliaire q.

[p. 360]

ductum in subtangentem faceret ▭ aequale spatio ISTK¹⁰⁾. Si vero in hac Logarithmica cujus subtang. a applicentur duae in eadem ratione illa earum intervallum ductum in a faciet ▭ aequ. duplo spatio ISTK hoc est aequ. spatio HQDβ¹¹⁾.

Eβ vel βδ-βI=Iδ

x-√xx-aa=Iδ

vel a√yy+aa/y-aa/y=Iδ^12)

a√vv+aa/v-aa/v=Kζ si QD sit v.

Iδ:Kζ=IS:KT=a√yy+aa/y-aa/y:a√vv+aa/v-aa/v.

ratio IS ad KT √yy+aa/y-a/y:√vv+aa/v-a/v

composita { √yy+aa-a	:	√vv+aa-a
composita {      v	:	y

√yy+aa-a(Eθ)¹³⁾:y(EB)=√vv+aa-á(Egl):y√vv+aa-ya/√yy+aa-a (Eπ)

EN:Eπ=v:y√vv+aa-ya/√yy+aa-a

Est enim haec ratio eadem ac composita praecedens. Ergo ▭ φC in a est==spat. HQDβ et φC=q.

[curva] AB=XB-XN (sive λθ)+φC

Eadem igitur constructio hic oritur quae ex Hospitalij investigatione pag. 150¹⁴⁾.

EF est subtangens. Fθ=FB. Fλ=FN. λπ parall. θB.

10) Huygens applique ici, sous une autre forme, la propriété 15 de la logarithmique, que l'on rencontre p. 179 de l'édition originale du ‘Discours de la cause de la pesanteur’.

11) Dès ce moment il ne s'agit plus que de construire une ligne Eπ de telle manière qu'on ait EN:Eπ=IS:TK, puisque alors a × φC=spat. IIQDβ=α × q, donc q=φC; mais, comme nous l'avons expliqué dans la note 7 de la Lettre N^o. 2777, il est probable que Huygens connaissait déjà la construction de cette ligne φC, telle qu'on la rencontre dans le texte de la Lettre N^o. 2777, obtenue par lui comme une simplification de celle de de l'Hospital. Il n'avait donc plus qu'à vérifier si le rapport EN:Eπ, tel qu'il résultait de cette construction, était le même que celui de IS à KT. C'est ce qu'on verra accompli dans ce qui va suivre.

12) Ici les expressions en x sont remplacées par celles en y en vertu de l'équation x²y²=a²y²+a⁴ de la courbe VHQ.

13) Puisque, d'après la construction mentionnée, Fθ=FB=√a²+y², Fλ=FN.

14) C'est-à-dire telle que Huygens l'avait simplifiée, simplification que l'on rencontre en effet à la page citée, où elle est précédée du titre: ‘Brevissima constructio problematis Hospitalij’. Il serait inutile de la reproduire ici, parce qu'elle est identique avec la construction indiquée par Huygens, dans la Lettre N^o. 2777 et dans l'article mentionné dans la note 1 de cette pièce.