Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 356]

N^o 2778.
Christiaan Huygens.
[septembre ou octobre 1692].
Appendice I¹⁾ au No. 2777.

La pièce se trouve à Leiden, coll. Huygens.

BF hyperbole aequilatera; centro A, axe ABC. FE tangens. KAE perp. BA. FK perp. EAK. KD est ▭; erit punctum D ad curvam DL²⁾, cujus asymptoti BC, BM parall. AE. Et sptatium infinitum LDFBM aequale spatio FBAK.

Nam ut FD ad DE sive FK, ita PO ad OF; unde ▭ FK, PO==▭ FD, FO.

y³⁾ (FK=CA=DE):a(BA)

=a(BA):aa/y(HA)

CB=y-a

y-a

2a/y+a

AK=CF=y-a/√yy-aa

AE=x

EK=x+√yy-aa

x(EA):aa/y(AH)=x+√yy-aa(EK):y(FK)

xyy=aax+aa√yy-aa

xyy-aax=aa√yy-aa

1) Cet appendice contient la réduction de la quadrature de la courbe x²y²-a²x²=a⁴ à celle de l'hyperbole. Il est emprunté à la page 108 du livre H.

2) On doit considérer ce qui précède comme la définition de la courbe LD.

3) Ici commence la déduction de l'équation de la courbe LD.

[p. 357]

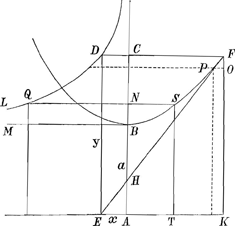
per yy-aa xxy⁴-2xxaayy+a⁴xx=a⁴yy-a⁶/xxyy-aaxx=a⁴, aequatio curvae DL, quae quadrabilis ex quadratura hyperbolae.

Etiam portionis cujusvis CDQN mensura dabitur ex quadratura spatii hyperbolici FSTK; huic enim aequale est spatium FDQSF; datur autem et spatium FSNC ex dato FSTK. Ergo et CDQN quod nempe aequale erit FSTK-FCNS.

Haec [QD] est curva qua Jo. Bernoulius utitur in constructione Catenariae in fig. 1⁴⁾. Et ex qua etiam alteram invenit optimam quae fig. 2^da. Itaque scivit hujus quadraturam pendere ex quadratura hyperbolae⁵⁾. Sed nondum video quomodo ad hanc curvam devenerit in illo problemate⁶⁾.

4) En effet, il est facile de vérifier que la courbe, employée à cette construction par Jean Bernoulli dans l'article cité dans la note 12 de la Lettre N^o. 2664, possède cette même équation x²y²-a²x²=a⁴.

5) Puisque Bernoulli faisait dépendre cette seconde construction de la rectification de la parabole, qu'on savait dépendre à son tour de la quadrature de l'hyperbole; tandis que la première construction dépendait de celle de la courbe mentionnée.

6) On peut retrouver la voie suivie par Bernoulli, laquelle intrigua si vivement Christiaan Huygens (comparez encore la Lettre N^o. 2695), dans l'ouvrage cité dans la note 30 de la Lettre N^o. 2693, où la même courbe est employée dans la construction de la chaînette. (Voir les ‘Lectiones’ 36 et 12).