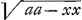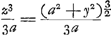Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2664.
| |
[pagina 50]
| |
par la diminution de la vistesse du corps, qui la sent, et je m'estois assés expliqué la dessus dans tout mon discours, mais j'advouë qu'il demande de l'attention. Je ne scay si vous aurés examiné ce que je dis de la resistence absolueGa naar voetnoot4), comme il s'en trouve dans le frottement. Il est tres vray, comme vous avés remarqué, Monsieur, que dans un jet libre par un milieu resistent, la simple composition des deux mouvemens ne peut avoir lieu et pour que mon article 6. puisse trouver place, il faut une hypothese particuliereGa naar voetnoot5). Ce peu que j'ay vû de Mr. Fatio me le fait estimer, et j'attends beaucoup de sa penetration. Je suis bien aise d'entendre qu'il est à la Haye, et je luy envierois ce bonheur, dont il ne m'est pas permis de jouir, si je ne considerois, qu'il profitera beaucoup en vous voyant quelques fois, et qu'il en sera d'autant plus en estat de rendre service au public. Il n'a pas mal choisi en se mettant à chercher les courbes dont les tangentes sont d'une nature connue, c'est presque ce qu'il y a de plus difficile et de plus important en Geometrie; je contribuerois volontiers à l'aider si je puis dans cette recherche, s'il en croyoit avoir besoin. Comme il a aussi trouvé vos courbes je m'imagine qu'il aura pris quelque biais, qui serve à abreger; comme en effect je puis fabriquer plusieurs canons particuliers pour retrancher le calcul. Pour ce qui est d'une courbe dont la soutangente soit yy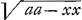 : ax j'ay trouvé qu'il y en a plusieurs, qui y peuvent satisfaireGa naar voetnoot6), mais les plus simples sont comme je croy celles dont les equations
sont aaxx=a4-y4, ou bien 4aaxx=4aayy-y4. Le calcul fera connoistre que tant l'une que l'autre reussit. Si M. Fatio trouve bon de me communiquer sa methode pour vos deux lignes, je luy communiqueray la mienne pour ces deux d'à present, où il a trouvé de la difficulté. J'avois crû que l'aire de la courbe dont l'equation est 2aaxx=aayy+y4 dependoit de la quadrature de l'hyperbole, mais ayant revû mon calcul, je trouve qu'elle est quadrable : ax j'ay trouvé qu'il y en a plusieurs, qui y peuvent satisfaireGa naar voetnoot6), mais les plus simples sont comme je croy celles dont les equations
sont aaxx=a4-y4, ou bien 4aaxx=4aayy-y4. Le calcul fera connoistre que tant l'une que l'autre reussit. Si M. Fatio trouve bon de me communiquer sa methode pour vos deux lignes, je luy communiqueray la mienne pour ces deux d'à present, où il a trouvé de la difficulté. J'avois crû que l'aire de la courbe dont l'equation est 2aaxx=aayy+y4 dependoit de la quadrature de l'hyperbole, mais ayant revû mon calcul, je trouve qu'elle est quadrable
| |
[pagina 51]
| |
absolument aussi bien que l'autre, dont l'equation est 2aaxx=aayy-y4Ga naar voetnoot7). Et comme vous me demandés la determination de l'aire de la derniere, asin que M.
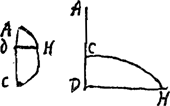 Fatio se puisse asseurer que je l'ay trouvée, de quoy il avoit douté, parce qu'il n'y avoit pas reussi luy même, je vous donneray les aires des parties quelconques de toutes deux. Soit AC, a et AD, y, et DH, x, et aaxx=aayy-y4, et soit 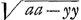 = z, je dis que ADHA est = z, je dis que ADHA est 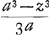 et par consequent ACHA estant a3/3a, CDHC sera z3/3aGa naar voetnoot8). Caeteris iisdem positis, soit aaxx=aayy+y4 et soit et par consequent ACHA estant a3/3a, CDHC sera z3/3aGa naar voetnoot8). Caeteris iisdem positis, soit aaxx=aayy+y4 et soit 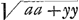 = z, je dis que CDHC est z3/3aGa naar voetnoot9), comme auparavant si au lieu de aaxx on met 2aaxx comme vous le demandés, on n'a qu'à écrire 3a√2 au lieu de
3a. = z, je dis que CDHC est z3/3aGa naar voetnoot9), comme auparavant si au lieu de aaxx on met 2aaxx comme vous le demandés, on n'a qu'à écrire 3a√2 au lieu de
3a.
Puisque la premiere achevée retourne en elle meme, en forme de 8Ga naar voetnoot10), on en peut juger que le theoreme de Mr. NewtonGa naar voetnoot11) p. 105, qui pretend, qu'il n'y a point de courbe recourrante (de la Geometrie ordinaire) indefiniment quadrable, ne scauroit subsister, et qu'il y a quelque faute dans sa demonstration. Mais je ne l'en estime pas moins; Opere in longo fas est obrepere somnum. M. Bernoulli a aussi trouvé ensin la ligne de la chaineGa naar voetnoot12). Je croy que la connoissance de mon calcul l'aura un peu aidé, car quoy que ce probleme ne soit pas des plus difficiles, je m'imagine qu'il n'est pas trop aisé d'y reussir sans avoir quelque chose d'equivalent à ce calcul. Je n'ay pas vû sa solution, je ne laisse pas de croire qu'il a donné dans le but. Mons. Tschirnhaus n'y a pas mordu, quoique j'aye parlé expres d'une maniere à l'y engagerGa naar voetnoot13), pour luy donner occasion d'exercer sa methode, dont il nous pro- | |
[pagina 52]
| |
mettoit tant, jusqu'à me reprendre obliquement, de ce que j'avois dit que l'Analyse ordinaire ne suffit pas dans ces rencontres. Je croy que Mr. Fatio est allé trop viste en pretendant que mon Exponentiale est impossible. Je verray un de ces jours, si je vous en pourray donner la construction. On ne donnera la solution de M. Bernoulli que quand j'auray envoyé la mienne; et si vous le trouvés à propos nous y joindrons la vostre, mais j'espere de la voir prealablement, et de vous faire juger de la mienne. Ga naar voetnoot14) Je voudrois bien scavoir ce que vous jugés des variations de l'eguille aimantée et des causes de l'inclination. Et s'il est bien seur, que dans des lieux qui ne sont pas eloignés l'un de l'autre il se trouue une grande difference entre les declinaisons. Je suis disposé à croire que cela n'est point. Mais l'experience en doit juger souuerainement. Je desire aussi de scavoir vostre sentiment sur la cause du flus et reflus de Mr. Des CartesGa naar voetnoot15). Je me souuiens que vous avés traité autres fois de la cause des parelies. J'espere que vous en mettrés la demonstration dans vostre dioptrique, et que vous nous donnerés apres tant de delais cet ouvrage si desiré. M. Newton n'a pas traité des loix du ressort; il me semble de vous avoir entendu dire autres fois que vous les aviés examinées, et que vous aviés demonstré l'isochronisme des vibrations. N'y a-t-il personne à present qui medite en philosophe sur la medecine? Feu Mr. CraneGa naar voetnoot16) y estoit propre, mais Messieurs les Cartesiens sont trop prevenus de leur hypotheses. J'aime mieux un Leeuwenhoek qui me dit ce qu'il voit, qu'un Cartesien qui me dit ce qu'il pense. Il est pourtant necessaire de joindre le raisonnement aux observations. Mais je finis en me qualifiant avec beaucoup de zele
Monsieur
Vostre treshumble et tresobeissant seruiteur Leibniz. |
|