Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2643.
Christiaan Huygens à G.W. Leibniz.
19 décembre 1690.

La lettre se trouve a Hanover, Bibliothèque royale.
La minute se trouve à Leiden, coll. Huygens¹⁾.
La lettre a été publiée par P.J. Uylenbroek²⁾ et C.I. Gerhardt³⁾.
Elle est la réponse aux Nos. 2636 et 2639.
Leibniz y répondit par la lettre du 6 février 1691.

A la Haye ce 19 Decembre 1690.

Monsieur

A cause d'un voiage de quelques jours, que j'ay estè obligè de faire à Amsterdam⁴⁾, pour avoir soin de l'embarquement de mes Pendules dans les vaisseaux qui vont aux Indes, je n'ay pu repondre plus tost à deux lettres que j'ay eu l'honneur de recevoir de vostre part.

J'estime beaucoup vostre solution pour ma seconde ligne courbe, et si vous avez une methode qui reussisse tousjours, quand ce ne seroit que lorsque la courbe est

1) Un brouillon de cette lettre se trouve aux pages 73 recto et verso du livre G des Adversaria. Il diffère assez notablement de la lettre même, surtout dans l'ordre des sujets traités. Toutefois le brouillon ne contient presque rien qui ne se retrouve sous une forme ou autre dans la lettre envoyée. Nous nous bornerons donc à marquer dans les notes les endroits où la différence des deux pièces est la plus sensible. La minute, écrite sur une feuille isolée, ne diffère pas sensiblement du texte donné par Gerhardt, d'après le manuscrit de Hannover.

2) Chr. Hugenii Exercitationes Mathematicae, etc. Fasc. I, p. 55.

3) Leibnizens Mathematische Schriften, Bd. II, p. 68 et Briefwechsel von G.W. Leibniz, p. 625.

4) Voir les Lettres N^os. 2638 et 2642.

[p. 569]

ordinaire, vous augmenterez la Geometrie d'une invention fort considerable en la donnant au public. Mais j'ay tousjours de la peine à croire que la regle universelle se puisse trouver, sur tout quand les termes algebraiques de la construction donnée pour la Tangente sont beaucoup deguisez par la substitution des valeurs⁵⁾. Et il faudroit encore une preuve, où il y eust plus de difficultè que dans ma dite courbe. Mais je ne veux pas vous en donner la peine, si vous ne le souhaitez vous mesme. Il me semble que dans cette courbe, par un calcul retrograde⁶⁾ on peut connoistre l'equation d'où les termes de la construction ont estè produits: et sur tout cela n'est pas difficile dans ce cas, où vous avez trouvè l'équation de 6 dimensions, scavoir où la soutangente estoit donnée yy/2x - 2x. Je me sers icy de vostre correction pour les signes + et -⁷⁾, et j'avoue que dans toutes les deux courbes je les devois avoir mis comme vous dites, parce qu'en suivant simplement l'operation de la Regle⁸⁾, les termes viennent de cette façon. Mais comme j'ay accoutumè de m'en servir avec des signes contraires au numerateur, en avertissant de quel costè la tangente doit estre prise, cela a estè cause de ce renversement. J'ay autrefois ecrit la demonstration et origine de cette Regle des Tangentes, et Mrs. de l'Academie de Paris ont fait imprimer ce petit traité⁹⁾ depuis peu avec quelques autres, tant de moy que de quelques uns d'entre eux. Il y a là aussi de moy une nouvelle demonstration pour l'équilibre de la Balance, la quelle je seray bien aise que vous voyez; celle d'Archimede m'ayant tousjours paru defectueuse, ainsi qu'à bien d'autres; mais on ne peut rien avoir de ce qu'on imprime en France.

Pour ce qui est de vostre courbe de quatre dimensions, dont l'equation est 2r⁴xx ∞ r⁴ yy+aay⁴, ou ce qui est la mesme chose, 2aaxx = aayy + y⁴, elle satisfait parfaitement, je l'avouë, à ma soutangente donnée - yy/2x + 2x. Et pourtant ce n'est pas là l'equation de ma courbe dont j'avois tirè ces termes, ce qui peutestre vous surprendra¹⁰⁾. Mon equation estoit 2aaxx = aayy - y⁴, qui donne tout une autre courbe que la vostre¹¹⁾. Il sembleroit d'abord qu'il y auroit une mesme construction de tangente pour deux courbes differentes, mais a y prendre

5) Consultez, sur ces déguisements, la note 10 de la lettre N^o. 2611, et l'Appendice N^o. 2612.

6) Voir, sur ce calcul rétrograde, l'Appendice N^o. 2644 de cette lettre, aux §§ I et II.

7) Voir la pièce N^o. 2612, note 3.

8) Il s'agit de la règle, telle qu'elle avait été formulée p.e. par de Sluse dans l'article cité dans la Lettre N^o. 1924, note 1.

9) Voir la Lettre N^o. 2435, note 1.

10) Le brouillon ajoute en marge: ‘il y a là matiere pour une profonde speculation’. Voir la Lettre N^o. 2639, note 3.

11) Voir, sur ces deux courbes et leurs équations, les §§. III et IV de l'Appendice à cette lettre.

[p. 570]

bien garde, on voit que les constructions different aussi, par ce que dans la vostre la quantité - yy + 4xx est tousjours affirmative, et que dans la miene elle est tousjours negative¹²⁾. Vostre ligne a la figure d'une croix ainsi et la miene celle de deux demi-ovales posées à certaine distance



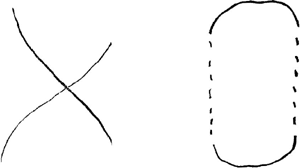Celle-cy se peut quadrer¹³⁾, ce que je ne scay s'il convient aussi à la vostre. Je voudrois bien essaier dans toutes deux ce que pourroit faire Mr. D.T. par la methode qu'il pretend d'avoir¹⁴⁾.

Touchant la courde exponentiale que vous avez trouvée pour ma premiere soutangente donnée 2xxy - aax / 3aa - 2xy, je vous prie de me dire si vous pouvez representer la forme de cette courbe en y marquant des points ou par quelque maniere que ce soit, ou si cela vous sert seulement à pouvoir decider qu'il n'y a point de courbe ordinaire qui y convienne, ni de transcendante non exponentiale, comme sont les cycloides, quadratrices, etc.

J'ay dit que vostre equation 2r⁴xx ∞ r⁴yy + aay⁴ ne differe pas de 2aaxx ∞ aayy + y⁴. Et cela paroit parce qu'elle se reduit à 2r⁴xx/aa ∞ r⁴yy/aa + y⁴, et que r⁴/aa est une quantité donnée. Par consequent cette courbe ne se peut point varier, comme vous avez creu, en changeant la proportion de a à r; non plus que la la parabole se varie en prenant le parametre plus ou moins grand. Par la mesme

12) Voir, sur la portée de cette remarque et sur les particularités de ces figures, la note 10 de l'Appendice N^o. 2644 à cette lettre.

13) Cette quadrature à été reproduite dans l'Appendice N^o. 2612, de la lettre N^o. 2611. Elle repose sur la réduction de l'équation y⁴ - 8 aayy + 16 aaxx = 0 à la forme:
y = √2aa + 2ax + √2aa - 2ax = y′ + y″, où y′=√2aa + 2ax et y″ = = √2aa - 2ax représentent les paraboles AF et BG de la figure de l'Appendice cité.

14) Allusion à l'article cité dans la Lettre N^o. 2324, note 19. Consultez encore la Lettre N^o. 2627, note 11.

[p. 571]

raison vostre equation de 6 dimensions 6a⁶xxy⁴ ∞ a⁶y⁶ + r¹² revient à 6xxy⁴ ∞ y⁶ + a⁶, et la courbe est de mesme invariable.

Il y a plus d'un an que j'ay receu 2 lettres de M. Fatio¹⁵⁾, dans les quelles il propose une Regle renversée des Tangentes, mais comme elle paroissoit d'une longue discussion, et que d'ailleurs je ne pouvois croire qu'elle fust parfaite¹⁶⁾, j'ay estè jusqu'icy sans l'examiner: ce que j'ay maintenant envie de faire, mais je n'ay pas ces lettres dans cette ville.

Je ne scay pas pourquoy vous voulez que j'aye prononcè trop severement contre les courbes exponentiales, puis que je n'ay pretendu les rejetter qu'en cas qu'elles ne soient de nulle utilité. Car si elles vous servent d'exprimer d'autres courbes dont on a besoin, et si par leur moien vous trouvez les espaces des chutes par un medium resistens lors que les temps sont donnez, et que de plus elles vous aident à trouver les courbes par la proprietè des tangentes, je les estimeray grandement, car je n'aime rien tant que les nouveautez qui tendent à l'accroissement des sciences. Il s'agit de scavoir s'il est bien seur qu'on en peut tirer tous ces avantages; ce que voulant me prouver vous supposez que j'entens parfaitement tout vostre calcul des equations Exponentiales et Logarithmiques, ce qui n'est point; et ainsi vous instruisez le proces (pour demeurer dans les termes de vostre similitude) devant un juge qui n'entend pas bien vostre langue. Je n'ose pas aussi vous demander plus d'eclaircissement, voiant bien que cela seroit trop long pour des lettres. Je souhaiterois de vous pouvoir entretenir coram sur ces matieres, et je ne desespere pas qu'à cette occasion, que les Princes d'Allemagne vont venir icy à l'arrivée du Roy d'Angleterre, Mr. le Duc de Hanovre ne s'y rende aussi, et vous, Monsieur, à la suite de Son Altesse, dont certainement j'aurois bien de la joye.

Les Acta de Leipsich ne nous vienent icy que de deux en deux mois; ainsi je n'ay pas encore vu ceux de Novembre, où vous dites qu'on a fait une bevue à l'egard de ma progression pour la quadrature de l'Hyperbole¹⁷⁾. Cependant comme cela me fait tort, vous m'obligerez si vous pouvez faire en sorte qu'il soit redressè. Vostre excuse au reste est merveilleuse, quand vous m'assurez de n'avoir aucune part à ce mesentendu. J'adjoute icy à propos de cette quadrature que je ne vois pas que vostre progression¹⁸⁾ v + ⅓v³ + ⅕v⁵ &c. responde à la

15) Nous ne connaissons d'autre lettre de Fatio sur la ‘règle renversée des tangentes’ que la Lettre N^o. 2465 du 24 juin 1687. La seconde était probablement celle dont il est question dans la Lettre N^o. 2523, note 2.

16) Consultez la note 12 de la Lettre N^o. 2465 et la lettre de Huygens à de l'Hospital du 23 juillet 1693.

17) Voir les notes 12 et 13 de la Lettre N^o. 2636.

18) Il s'agit de la quadrature de l'aire BG + BE dont il est question dans la Lettre N^o. 2639.

[p. 572]

mienne¹⁹⁾, parce que vous ne vous servez pas, comme moy, de la tangente du secteur hyperbolique pour en faire v lors que le demi axe est 1. L'application que vous en faites aux chutes des corps est encore bien obscure, et vous devez l'avouer vous mesme, apres les corrections reiterées que vous avez apportées à ce raisonnement. Et quant aux resistences de l'air, s'il est vray que vous les ayez considerées comme estant en proportion double des vitesses il faut au moins changer l'inscription de l'article 5²⁰⁾ de vostre derniere mettant proportione quadratorum velocitatis.

J'ay le livre de Mr. Guericke où il raporte ses experiences de l'ambre. S'il vous en a communiquè encore d'autres, je seray bien aise d'y participer. Plusieurs des miennes²¹⁾ ont estè faites en vue de certaines hypotheses, que je me suis imaginées pour expliquer cette admirable attraction et ses divers phenomenes, mais je ne suis pas encor venu à bout de cette speculation. Je vous demande pardon de vous avoir derobè du temps par une si longue lettre et de croire que je suis²²⁾ etc.

19) Celle du ‘Discours de la pesanteur’ dont nous avons traité dans les notes 7 et 13 de la lettre N^o. 2632 et qui en effet se rapporte à une autre partie de l'hyperbole. Voici d'ailleurs la



leçon du passage qui va suivre, telle qu'elle se trouve dans le brouillon: ‘Ce qu'il apporte pour montrer que par son équation exponentiale il peut trouver les espaces des chutes quand les temps sont donnez, et comment la progression de v + ⅓v² + ⅕v⁵ etc. provient de son calcul, est tres obscur. Je n'y vois cependant pas que vous vous serviez de la tangente AF du secteur hyperbolique ACB (je mets icy la figure qui est dans mon livre pag. 175) pour en faire v dans la progression lors que AD est l'unité.’

20) Voir sur cet article qui porte l'inscription: ‘Si motus a gravitate acceleratus a medio uniformi retardetur proportione velocitatis’, la note 9 de la Lettre N^o. 2632.

21) Dans les livres des Adversaria de Huygens on ne trouve que de rares traces d'expériences électriques. La plus ancienne, datée du 27 avril 1672, est la description du procédé de fabriquer des boules de soufre. Un allemand, dont Huygens ne cite pas le nom, mais ‘qui l'avait appris de M. Otto Gericke’ lui montra la manière de fondre du soufre concassé dans un matras de verre, que l'on brisait après refroidissement pour en retirer la boule.

22) Le brouillon contient encore la phrase suivante, qui ne se retrouve pas dans la lettre: ‘comment avoir la somme de quelque progression harmonique comme ⅕ + 1/9 + 1/13 + 1/17 etc., qu'il dit se pouvoir trouver compendio aliquo’. Cette phrase fait allusion au passage suivant, que l'on rencontre dans l'article de Leibniz dans les Acta de février 1682, cité dans la note 13 de la Lettre N^o. 2636.
‘Itaque cum Circulus sit 1/1 + ⅕ + 1/9 + 1/13 + 1/17 etc. - ⅓ - 1/7 - 1/11 - 1/15 - 1/19 etc., posteriorem seriem partialem, a priori subtrahendo, erit magnitudo Circuli, differentia duarum serierum progressionis harmonicae. Et quoniam quotcunque terminorum numero finitorum progressionis harmonicae summa, compendio aliquo inveniri potest, hinc appropinquationes compendiosae, (si post Ludolphinam illis esset opus) duci possent.’