|
| |
| |
| |
No 2632.
G.W. Leibniz à Christiaan Huygens.
[novembre] 1690.
La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. UylenbrockGa naar voetnoot1) et par C.J. GerhardtGa naar voetnoot2).
La lettre sait suite au No. 2627.
Chr. Huygens y répondit par le No. 2633.
Monsieur
Vous aures receu la lettre que je me suis donné l'honneur de vous écrire, et ou je reponds touchant les lignes que vous me proposés à chercher par ma methode; et touchant la Ligne de la corde pendante. Je n'ay pas encore mis au net une lettre plus longueGa naar voetnoot3), ou je mets mes pensées sur le mouuement des planetes. Cependant vous l'aurés aussitost que je pourray m'y attacher assez pour cet effect, et j'en espere alors vostre jugement. Cependant je crois que par ce peu que j'auois dit de la chaine pendante, vous jugerés si je me suis rencontré avec vous sans qu'il faille d'autre chiffre, et j'en espere des nouuelles quand vostre commodité le permettra.
Il m'est venu dans l'esprit cependant, que l'equation que j'auois donnée pour vostre courbe, pourroit embarasser, n'estant pas aisé de juger, si elle peut satisfaire à vostre demande, puisqu'on n'a pas encor donné moyen de trouuer les tangentes par des equations où l'exposant est inconnu. Et quoyque je n'aye pas encor communiqué à d'autres la methode dont je me sers pour cet effect, je ne laisse pas de vous en envoyer icy un echantillon par le quel vous la connoistrés assés.
Soit donc x l'abscisse et y l'ordonnée de la courbe, et l'equation, comme je vous ay dit, x3y/h = b2xy/.. Je designeray le logarithme de x par log. x, et nous aurons 3 log. x + log. y - log. h = 2 x y, supposant que le log. de l'unité soit o, et le log. b = 1. Donc par la quadrature de l'hyperbole nous aurons 3 ∫ dx/x + ∫ dy/y - log. h=2xy, dont l'equation differentielle sera 3dx/x + dy/y = 2xdy + 2ydx, ou bien 3ydx + xdy = 2xx ydy + 2xyydx, et par consequent dx sera à dy, ou bien DB à y (selon la figure de la lettre precedente) comme 2xxy - x est à 3y - 2xyy, c'est a dire DB sera 2xxy - xaa/3aa - 2xy comme vous le demandiés, a estant l'unité.
| |
| |
Je croy, Monsieur, que vous trouverés ce calcul nouveau, et de consequence. L'analyse Transcendente seroit portée à sa perfection si on la pouuoit tousjours reduire à de telles equations. Les equations differentielles sont un acheminement pour cet effect. J'ay beaucoup medité sur ce qu'il y a à faire la dessus, et si j'auois le loisir necessaire, ou si quelque jeune mathematicien intelligent estoit proche de moy pour m'assister, je croy qu'on pourroit avancer cette science bien au de là de l'estat où elle se trouve. Plût à Dieu, qu'on pût avancer en physique à proportion.
Que jugés vous, Monsieur, de l'explication du flus et reflus de Mons. NewtonGa naar voetnoot4)? et vous paroist il raisonnable, que les queues des cometes soyent une matiere effective, poussée hors de la comete à des distances immenses, et qui ne laisse pas de suivre son mouuementGa naar voetnoot5)? Je les aurois plus tost pris pour un effect optique.
Un Écossois qui estoit en Hollande, nommé Mr. StearGa naar voetnoot6) dit dans sa physiologie d'auoir experimenté que les corps poussés dans le vuide d'air ne vont pas fort loin; j'ay de la peine à le croire. N'a-t-on rien decouuert sur les loix de la variation de l'eguille aimantée? Je m'imagine, Monsieur, que vous aurés medité la dessus, aussi bien que sur beaucoup d'autres matieres de physique, et je vous supplie de me faire quelques fois part de vos lumieres, quand même ce ne seroient que des conjectures, puisque vos conjectures mêmes valent mieux que les demonstrations de bien des gens. C'est à cet effect que je vous ay demandé vos sentimens dans cette lettre, aussi bien que dans la precedente, sur certains points, et j'espere que vous me connoissés assez, pour ne vous pas defier de ma sincérité.
ConsiderantGa naar voetnoot7) ce que j'ay dit de la resistance du milieu dans les Actes de Leipzig,
| |
| |
Fevrier 1689Ga naar voetnoot8), vous trouverés, Monsieur, article 5. n. 3Ga naar voetnoot9) qu'encor chez moy (les elemens des temps estant pris egaux, condition que vous et Mr. Newton avés dissimulée) les resistences sont comme les quarrés des vistesses, et par le nombre 4 et 6 de cet articleGa naar voetnoot10), il s'ensuit aussi que la somme a + ⅓ a3 + ⅕ a5 etc., se reduit a la quadrature de l'hyperboleGa naar voetnoot11). Dans l'ouurage que j'avois composé autres fois sur la quadrature ArithmetiqueGa naar voetnoot12), je trouue cette proposition generale: Sector comprehensus arcu sectionis Conicae a vertice incipiente et rectis ex centro ad ejus extrema ductis, aequatur rectangulo sub semilatere transverso et recta t ± ⅓ t3 + ⅕ t5 ± 1/7 t7 etc. posito t esse portionem tangentis in vertice, inter verticem et tangentemGa naar einda) alterius extremi interceptam, et rectangulum sub dimidiis lateribus recto et transverso (id est quadratum a semiaxe transverso) esse unitatem. Est autem ± in hyperbola + in Ellipse vel circulo -.
| |
| |
Quelqu'un m'a dit qu'on scait en Hollande la carte de l'Asie Septentrionale, et si l'Amerique en est divisée par la mer. Si vous en scavés quelque chose, je vous supplie de m'en dire un mot. Voila à quoy votre bonté et vostre scauoir vous exposent. Mais il est tousjours bon d'estre riche au hazard d'estre importuné par des pauvres. Je suis avec zele
Monsieur
Vostre treshumble et tresobeissant seruiteur Leibniz. |
-
voetnoot1)
- Chr. Hugenii Exercitationes Mathematicae etc. Fasc. I, p. 36.
-
voetnoot2)
- Leibnizens Mathematische Schriften, Bd. II, p. 53, et Briefwechsel, p. 604.
-
voetnoot3)
- Il s'agit de la pièce No. 2628, qui n'a jamais été envoyée à Huygens.
-
voetnoot4)
- Voir les prop. XXIV, XXXVI et XXXVII du Livre III des Principia.
-
voetnoot5)
- Voir la prop. XLI du livre III des Principia.
-
voetnoot6)
- Il s'agit de D. de Stair et de son ouvrage:
Physiologia nova Experimentalis Auctore D. de Stair, Carolo II Britanniarum Regi a Consiliis Juris & Status, nuper Latinitate donata. Lugduni Batavorum apud Cornelium Boutesteyn, 1686, in-4o.
-
voetnoot7)
- Pour faciliter l'intelligence de ce qui va suivre nous croyons utile de citer ici les passages suivants, qui se trouvent aux pages 173, 174 et 175 du Discours sur la cause de la pesanteur et auxquels les remarques de Leibniz se rapportent:
‘En examinant ce qui arrive dans la vraye hypothese de la Resistance, qui est en raison double de la Vitesse, j'avois seulement determiné ce cas particulier d'un corps jetté en haut avec sa vitesse Terminale’...‘Je n'avois point recherché les autres cas, qui sont compris universellement dans la prop. 9, du 2 Livre de Mr. Newton, qui est tres belle: & ce qui m'en empêcha, ce fut que je ne trouvois point, par la voie que je suivois, la mesure des descentes des corps, si non en supposant la quadrature de certaine Ligne courbe, que je ne sçavois pas qu'elle dependoit de la quadrature de l'Hyperbole. Je reduisis la dimension de l'espace de cette courbe, à une Progression in finie, a + ⅓ a3 + ⅕ a5 + 1/7 a7 &c. Ne sçachant pas que la mesme proportion donnoit aussi la mesure du secteur Hyperbolique: ce que j'ay vu depuis, en comparant la demonstration de Mr. Newton avec ce que j'avais trouvé. Mais par ce que cette Progression pour la mesure de l'Hyperbole, n'a pas encore esté remarquée que je scache, je veux expliquer icy comment elle y sert’....‘De sorte que cette Progression pour l'Hyperbole, respond à celle qu'a donné Mr. Leibnits pour le Cercle.’
-
voetnoot8)
- Lisez: Janvier. Il s'agit de l'article cité dans la Lettre No. 2561, note 6.
-
voetnoot9)
- Allusion à la phrase suivante: ‘Nam ex prop. 1 (hic) sequitur resistentias esse in composita ratione elementorum temporis et quadratorum velocitatum’. De cette phrase on pouvait inférer en effet que dans l'Article 5 il s'agit du cas d'une résistance proportionelle au carré de la vitesse; mais la suscription de l'article lui-même: ‘Si motus a gravitate acceleratus a medio uniformi retardetur proportione velocitatis’ était bien propre à induire en erreur. Dans la suite de la correspondance on verra d'ailleurs les raisons pour lesquelles Leibniz avait donné à l'article ce titre singulier.
-
voetnoot10)
- Ces numéros contiennent la solution de Leibniz du problème de la chute d'un corps grave sous l'influence d'une résistance proportionelle au carré de la vitesse. Comme ils reviendront plusieurs fois dans la correspondance qui va suivre, nous croyons utile de reproduire ici les résultats énoncés dans la forme que Leibniz leur a donnée, accompagnés d'une traduction algébrique que nous y avons ajoutée. Les voici:
4. ‘Si rationes inter summam et differentiam velocitatis maximae et minoris assumtae, sunt ut numeri; tempor a quibus assumtae velocitates sunt acquisitae, erunt ut Logarithmi’
(t:t' = l a + v / a - v:l a + v' / a - v' où a représente la vitesse terminale et où les temps sont comptés depuis le commencement de la chute).
6. ‘Si velocitates acquisitae sunt ut sinus, erunt spatia percursa ut Logarithmi sinuum complimenti posito radium seu sinum totum esse ut velocitatem maximam.’
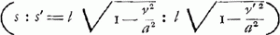
-
voetnoot11)
- Comme on sait, la réduction aux logarithmes implique celle à la quadrature de l'hyperbole et comme Huygens avait réduit le problème à la sommation de la série citée et Leibniz aux logarithmes, il s'ensuivit que cette sommation elle-même était réduisible à la quadrature de l'hyperbole.
-
einda)
- Secantem [Christiaan Huygens]Ga naar voetnoot13).
-
voetnoot13)
- Cette correction a pour but de rapprocher le théorème énoncé ici par Leibniz à la quadrature de l'hyperbole, telle qu'elle avait été trouvée par Huygens et décrite aux pages 174 et 175 du ‘Discours de la pesanteur’; mais elle repose sur un malentendu. En effet, ces deux quadratures, celle de Huygens et celle de Leibniz telle qu'elle est formulée ici, sont exactes toutes les deux, mais différentes, quoiqu'elles dépendent de la sommation
de la même série. Pour le montrer nous allons les déduire au moyen des méthodes modernes.
Posant dans la figure ci-jointe, qui représente une hyperbole ABE avec son asymptote CD, CA = a, CH = b, CB = r, ∠ BCA = ϕ, nous partons de l'équation polaire:
r2 = a2 sec2 ϕ / 1 - a2/b2tg2 ϕ.
Elle nous donne immédiatement pour l'aire du secteur hyperbolique CABFC:
, où tgϕ = AF/CA.
Dans le cas de l'hyperbole équilatère, le seul dont Huygens s'occupe, ce résultat s'identifie avec celui de la page 174 du ‘Discours de la pesanteur’.
Maintenant pour obtenir le résultat de Leibniz, posons AK = x, BK = y; donc y2 = 2b2/ax + b2/a2x2. Alors on trouve facilement AT = t = b2x/ay, d'où il suit successivement: x = 2at2/b2 - t2; CK = a + x = a(b2 + t2) / b2 - t2; BK = y = 2b2t / b2 - t2; tg ϕ = BK/CK = 2b2t / a(b2 + t2); sec2 ϕ dϕ = 2b2(b2 - t2) / a(b2 + t2)2dt; 1 - a2/b2tg2ϕ = (b2 - t2 / b2 +
t2)2.
On a done encore:
Secteur hyperbolique
.
Identifiant alors, comme Leibniz le fait, le ‘semi-axis traversus’ b avec l'unité, on retrouve le résultat énoncé par lui dans le texte de la lettre. Une démonstration de Leibniz de ce théorème a été publiée d'ailleurs par Gerhardt; voir le ‘Compendium quadraturae arithmeticae’ (Leibnizens mathematische Schriften, Band V) à la page 109.
|