Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2561.
Christiaan Huygens à G.W. Leibniz.
8 février 1690¹⁾.

Le sommaire se trouve à Leiden, coll. Huygens.
La lettre se trouve à Hannover, Bibliothèque Royale.
Le sommaire a été publié par P.J. Uylenbroek²⁾.
La lettre a été publiée par C.I. Gerhardt³⁾.
Elle est la réponse au No. 2512.
Leibniz y répondit par sa lettre du 13 octobre suivant.

A.M. Leibniz⁴⁾.

9 Fevrier 1690.

Sommaire:

J'envoic un exemplaire du Traité de la Lumiere etc. J'ay receu sa tres obligeante lettre à l'occasion de son probleme que j'avois resolu, a laquelle je n'ay point repondu pour avoir trop differé, comme cela arrive, et parce que je scavois que j'aurois cette occasion icy. Que ce qu'il a escrit des Orbes Elliptiques dans les Acta de Leipsich estant conçu devant qu'il avoit veu le livre de Newton, mais seulement l'Extrait. s'il n'a pas changè d'avis depuis l'avoir iû et s'il n'a pas rejettè les tourbillons de des Cartes? Qu'il y a beaucoup d'obscuritè dans ce que luy Leibniz propose. plus que chez Newton. qu'il faudroit estre plus clair. Qu'il verra ce que j'escris du mouvement des corps empeschez par l'air, et ce qu'en a escrit Newton. Que je demande son jugement.

Il est bien tard de vous dire maintenant (si toutefois je ne dois pas l'omettre) que je reçûs la tres obligeante lettre que vous m'escrivistes il y a quelques 8 ou 10 mois, à l'occasion de Vostre Probleme dont vous aviez trouvé ma solution dans les Nouvelles des Sçavans⁵⁾. Je ne sçaurois vous dire pourquoy je n'y ay pas fait de response, si ce n'est par ce que je l'avais differée, comme cela arrive parfois, et que dès lors je prevoiois cette occasion presente de vous devoir enuoier le livre que j'allois faire imprimer. La lenteur des ouvriers, et un voiage que je fis en Angleterre depuis que l'édition estoit commencée, ont fait qu'elle a trainé jusqu'icy. Le

1) Nous adoptons la date de la lettre, celle du sommaire étant du jour suivant.

2) Chr. Hugenii etc. Exercitationes Mathematicae Fasc. I, page 22.

3) Leibnizens Mathematische Schriften. II, p. 40, et Der Briefwechsel von Leibniz, etc p. 593.

4) La lettre accompagna l'envoi d'un exemplaire du ‘Traité de la Lumière’, confié à van der Heck, agent du duc de Hannover; elle ne fut reçue par Leibniz que vers la fin du mois de septembre. Consultez la Lettre du 24 août 1690, de Huygens à Leibniz, et celle du 13 octobre 1690, de Leibniz.

5) Voir la pièce N^o. 2489.

[p. 367]

voila ensin achevé ce gros volume, et qui vous demande quelques heures de vostre loisir pour estre lû, comme à un juge tres competent en ces matieres. Outre le Traité de la Lumiere vous y verrez un discours de la cause de la Pesanteur, et ce que j'y ay adjoutè touchant les corps qui traversent l'air ou quelqu'autre milieu qui leur fait resistence, de quoy vous avez traitè aussi⁶⁾, et Mr. Newton plus amplement que pas un de nous deux⁷⁾. Je vois que vous vous estes encore rencontrè avec luy en ce qui regarde la cause naturelle des chemins Elliptiques des Planetes⁸⁾ mais

6) Dans les Acta Eruditorum de janvier 1689, sous le titre:
‘Schediasma de resistentia Medii, et Motu projectorum gravium in medio resistente’.

7) Dans les quatre premières sections du livre II des ‘Principia’, intitulées:
De motu corporum quibus resistitur in ratione velocitatis; De motu corporum quibus resistitur in duplicata ratione velocitatum; De motu corporum quae resistuntur partim in ratione velocitatis, partim in ejusdem ratione duplicata; De corporum circulari motu in mediis resistentibus.

8) Il s'agit de l'article de Leibniz dans les ‘Acta Eruditorum’ de février 1689, intitulé: ‘Tentamen de motuum coelestium causis’. Dans cet article remarquable Leibniz considère le mouvement d'une planète perpendiculaire au rayon vecteur (le mouvement circulatoire) comme causé par la présence d'un tourbillon Cartésien dans lequel les vitesses sont réciproquement proportionelles au rayon vecteur (un tourbillon harmonique, comme il l'appelle).
Après avoir déduit de cette hypothèse la deuxième loi de Kepler, il procède à l'étude du mouvement relatif le long du rayon vecteur. Il en cherche l'explication dans la coopération d'une force centrifuge, agissant conformément aux lois données pour la première fois par Huygens, et d'une sorce attractive. Au moyen de raisonnements et de calculs, justes au sond, quoique entachés d'une erreur importante, mais qui ne touche pas aux principes, il



démontre que dans l'orbite elliptique d'une planète cette force doit être réciproquement proportionelle au carré du rayon vecteur.
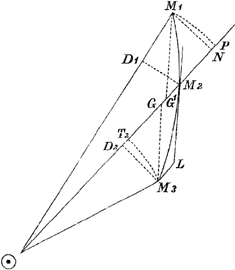
Ajoutons que l'erreur en question consiste en ceci, qu'il n'est pas permis de considérer les triangles M₁NM₂ et M₃D₂G de la figure ci-jointe, comme congruents, quoique en effet M₁N soit égal à M₃D₂ avec une approximation suffisante. On doit donc construire non seulement dans le secteur ☉M₃M₂ la droite M₃G parallèle à la tangente M₂L, comme Leibniz l'indique, mais de même, dans le secteur ☉M₁M₂, la droite M₁G'. Alors les raisonnements, appliqués par Leibniz, conduisent à la relation juste:
M₂P - T₂M₂ = 2 D₂T₂ - 2 M₃L, qui doit remplacer celle de Leibniz: M₂P - T₂M₂ = = 2D₂T₂ - M₃L.
Par suite de cette erreur, Leibniz trouve donc pour la force attractive le double de ce qu'elle est réellement, ce qui n'empêche pas qu'elle ne reste proportionelle au carré inverse du rayon vecteur.

[p. 368]

comme en traitant cette matiere vous n'aviez encore vû qu'un extrait de son livre⁹⁾ et non pas le livre mesme, je voudrois bien sçavoir si du depuis vous n'avez rien changé à vostre Theorie, parce que vous y faites entrer les Tourbillons de Mr. des Cartes, qui à mon avis¹⁰⁾ sont superflus, si on admet le Systeme de Mr. Newton où le mouvement des Planetes s'explique par la pesanteur vers le Soleil et la vis centrifuga, qui se contrebalancent. Outre que ces Tourbillons Cartesiens faisoient naitre plusieurs difficultés, comme vous verrez pas mes remarques et mesme sans elles vous ne pouviez pas l'ignorer. Je ne feray pas cette lettre plus longue, puisque je vous envoie assez d'ailleurs pour derober de vostre temps. Je vous supplieray seulement que lors que vous aurez examiné ces petits Traitez, de m'en faire sçavoir vostre sentiment et si j'ay estè assez heureux pour y avancer quelque chose qui vous soit nouvelle et qui vous satisfasse.

Je suis de ceux qui vous honnorent le plus, Monsieur et demeure etc.

9) L'extrait en question est celui qui parut dans les Acta Eruditorum de juin 1688, comme il résulte de la phrase suivante de l'article: G.G.L. De Lineis opticis et alia (Acta Erud. janv. 1689, p. 36):
Inspicienti igitur Junium anni 1688 occurrit relatio de principiis Naturae Mathematicis Viri Clarissimi Isaaci Newtoni, quam licet a praesentibus meis cogitationibus longe semotam avide et magna cum delectatione legi’. Les ‘Principia’ eux-mêmes ne sont parvenus à Leibniz qu'à Rome pendant son séjour dans cette ville d'avril jusqu'en octobre 1689. Voir l'Appendice à sa lettre à Huygens du 13 octobre 1690.

10) On verra dans l'Appendice cité dans la note précédente, que Leibniz, quoique peu incliné à abandonner les tourbillons, a compris toute la portée de cette remarque. En effet, il y démontre que dans son système même le tourbillon harmonique est superflu, parce que la vitesse circulatoire qu'il imprimerait à la planète est identique ave celle qu'elle possède de soi-même en vertu de la loi de l'inertie et de l'effet de la force attractive.