Si l'on vouloit que le corps pesant commencast a se mouvoirGa naar voetnoot6) dans cette ligne depuis le repos; elle seroit impossible. Mais si le corps est supposè avoir quelque mouvement, quelque petit qu'il soit, comme par exemple celuij qu'il acquiert en tombant de la hauteur perpendiculaire ABGa naar voetnoot7) alors la ligne courbe BC, qui est telle que le cube de BD prise dans le diametre depuis le sommet BGa naar voetnoot8), soit egal au solide du quarrè de l'appliquée DCGa naar voetnoot9) et de la hauteur de 9/4 AB satisfera au probleme.
Mais outre cette ligne BC il y a une infinitè d'autres du mesme genre et aisées a trouver, [comme BE, BF, BG par les quelles ce mesme corps, tombè du point A, approchera encore egalement de l'horizon ainsi qu'il est requis, mais plus lentement que par BC]Ga naar voetnoot10).
Que si BD est double de BA, le temps de la descente par l'espace BC sera egal a celuy de la chute par AB.
H.D.Z.
Ces autres sont aisees a trouver, parce que par ex. si le poids tombe du point
| |
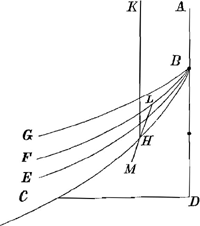
K egalement haut avec A, sur le point H de la courbe BHC, il est certain qu'il continuera d'approcher egalement du plan horizontal moiennant pourtant qu'il reflechisse en H contre un plan LM. Car il acquiert la mesme vitesse par KH que par ABH. Placant donc le point H en B et HK depuis B en haut, on aura une descente egale par HC transposée. Mais a fin que la chute viene de A, il ne faut que placer une courbe proportionelle qui ait le mesme raport à la longueur AB, que la courbe HC a la longueur KH. |
-
voetnoot2)
- Article VI de la livraison d'octobre 1687.
-
einda)
- Envoyée à l'autheur des Nouvelles, qui l'y a inserée. Octobr. 1687. nov. [Chr. Huygens].
-
eindb)
- Ces nouvelles n'avoient paru en public en cette ville que le 6 Nov. [Chr. Huygens].
-
voetnoot5)
- Dans les Acta Eruditorum du mois de mars 1686, Leibniz avait fait insérer l'article suivant:
G.G.L. Brevis demonstratio erroris memorabilis Cartesii & aliorum circa legem naturae, secundum quam volunt a Deo eandem semper quantitatem motus conservari; qua & in re mechanica abutuntur. Communicata in litteris d. Jan. 1686 datis.
Leibniz y démontra que ce n'est pas la force mouvante (vis motrix) ou la quantité de mouvement (quantitas motus), le produit de la masse par la vitesse, mais la force élévatrice (vis reassurgendi vel elevandi), le produit de la masse par le carré de la vitesse, qui se conserve dans la nature.
Ce principe avait déjà été énoncé longtemps auparavant par Huygens à l'occasion de ses lois du choc des corps durs; dans son Horologium Oscillatorium il s'en était servi comme base de sa théorie du pendule composé.
Dans le courant de son article, Leibniz, en faisant observer combien il était étrange que ni Descartes, ni les Cartésiens, viri doctissimi, n'avaient pensé à une démonstration aussi simple, s'était permis la remarque suivante: Quant aux Cartésiens, je crains que quelques-uns parmi eux ne commencent à imiter la plupart des Péripatéticiens qu'ils tournent en ridicule, c'est-à-dire qu'ils s'habituent à consulter, au lieu de la droite raison et de la nature des choses, les livres de leur maître. Leibniz termine son article en disant que l'erreur des Cartésiens a été la cause que quelques ‘viri docti’ avaient récemment mis en doute la règle Hugenienne des centres d'oscillation du pendule.
L'abbé de Catelan, Cartésien fervent, mis ainsi personnellement en cause (voir sa polémique sur les centres d'oscillation au Tome VIII), paraît avoir pris feu à l'occasion de cette réprimande. Il a fait insérer dans les Nouvelles de la République des Lettres du mois de septembre 1686 un article, précédé d'une traduction de l'article cité de Leibniz et intitulé:
Courte remarque de M. l'Abbé D.C. où l'on montre à G.G. Leibnits le paralogisme contenu dans l'objection précédente.
Leibniz a répondu par un article dans le numéro de février 1687; de Catelan a répliqué dans le numéro de juin, et la controverse s'est enfin terminée par un article de Leibniz dans le numéro du mois de septembre 1687 des Nouvelles de la République des Lettres. C'est à la fin de ce dernier article que Leibniz propose le problème, dont traite notre pièce, en ces termes: ‘J'adjouteray seulement, comme hors d'oeuvre, que j'accorde à M. l'abbé qu'on peut estimer la force par le Temps, mais c'est avec précaution. Par exemple on connoît la force acquise, par le temps que le corps pesant a mis à l'acquérir en descendant, pourvû qu'on sçache la ligne de desçente; car selon qu'elle est plus ou moins inclinée le temps changera: au lieu qu'il suffit de sçavoir [la hauteur du point de départ] pour juger de la force que le corps a acquise en descendant de cette hauteur. Or cette variété de temps m'a fait penser à un fort joli problème, que je viens de résoudre présentement & que je veux marquer ici, àfin que nôtre dispute donne quelque occasion à l'avancement de la Science: Trouver une ligne de descente, dans la quelle le corps pesant desçende uniformément, & approche également de l'horison en temps êgaux. L'Analyse de Messieurs les Cartesiens le donnera peut être aisément.’
-
eindc)
- Voyez le calcul de la Solution du Probleme, mis au net au livre G. [Chr. Huygens].
-
voetnoot8)
- L'imprimé a par erreur: le cube CD, perpendiculaire sur AB prolongée. La version correcte, que nous avons donnée dans le texte, n'a été inscrite qu'après coup dans le manuscrit, qui d'abord était identique avec l'imprimé.
-
voetnoot10)
- Au lieu des mots mis en parenthêses, l'imprimé a: qui feront le même effet; c'est-à-dire que le corps pesant après la chute par AB, descendant par ces lignes, approchera encore également de l'horizon en temps égaux, mais plus lentement que par BC.
|


