Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2490.
Christiaan Huygens.
[septembre 1690].
Appendice I au No. 2489.

La pièce se trouve à Leiden, coll. Huygens¹⁾.
Elle a été publiée par P.J. Uylenbroek²⁾.

Problema propositum a D. Leibnitz in diario Eruditorum (nouvelles de la République des Lettres) mensis Sept. 1687.

Solutionem, quae admodum extat in libro F versus finem³⁾, misi ad authorem diarii, qui eam inseruit mense Oct. ejusdem anni 1687. Vide quae hac de re habet

1) Dans le livre G des Adversaria, p. 47. D'après le lieu qu'elle occupe, elle doit avoir été écrite en septembre 1690. Elle représente probablement une rédaction plus soignée de la solution originale de 1687. Plus loin dans le même livre, p. 76, on rencontre une autre solution que nous reproduisons dans un second Appendice, le N^o. 2491.

2) Uylenbroek dans les Chr. Hugenii Exercitationes mathematicae, Fasc. II, n'a pas reproduit l'en-tête de la pièce. Sa rédaction commence par les mots: ‘Sit invenienda curva ACE.’

3) Voir la pièce N^o. 2489.

[p. 227]

Leibnitsius in Actis Erud. Lipsiensibus a.ⁱ 89 pag. 195⁴⁾ et aⁱ 90. p. 358⁵⁾. Itemque Bernoulius in iisdem Actis a.ⁱ 1690. p. 218⁶⁾.

Sit invenienda curva ACE, per quam devolutum grave corpus descendat aequalibus spatiis horizontem versus per temporis partes aequales.

Hoc fieri nequit incipiendo descensum a summo curvae puncto A, quia sive per rectam inclinatam ad horizontem, sive perpendicularem, semper, per prima tempora minima aequalia, erunt spatia peracta ut 1, 3, 5, 7, etc. Curvae autem minima particula tamquam recta censetur. Oportet itaque celeritatem aliquam mobili jam acquisitam priusquam ab A descendat. Ponatur ergo descendisse per BA.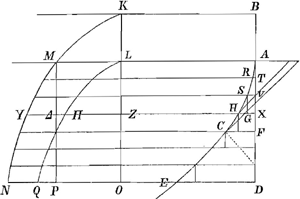

Et in perpend. AD intelligantur particulae aequales AT, TV, VX, XF etc., et ducantur ad curvam horizontales TR, VS, XH, FC, etc. Jam accipiendo particulas curvae AR, RS, SH, HC tanquam rectas, per quas mobile descendere pergat post casum per BA, peragi oportet has particulas temporibus aequalibus, quia sic mobile aequalibus intervallis horizontali plano appropinquabit. Peragentur autem tempo ribus aequalibus, si eadem proportione crescant earum longitudines, quâ augentur

4) Dans cet article d'avril 1689, Leibniz fit connaître sa solution du problème. Sur celle de Huygens il s'exprime en ces termes∶ Sed ejus loco (c'est-à-dire au lieu de l'abbé de Catelan auquel il s'était adressé plus particulièrement en proposant le problème du N^o. 2489) problema hoc sua opera dignum judicavit Vir celeberrimus Christianus Hugenius, cujus solutio meae prorsus consona extat in Novellis Reip. Literariae Octobr. 1687, sed suppressa demonstratione & explicatione discriminis inter diversas lineas ejusdem ut ait generis, quas satisfacere notat. Haec igitur ego supplere hoc loco volui, facturus citius, nisi aliquid a Domini Abbatis industria expectavissem’.

5) Ce dernier article ne contient, sur le problème en question, qu'une approbation de la solution donnée par Jacques Bernoulli dans les ‘Acta’ de 1690.

6) Voir la pièce N^o. 2491, note 1.

[p. 228]

celeritates, ut facile perspicitur. Sunt autem celeritates in punctis curvae singulis sicut ipsis respondentes applicatae in parabola KNM, posito vertice parabolae K eadem altitudine ac punctum B, et axe KO parallelo BD. Ergo et longitudines particularum curvae, AR, RS, SH, HC, eadem proportione crescere debent atque applicatae illae incipiendo ab LM. Sit MP parallela LO. Et referent partes aequales applicatarum, rectangulo MO inclusae, rectas omnes particulas AT, TV, VX, etc. ipsae vero applicatae in parabola integrae inter LM et ON, referent omnes particulas curvae, AR, RS, SH, etc. Eritque semper ut YZ ad ΔZ, quae aequalis ML, ita particula respondens curvae HC ad rectam XF, quia prima particula AR aequalis censetur AT, sicut applicata ML aequalis est lateri ML rectanguli MO. Sit SG perpend. in HX, similiterque a caeteris curvae intersectionibus in proxime subjectas horizontales ductae intelligentur perpendiculares. Jam cum sint inter se YZ ad ZΔ, sicut SH ad VX sive SG, erit et quadr. SG ad differentiam quadratorum SH, SG, hoc est ad quadr. HG, sicut quadr. ΔZ ad differentiam quadratorum YZ, ΔZ; sive ut quadr. ML ad differentiam quadratorum YZ, ML. Sit vertice L axe LO parabola LΠQ similis KMY, hoc est idem latus rectum habens, quae secet applicatam ZY in Π, erit jam quadr. ΠZ aequale differentiae quadratorum YZ, ΔZ sive quadratorum YZ, ML, ut facile ostenditur. Ergo erit jam quadratum ΔZ ad quadr. ΠZ, ut quadr. SG ad quadr. HG. Et proinde etiam ΔZ ad ΠZ longitudine, ut SG sive VX ad HG, atque ita omnes applicatae in parabola LΠQ referent omnes SV, HG, etc., sibi respondentes altitudine. Ideoque erit spatium semiparabolae LΠQO ad rectang. MO sicut omnes SV, HG, etc., hoc est recta ex iis composita ED ad rectam DA.

Sit BA vel KL = a. Latus rectum parabolarum r. Item AD = x. DE = y. Est ergo OQ = √rx, et spat. semiparabolae LQO = ⅔ rectang. LO, OQ, hoc est = ⅔ x√rx. Rectangulum vero MO = x√ar. Ergo ⅔ x√rx ad x√ar ut y ad x; unde 9/4 ay² = x³. Unde liquet curvam ACE esse paraboloidem, in qua quadrata applicatarum ad axem AD sunt ut cubi abscissarum inter applicatas et verticem A, cujus latus rectum = 9/4 BA.