Oeuvres complètes. Tome IX. Correspondance 1685-1690

(1901)–Christiaan Huygens– rechtenstatus



[pagina 573]
N^o 2644. Christiaan Huygens. [décembre 1690]. AppendiceGa naar voetnoot1) au No. 2643. La pièce se trouve à Leiden, coll. Huygens
§ IGa naar voetnoot2).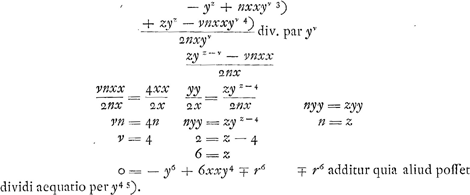 Ga naar voetnoot3)Ga naar voetnoot4) dividi aequatio per y⁴Ga naar voetnoot5).

[pagina 574]
§ IIGa naar voetnoot6). + y^z - πaay^v + θaaxx = 0 supposita aequ. curvae - zy^z + vπaay^v / 2θaax = s sed hic nullus terminus in numeratore ubi x extet. at erit si pro - zy^z ponatur ejus valor. - zy^z = - zπaay^v + zθaaxx 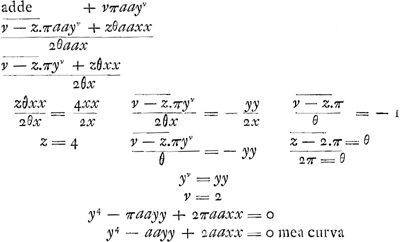Ga naar voetnoot7)
§ IIIGa naar voetnoot8).
[pagina 575]
Ergo eadem aequatio ad constructtionem, sive ponatur - y^z sen + y^z pro primo termino aequationis.
§ IVGa naar voetnoot9).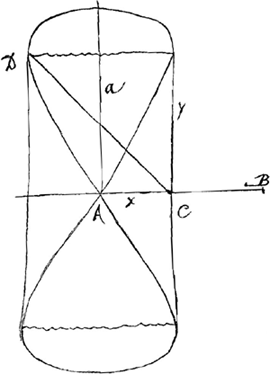 curva mea. reliqua pars meae. AB = a aequalis diagonali CD, tunc AC est maxima x. sive cum AC qu. aequatur ⅛ AB qu. y⁴ - aayy + 2aaxx = 0 mea curva yy = √¼ a⁴ - 2aaxx + ½ aa yy = a√¼ aa - 2xx + ½ aa xx non major quam ⅛ aa in mea curva semper aa major quam 8xx, aut si haec aequales, tunc yy = ½ aa.
[pagina 576]
Item yy semper major ½ aa et ½ aa major 4xx. semper yy major quam 4xx. Unde tangens semper eodem versus quo x sumendaGa naar voetnoot10). Leibnitsii curva. - y⁴ - aayy + 2aaxx = 0. 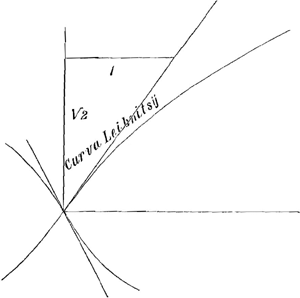yy = √¼a⁴ + 2aaxx - ½aa yy = a√¼aa + 2xx - ½aa yy = 3/2aa - ½aa hoc est y = a si a = x. mutatis + x in - x vel + y in - y manent aequationes eaedem. Ideoque curvae quadrifariam exeunt e principio unde sumitur x. Curva utraque eandem aequationem tangentis praebet sunt tamen constructiones diversae uti et ipsae curvae propter + y⁴ et - y⁴. In hac semper 2xx major quam yy, unde et in tangente, 4xx major yy, unde s in contrarium x sumenda, idque semper.	voetnoot1) Nous reproduisons dans cet Appendice, que nous avons divisé en paragraphes, plusieursendroits, empruntés aux pages 71 verso et 72 recto du livre des Adversaria G, qui se rapportent à la Lettre N^o. 2643 et qui peuvent servir à l'expliquer. voetnoot2) Ce paragraphe contient la détermination de la courbe dont la soustangente est donnée par l'équation s = yy/2x - 2x = yy - 4xx / 2x, c'est-à-dire l'intégration de l'équation ydx/dy = = yy/2x - 2x. voetnoot3) L'équation de la courbe cherchée est representée ici par - y^z + nxxy^v = 0, où les nombres z, n, v sont laissés indeterminés. voetnoot4) Valeur de la soustangente calculée au moyen de la régle (avec renversement pourtant du signe), que nous avons mentionnée dans la note 3 de l'Appendice N^o. 2612. voetnoot5) En effet, cette addition ne change pas la valeur de la soustangente. Consultez encore la note 3 de la Lettre N^o. 2639. voetnoot6) Détermination de la courbe dans le cas où la soustangente est donnée par l'équation s = - yy/2x + 2x = - yy + 4xx / 2x. voetnoot7) En effet, cette courbe est identique avec celle qui avait servi à Huygens à composer le problème qu'il avait posé à Leibniz (voir le § I de la pièce N^o. 2612). Pour s'en convaincre on n'a qu'à remplacer dans l'équation y⁴ - aayy + 2aaxx = 0 la valeur arbitraire aa par 8aa. voetnoot8) La courbe trouvée ci-dessus ne pouvant pas s'identifier avec celle donnée par Leibniz, Huygens en cherche la raison. A cet effet, il reprend le calcul du paragraphe précédent, en changeant seulement le signe du terme y^z et il arrive au résultat qu'un tel changement n'en entraîne aucun dans l'expression définitive de la soustangente. On voit facilement d'ailleurs que l'identification des deux solutions, celle de Huygens et celle de Leibniz, aurait pû être obtenue en remplaçant la valeur arbitraire aa par - aa; mais ce remplacement implique, comme Huygens ne manquait par de le découvrir, un changement radical dans la forme de la courbe. voetnoot9) Cette partie contient une comparaison entre les deux courbes, celle de Huygens et celle de Leibniz, aux équations: ± y⁴ - aayy + 2aaxx = 0. voetnoot10) Ce raisonnement ne s'applique qu'aux deux lunules ou demi ovales indiquées dans la figure par curva mea et renqua pars meae. En effet, quelque étrange que cela nous puisse sembler, accoutumés comme nous sommes aux conceptions modernes, il est certain que Huygens a commencé par méconnaître la continuité de cette partie de la courbe avec celle exprimée par yy = - a√¼aa - 2xx + ½aa. Bientôt il va reconnaître cette erreur, comme cela résulte de sa lettre à Leibniz du 23 février 1691, et c'est alors qu'il doit avoir ajouté dans la figure, que nous avons reproduite ici et dans celle du § I de la pièce N^o. 2612, la partie de la courbe qui manque dans la figure du texte de la lettre N^o. 2643.