Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 555]

N^o 2639.
G.W. Leibniz à Christiaan Huygens.
5 décembre 1690.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et par C.I. Gerhardt²⁾.
La lettre fait suite au No. 2636.
Chr. Huygens y répondit par le No. 2643.

A Hanover ce 25 de Novembre vieux style 1690.

Monsieur

J'apprehende de vous importuner trop souuent et d'interrompre vos pensées que j'estime pretieuses. Mais la raison qui me fait écrire maintenant, est que ma derniere, qui comme j'espere vous aura esté rendue maintenant, a besoin de suite pour satisfaire entierement aux deux problemes que vous m'aviés proposés. Je crois qu'il n'y a plus rien à demander³⁾ à l'egard de l'une des lignes proposées, ou DB⁴⁾ deuoit estre 2xxy - aax / 3aa - 2xy, car en ce cas, prenant les signes au pied de la lettre, comme vous les auiés exprimés, les lignes transcendantes, dont je vous ay envoyé l'equation, y satisfont parfaitement. Mais en cas qu'on veuille DB = = aax - 2xxy / 3aa - 2xy, la ligne que vous avés donnée vous meme y satisfait. Je viens

1) Chr. Hugenii Exercitationes Mathematicae, Fasc. I, p. 51.

2) Leibnizens Mathematische Schriften II, p. 64 et Briefwechsel p. 622,

3) Cette remarque semble indiquer que Leibniz, aussi peu que Huygens, n'avait pas encore fait l'observation que la solution complète d'une équation différentielle doit contenir nécessairement une constante arbitraire. Il est vrai que ses propres solutions contiennent souvent une telle constante, mais comme il se contente ici expressément de la solution particulière de Huygens, on en doit bien inférer qu'il n'avait pas encore entrevu la signification fondamentale de ces constantes.

4) Voir la figure de la Lettre N^o. 2633.

[p. 556]

à l'autre question, scauoir quelle ligne satisfait, DB devant estre yy/2x - 2x, ou bien 2x - yy/2x, car j'ai voulu chercher l'un et l'autre, afin qu'il ne manque rien, quelque interpretation que vous puissiés donner à vostre demande. Et il est à notre que les courbes encor icy sont toutes differentes selon qu'on change les signes, bien qu'il arrive icy, qu'elles deviennent toutes deux ordinaires, au lieu qu'auparavant le changement des signes a fait venir une ordinaire pour une transcendante. Je dis donc que lors qu'on demande DB = yy/2x - 2x, comme vous l'aviés proposé, l'equation de la courbe est 6a⁶xxy⁴ = a⁶y⁶ + r¹²⁵⁾, d'ou la dite valeur de DB viendra incontinent par le calcul ordinaire des tangentes. Mais lors qu'on demande DB = 2x - yy/2x, la courbe qui satisfait est assez differente de la precedante, et son equation est 2r⁴xx = r⁴yy + aay⁴⁶⁾, qui est moins elevée que l'autre de deux degrés. On peut varier la courbe en changeant la proportion de r à a. Ainsi j'espere maintenant de m'estre justifié un peu, et que vous reconoistrés, Monsieur, que j'ay eu quelque raison de m'attacher aux signes de la maniere que vous les aviés marqués vous même. Car suivant l'Analyse toute pure (comme il est necessaire de faire quand on veut chercher des solutions par son moyen) les signes doivent estre gardés tels que le calcul les fournit, sauf par apres à celuy qui fait la construction de mener la ligne CD comme il faut, selon que la valeur de DB est affirmative ou negative. Ces petits changemens sont quelques fois cause des beveues, sur tout en des methodes, ou l'on ne s'exerce pas souuent, comme il m'est arrivé en vous ecrivant ma derniere, ou le calcul que je vous ay envoyé touchant la relation entre les espaces et velocités, item entre les temps et les velocités est bon; mais la consequence que j'en auois tirée n'est pas bonne entierement. Car les temps estant t, espaces s, velocités v, la plus grande velocité a, il est vray comme j'ay marqué que les temps sont comme les sommes de a³ / aa - vv, et les espaces comme les sommes de aav / aa - vv. Mais au lieu d'en tirer cette consequence que les temps sont comme les logarithmes de √(aa - vv) et les espaces comme

5) La solution complète de l'équation différentielle y dx/dy = y²/2x - 2x s'écrit en effet:
6x²y⁴ = y⁶ + C.

6) La solution complète de l'équation y dx/dy = 2x - y²/2x s'écrit 2x² = y² + Cy⁴.

[p. 557]

les logarithmes de la raison de a + v à a - v, je deuois dire le contraire. Et



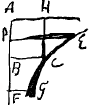peut-estre ne seriés vous pas faché, Monsieur, d'en voir la demonstration. Soit ECG l'hyperbole dont le centre A, le vertex C, les asymptotes AB, AH; et BC costé du quarré AC soit l'unité ou a dont le logarithme o. L'on scait que l'espace ou parallelogramme hyperbolique (comme vous l'appellés) BG sera le logarithme de AF, mais - BE sera le log. de AD, ou bien BE sera le log. de DE ou de 1/AD. Donc il est clair que BD ou BF estant v^a), alors BG ou le log. de 1 + v sera 1/1v - ½v² + ⅓v³ etc., et BE ou le log. de 1 / 1 - v sera 1/1 v + ½vv + ⅓v³ + ¼v⁴ etc. donc BG + BE ou le log. de 1 + v / 1 - v^b), sera 2/1v + ⅔v³ + ⅖v⁵ etc., ce qui est le double de la somme de a³ / aa - vv; mais BG - BE ou le log. 1 + v par 1 - v, c'est à dire le log. de 1 - vv sera - 2/2vv - 2/4v⁴ - 2/6v⁶ etc. Ou bien le log. de 1 / √1 - vv sera ½vv + ¼v⁴ + ⅙v⁶ etc. Ainsi √1 - vv estant en progression Geometrique decroissante, ½vv + ¼v⁴ + ⅙v⁶ (c'est à dire la somme de aav / aa - vv) seront en progression Arithmetique croissante. Cette methode servira en beaucoup d'autres rencontres; donc les velocités estant v, les temps seront les logarithmes de 1 - v/1 + v, et les espaces seront les logarithmes de √1 - vv. Ainsi ce que j'auois dit dans les Actes imprimés⁷⁾ n'a pas besoin de la correction que j'auois crû. Et l'equation exponentiale que je vous auois envoyée pour la relation des espaces et temps aura lieu, pourveu qu'on y change s en t et vice versa.

Je m'imagine que vous jugerès maintenant que les equations exponentiales n'ont rien d'obscur. Elles n'introduisent point de nouuelles lignes comme il semble que vous l'aviés pris, mais elles expriment mieux celles dont on a besoin, et les expriment d'une maniere au delà de la quelle il n'y a rien à pretendre. Aussi quand j'ay dit⁸⁾ que l'equation d'une certaine ligne est x³y/h = b2xy/., vous voyés bien maintenant que c'est comme si j'auois dit la nature de la ligne estre telle que x³y estant en progression Geometrique, 2xy ou meme xy sont en progression

a) BD ∞ BF ∞ v [Christiaan Huygens].

b) Log. rationis 1 + v ad 1 - v, quae est ratio DE ad FG [Christiaan Huygens].

7) Voir la Lettre N^o. 2632, note 10.

8) Voir la Lettre N^o. 2623.

[p. 558]

Arithmetique. On peut proposer de semblables problemes en nombres, par exemple soit x^x + x = 30, alors on satisfera faisant x = 3. Et ces problemes ne se peuuent construire geometriquement que par les lignes dont je me sers, lorsque les racines ne sont pas rationelles. Et je croirois auoir persectionné l'analyse, si je pouuois tousjours reduire les quantités transcendantes à un tel calcul. Et je seray bien aise de scauoir ce qui vous en semblera maintenant que le proces est asséz instruit pour que vous puissiés donner arret.

Vous reconnoitrés peut-estre aussi que je n'ay pas eu tant de tort de dire que ma maniere de calculer sert pour les problemes des tangentes données. Quand j'auois vu que vos deux lignes proposées estoient in potestate, je m'estois contenté d'en calculer l'une, qui venoit plus aisement, et j'attendois pour donner l'autre d'apprendre si elles pouuoient servir. Mais je voy que vous les aviés proposées tentandi gratia. Neantmoins j'ay esté bien aise de voir si je vous pourrois donner satisfaction, depuis que j'ay vu que la premiere n'auoit pas trouué une audience favorable. Cependant je ne me vante pas d'auoir poussé cette methode à sa perfection. Il s'agit sans doute de ce qu'il y a de plus profond et de plus difficile dans la Geometrie et dans l'Analyse. Mais je puis dire que je n'en suis pas fort eloigné et j'espererois d'en venir à bout si j'auois le loisir qu'il faut. Ce qu'il y a de beau entre autres, dans cette Methode, est qu'elle mene directement à des transcendantes, comme elle doit aussi, puisque ordinairement on y doit venir dans ces questions, à peu pres comme ordinairement les racines des equations sont sourdes. Mais lors que les courbes ordinaires peuuent satisfaire, les transcendantes memes le monstrent. J'ay une autre maniere particuliere⁹⁾ qui reussit toutes les fois que la courbe est ordinaire, mais je ne m'en sers pas volontiers à cause de sa prolixité. il faudroit faire des Tables pour la rendre aisée. J'estime bien plus la generale, mais je ne l'ay pas encor portée à sa perfection. Mais vous serés las de ces bagatelles. Il est temps que je finisse en me disant comme je puis faire avec beaucoup de zele et de sincerité

Monsieur

Vostre tres humble et tres obeissant serviteur Leibniz.

9) Allusion à la méthode mentionnée dans la Lettre N^o. 2627 et esquissée plus amplement aux pages 295 et 296 de l'article: ‘De Geometria recondita et analysi indivisibilium atque infinitorum’ publié dans les ‘Acta’ du mois de juin 1686.

[p. 559]

PS. Je vous envoyeray tout ce que jay promis¹⁰⁾ lors que je seray un peu plus en estat de mediter à des choses que je n'ay plus presentes dans l'esprit.

10) Nouvelle allusion à la pièce N^o. 2628, qui n'a jamais été envoyée.