Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 516]

N^o 2627.
G.W. Leibniz à Christiaan Huygens.
13 octobre 1690.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et par C.I. Gerhardt²⁾.
Elle est la réponse aux Nos. 2611 et 2623.
Chr. Huygens y répondit par le No. 2633.

Mr. Pendant que je vous prepare une lettre assés ample³⁾, tant pour m'acquitter de mon devoir, et pour vous remercier de l'honneur que vous m'avés fait en m'envoyant vostre excellent ouvrage, que pour profiter de vos instructions sur plusieurs points que vous avés touchés; voicy une troisieme lettre, qui m'arrive aujourdhuy, et qui me fait prendre la plume d'abord pour satisfaire par avance à une partie de ce que je dois, et pour vous dire, qu'il y a environ deux semaines, que le pacquet adressé par M. van der Heck s'est trouvé, et m'a esté rendu enfin. Ceux qui l'avoient receu en mon absence, ne s'en estant pas souvenus à mon retour, que lors que je l'ay fait demander.

Je conçois fort aisément, Monsieur, que vous avés une Methode equivalente à celle de mon calcul des differences. Car ce que j'appelle dx ou dy, vous le pouvés designer par quelque autre lettre, ainsi rien ne vous empeche d'exprimer les choses à vostre maniere. Cependant je m'imagine qu'il y a certaines vues qui ne viennent pas aussi aisement que par mon expression, et c'est à peu pres comme si au lieu des racines et puissances on vouloit toujours substituer des lettres, et au lieu de xx, ou x³, prendre m, ou n, après avoir declaré que ce doivent estre les puissances de la grandeur x. Jugés Mons. combien cela embarasseroit. Il en est de meme de dx ou de ddx, et les differences ne sont pas moins des affections des grandeurs jndeterminées dans leur lieux, que les puissances sont des affections d'une grandeur prise a part. Il me semble donc qu'il est plus naturel de les designer en sorte qu'elles fassent connoistre immediatement la grandeur dont elles sont les affections. Et cela paroist sur tout convenable, quand il y a plusieurs lettres, et plusieurs degres de differences à combiner, comme il m'est arrivé quelques fois, car il y a alors à observer une certaine loy d'homogenes toute particuliere, et la seule vue de-

1) Chr. Hugenii Exercitationes Mathematicae etc. Fasc. I, p. 32.

2) Leibnizens Mathematische Schriften, Bd. II, p. 49, et Briefwechsel von G.W. Leibniz, p. 600.

3) Voir l'Appendice à cette lettre, N^o. 2628

[p. 517]

couvre ce qu'on ne deméleroit pas si aisement par des notes vagues, comme sont des simples lettres. Je voy que M. Newton se sert des minuscules pour les differences⁴⁾, mais quand on vient aux differences des differences, et au delà, commè il peut arriver, il faudra encor changer, de sorte qu'il me semble qu'on fait mieux de se servir d'une expression qui s'etend à tout. Cependant quand on est accoustumé à une methode on a raison de ne la pas changer aisement, quoyque on conseilleroit peut estre à d'autres, qui n'en ont encor aucune, de se servir de celle qui paroist la plus naturelle. Aussi sans quelque chose d'approchant de mon expression, je ne scay si on s'aviseroit d'exprimer les courbes transcendentes comme la Cycloide ou la quadratrice, par des equations entre x et y abscisse et ordonnée, ou il n'entre aucune inconnue que ces grandeurs ou leur affections⁵⁾. Mais peut estre qu'il y a aussi quelques avantages dans vostre expression qui me sont encor inconnus, et je seray ravi d'en estre instruit, estant plus porté a prositer de vos lumieres, qu'à vouloir contester avec vous.

Je croy d'avoir trouvé les deux lignes que vous m'aviés proposées dans vostre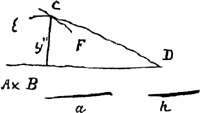



lettre de Voorbourg. Appellant AB, x, CB, y et DB devant estre 2xxy - aax / 3aa - 2xy je trouve x³y/h = = b2xy/.⁶⁾ où 2xy est l'exposant de la grandeur b⁷⁾. C'est une equation transcendente, ou les inconnues entrent dans l'exposant; h est une grandeur arbitraire, qui fait varier la courbe infinites fois; a est l'unité, et le logarithme de l'unité icy est o; et b est une grandeur dont le logarithme est l'unité. J'ay parlé quelques fois dans les Actes de Leipzig

4) Newton emploie cette notation dans le Lemma II, si bien connu, de la Sectio II, Liber secundus des Principia, où il expose le principe de sa méthode des fluxions.

5) Voir, sur ce passage, la Lettre N^o. 2601.

6) C'est ici le commencement du malentendu sur le signe de la soustangente dont nous avons parlé dans la note 3 de la pièce N^o. 2612. En effet, la solution de Leibniz, que l'on écrirait maintenant: x³y = C.e^2xy/a2, se rapporte à l'équation différentielle: ydx/dy(subt.) = 2x²y - a²x / 3a² - 2xy, tandis que le problème que Huygens avait en vue aurait conduit à l'équation:
y dx/dy = - 2x²y - a²x/3a² - 2xy, dont la courbe xy² - a²y + x³ = o, étudiée par Huygens dans la pièce citée, représente une solution particulière.

7) Les mots en italiques ont été ajoutés par Leibniz de sa propre main à la suite de l'équation répétée en marge de la lettre, laquelle est écrite d'une autre main que celle de Leibniz.

[p. 518]

de ces equations à exposans inconnus, et quand je les puis obtenir, je les prefere à celles qui ne se forment que par le moyen des sommes ou differences⁸⁾. Aussi peuvent elles estre toujours reduites aux equations differentielles, mais non pas vice versa. Je voudrois bien sçavoir si les lignes que vous m'avés proposées peuvent avoir quelque usage.

En considerant vostre chiffre de la ligne de la chaine pendante, j'y trouve quelque rapport à mon calcul, mais aussi quelque difference. Car au lieu de l'equation xxyy = a⁴ - aayy, je voy dans mon calcul reduit à certains termes, xxyy = a⁴ + aayy, qui sert à arriver à la ligne de question, et quoyque cette ligne soit du nombre des transcendantes, je ne laisse pas (supposita ejus constructione) d'en pouvoir donner⁹⁾ non seulement les touchantes, mais encor la dimension de la courbe, la surface du solide de sa rotation et la dimension de l'espace compris de la courbe et de l'axe; et le calcul m'offre tout cela comme de soy même. De la maniere que vous en parlés, Monsieur, je ne doute point que vous n'ayiez tout cela, et quelque chose de plus. Mais comme je me haste a present à vous repondre, je ne m'y arresteray pas presentement.

Je n'ay pas non plus que vous, Monsieur, raison d'estre trop content de Mr. D.T. car il m'est arrivé plus d'une foy qu'il a oublié d'avoir vu aupres de moy des echantillons des choses qu'il a données par apres. Je m'estois avisé de forger des courbes indeterminées, designées par une expression generale, comme a + bx + + cy + dxx + exy + fyy etc. = o et de determiner par ce moyen s'il est possible de trouver des quadratrices ordinaires des courbes données, c'est à dire s'il y a moyen de trouver une quadrature generale de la courbe donnée pour toutes ses portions. J'en avois dit quelque chose à M. Tschirnhaus, et je sus surpris de voir plusieurs années apres, qu'il en parloit comme de son invention dans les Actes de Leipzig¹⁰⁾. Par malheur il poussa sa methode trop loin, il s'imagina de pouvoir demonstrer par là encor les impossibilités des quadratures particulieres. Mais je luy donnay une instance, qui l'obligea à chercher des faux fuyans assés estranges, et qui n'auroient pas servi, si j'avois voulu le pousser¹¹⁾. J'avois aussi certaines notions

8) Leibniz veut dire qu'il préfère ces Equations à celles où l'on fait entrer des intégrales, comme dans celle qu'il avait indiquée pour la cycloïde dans sa lettre N^o. 2601, et aux équations différentielles.

9) La solution de Leibniz parut dans les Acta de juin 1691 sous le titre: De linea in quam flexile se pondere proprio curvat, ejusque usu insigni ad inveniendas quotcunque medias proportionales et Logarithmos.

10) Il s'agit de l'article dans les Acta d'octobre 1683, cité dans la Lettre N^o. 2324, note 19.

11) On peut consulter sur cette polémique les articles suivants de Leibniz, insérés dans les Acta Eruditorum, savoir: De di mensionibus figur arum inveniendis (mai 1684), Additio ad schedam in Actis proxime antecedentis Maji pag. 233 editam, de dimensionibus curvilinearum (déc. 1684), De geometria recondita et analysi indivisibilium atque infinitorum (juin 1686), la réponse de von Tschirnhaus, contenue dans l'article: Additamentum ad methodum quadrandi curvilineas figur as, aut earum impossibilitatem demonstr andi per finitam seriem (sept. 1687), et la correspondance privée de Leibniz et von Tschirnhaus de l'année 1683 (Gerhardt, Brieswechsel, p. 453-475).

[p. 519]

philosophiques, que j'ay remarquées depuis dans sa Medicina Mentis. Considerant, par exemple, autrefeis la demonstration pretendue de M. Des Cartes sur l'existence de Dieu, qui a esté inventée premierement par S. Anselme, je voyois que l'argument est effectivement demonstratif, quand on accorde que Dieu est possible. Cela me fit remarquer, qu'on ne scauroit se fier sur une demonstration lors qu'on n'est pas asseuré de la possibilité du sujet. Car s'il implique contradiction ce qu'on demonstrera de lui, pourra estre vray et faux en mesme temps. Cela me donna occasion de faire cette distinction entre les definitions reelles et nominelles, que les nominelles se contentent de nous donner moyen de discerner ou reconnoistre la chose definie, si elle se rencontroit; mais les reelles doivent faire connoistre de plus, qu'elle est possible. Et je jugeay aussi que c'estoit là le moyen de discerner les idées vraies et fausses; ne demeurant pas d'accord du principe de M. Des Cartes, que nous avons l'idée des choses dont nous parlons, lors que nous nous entendons. Sur cette reflexion, qu'il faut tacher de connoistre les possibilités de notions, Mr. D.T. a basti une partie de sa Medicina Mentis. Je luy envoyay aussi des remarques apres la publication de son ouvrage, où je luy fis voir, que sa regle de determiner les tangentes par les foyers ne pouvoit reussir que rarement, dont je luy donnay un exemple. Je remarquay aussi que son denombrement des lignes courbes de chaque degré ne va pas bien. Je me mis à chercher une meilleure regle pour determiner les tangentes par les foyers et filets et je la trouvay; mais pour la publication, j'ay esté prevenu par Mr. Facio Duillier¹²⁾, dont je ne suis pas fort faché; car il me semble, qu'il a bien du merite. Je vous diray pourtant ma maniere: j'avois trouvé et demonstré ce principe general, que tout mobile ayant plusieurs directions à la fois, doit aller dans la ligne de direction du centre de gravité commun d'autant de mobiles qu'il y a de directions, si on s'imaginoit le mobile unique multiplié autant de fois pour faire reussir entierement, et en meme temps chacune; et que la vistesse du mobile dans cette direction composée doit estre à celle du centre de gravité de la siction, comme le nombre des directions est à l'unité. Cela posé, je consideray que le stile, qui tend les filets, peut estre conçu comme ayant autant de directions (egales en vitesse entre elles) qu'il y a de filets.

12) Voir la pièce N^o. 2460.

[p. 520]

Car comme il les tire il en est tiré. Ainsi sa direction composée, qui doit estre dans la perpendiculaire à la courbe, passe par le centre de gravité d'autant de points, qu'il y a de filets; qui sont les intersections d'un cercle (décrit du point de la courbe) avec les filets. Mais il est temps de finir, et de me dire, comme je le puis et dois, avec toute la sincerité et toute la reconnaissance possible

Monsieur

Vostre treshumble et tresobeissant seruiteur Leibniz.

P.S. Ne continuerés vous pas, Monsieur, de nous donner quelque chose de temps en temps du grand nombre des belles pensées que vous avés? Ne fait on pas quelques découvertes en Hollande ou en Angleterre? Mons. Hudde ne songet-il plus aux sciences? Mons. Arnaud¹³⁾ est il en Hollande?

a Hanover ce 3/13 d'octobre 1690.

13) Antoine Arnauld, le célèbre janséniste. Il se trouvait alors à Bruxelles, où il mourut à l'âge de quatre-vingt trois ans, le 8 août 1694.