|
| |
| |
| |
No 2601.
G.W. Leibniz à Christiaan Huygens.
25 juillet 1690.
La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. UylenbroekGa naar voetnoot1) et par C.I. GerhardtGa naar voetnoot2).
Elle fait suite au No. 2512.
Chr. Huygens y répondit par le No. 2611.
Leibniz a Huygens.
Hanover 15/25 Juillet 1690.
Monsieur
Comme vostre temps nous est pretieux, je ne vous importunerois pas, si je ne trouuois à propos de vous recommander un jeune homme de tres grande esperance, nommé Mr. SpenerGa naar voetnoot3). Il s'applique fort à la physique, et puis qu'il joint la connoissance de la Chymie à celle des mathematiques, je m'en promets beaucoup. Comme il pretend l'honneur de vous faire la reverence à la Haye, vous en jugerés mieux, et il profitera de l'avantage de vous voir, pour se fortifier, dans ses bons desseins, et pour les poursuivre avec l'exactitude, qui y est necessaire. S'il venoit chez vous, je vous supplie de luy faire donner la cy-jointe.
Il n'y a que cinq ou six semaines que je suis de retour à Hanover d'un voyage de deux ans et plus, pendant le quel j'ay parcouru une bonne partie de l'Allemagne et de l'Italie pour chercher des Monuments Historiques par ordre de Monseigneur le Duc.
J'ay trouué bien peu de personnes avec qui on puisse parler de ce qui passe l'ordinaire en physique et en mathematiques. Mons. Auzout, que j'ai trouvé à Rome, nous promet une nouuelle edition de Vitruve, ou il pourroit bien reussir sans doute, puis qu'il a eu le moyen de voir tant d'antiques. Il pretend qu'il y a bien des passages ou Mr. PerraultGa naar voetnoot4) a debité plus tost ses propres pensées que celles
| |
| |
de l'auteur et des anciens. Mais je trouue que Mr. Auzout est trop distrait, et comme il ne veut pas donner des pieces detachées, j'apprehende que cela ne nous prive entierement du fruit de ses travauxGa naar voetnoot5).
J'ay trouvé aussi à Rome chez Mr. le Cardinal de BouillonGa naar voetnoot6), Mons. l'Abbé BerthetGa naar voetnoot7), que vous aurés peut-estre connu à Paris, sous le nom de P. Berthet, jesuite. Il s'applique fort à la musique, ou il fait des observations. Il est bon poëte avec cela, et il a traduit en Italien l'opera françois, qui s'appelle l'Amadis, et encore quelques autres, conservant parfaitement le meme chant, ce qu'on a trouvé beau et difficile. J'ay esté present à une representation qu'on en fit chez Mr. le Cardinal.
Le traité de Mr. Viviani de locis solidisGa naar voetnoot8) est imprimé en partie, mais comme il y manque encor quelque chose, il ne le monstre pas encore.
J'ay trouvé deux medecins, bien versés dans les Mathematiques, dont je me promets quelque chose, Mr. GuillelminiGa naar voetnoot9) à Bologne et Mr. Spoleti à Padoue.
| |
| |
J'ay la plus grande impatience du monde, Monsieur, de voir vostre traité de la lumiere, que j'attends de Hambourg, aussi tost qu'il y sera arrivé. Il y a déja longtemps que le public le souhaittoit. Il nous faut de tels liures pour avancer veritablement. J'attends d'y voir dechiffré le mystere du cristal d'Islande, et peut estre y trouverons nous quelque chose, qui puisse servir à deviner les raisons des couleurs, pour expliquer mathematiquement par quelle adresse la nature rend certaines liqueurs, ou surfaces, toutes rouges ou toutes bleues. Car je m'imagine que ces couleurs, qu'on appelle fixes, ne viennent pas moins de la refraction que celles qu'on appelle transparentes, quoyque feu Mr. de Mariotte ait esté d'un autre sentiment.
Je ne scay Monsieur si vous avés veu dans les Actes de Leipzig une maniere de calcul, que je propose, pour assujettir à l'analyse ce que M. Des Cartes luy mème en auoit excepté. Au lieu que les affections des grandeurs, qu'on employoit jusqu'icy en calculant, n'estoient que les racines et les puissances, j'employe maintenant les sommes et les differences, comme 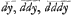 , c'est à dire differences et incremens ou elemens de la grandeur y, ou bien les differences des differences, ou les differences des differences des differences &c. Ga naar voetnoot10). Et comme les racines sont reciproques aux puissances, de mème les sommes sont reciproques aux differen- | |
| |
ces, par exemple, comme √ yy= y et ∛ y3= y, de même ∫ 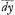 = y et ∫ 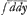 = y. Par le moyen de ce calcul je me suis avisé de donner les touchantes et de resoudre des problemes de maximis et minimis, lors que les equations sont fort embarassées de racines et de fractions, sans que j'aye besoin de les oster, ce qui m'epargne souuent des grandissimes calculs. Par le même moyen je reduis à l'analyse les courbes que M. Des Cartes appelloit Mechaniques, comme par exemple les Cycloides, exprimant par une equation la relation entre x et y abscisse et ordonnée
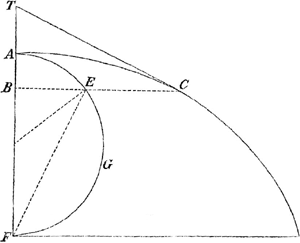
de la courbe. Par exemple AB le sinus versus estant x, alors FGE Ga naar einda) arc du cercle chez moy se designe ainsi ∫( a d x∶√2 ax- xx), c'est à dire l'arc est la somme des elemens de la courbe circulaire qui sont: a d x∶√2 ax- x2 (ou adx/√2 ax- x2 car les deux points me signifient division, pour eviter la soubscription du diviseur). C'est à dire les elemens de la courbe circulaire sont à dx elemens respondans de l'abcisse, comme a rayon est aux sinus versus Ga naar voetnoot11) √2 ax- x2. Cela estant posé, l'ordonnée de la Cycloide, menée perpendiculairement sur l'axe, que nous appellerons y, sera 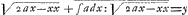 . Par le moyen de cette equation je trouue toutes les proprietés de la cycloide sans avoir aucun recours à la figure, comme si c'estoit une ligne ordinaire. Cherchant par exemple l'equation differentiale de cette equation, nous trouuons les tangentes de la cycloide; car 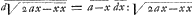 , par les regles de mon Al- | |
| |
gorithme, que j'ay données, donc dy = (2a-x) dx∶√2ax-x2 ou bien
dy∶dx∷2a-x∶√2ax-x2; c'est à dire dans la cycloide l'ordonnée est à la partie de l'axe comprise entre l'ordonnée et la touchante (ou bien dy est à dx), comme 2a-x, le sinus versus de l'arc parcouru FGEGa naar eindb) est au sinus rectus, c'est à dire CB à BT comme FB à BE. Ainsi l'analyse des lignes transcendentes estant établie, on pourra découurir bien des proprietés, dont on ne s'avisera pas sans cela et j'en ai beaucoup d'echantillons. Je souhaitte d'en auoir un jour vostre jugement dont je scay le poids. Je suis avec zele en vous souhaitant beaucoup de santé pour longues années
Monsieur
Vostre treshumble et tresobeissant serviteur Leibniz. |
-
voetnoot1)
- Chr. Hugenii Exercitationes Mathematicae, etc. Fasc. I, p. 23.
-
voetnoot2)
- Leibnizens Mathematische Schristen, Bd. II, p. 41, et Briefwechsel von G.W. Leibniz, p. 594.
-
voetnoot3)
- Johan Jacob Spener, Saxon. Nous avons de lui, dans la collection Huygens, une lettre datée du 29 août 1690.
-
voetnoot5)
- En effet, le projet d'Auzout n'a eu aucune suite.
-
voetnoot6)
- Emmanuel Théodose de la Tour, cardinal de Bouillon, né le 24 août 1644, favori de Louis XIV qui le nomma grand aumônier de France. Le roi l'envoya plusieurs fois à Rome pour des affaires diplomatiques. Son ingratitude et son opposition contre Louvois le firent bannir de la cour. Il quitta la France en 1710 et s'établit à Rome, où il mourut en mars 1715.
-
voetnoot9)
- Domenico Guglielmini, né à Bologne le 22 septembre 1655, mort à Padoue le 12 juillet 1710. Il fut inspecteur des canaux et professeur de mathématique et d'hydrométrie à Bologne jusqu'en 1698, puis professeur de mathématique, et en 1702 de médecine, à l'Université de Padoue.
Parmi plusieurs écrits d'astronomie et d'hydraulique il publia l'ouvrage:
Aquarum Fluentium mensura nova methodo inquisita. Autore Dominico Gulielmino M.D. Bononiensi, in patrio Archigymnasio Scientiarum Mathematicarum primario Professore, & aquarum Bononiensium Superintendente. Bononiae ex typographia Pisariana 1690. in-4o.
Au sujet de cet écrit il eut une longue controverse avec D. Papin. Elle commença par un article de ce dernier, inséré dans les Acta Eruditorum du mois de mai 1691 sous le titre:
Dion. Papini Observationes quaedam circa materias ad Hydraulicam spectantes Mensi Februario hujus anni insertas.
Guglielmini répondit par deux écrits, analysés dans les Acta Eruditorum de septembre 1692, savoir:
Dominici Guglielmini Medici et Mathematici Bononiensis Epistolae duae Hydrostaticae, altera Apologetica adversus Observationes contra Mensuram aquarum Fluentium a Clarissimo Viro Dionysio Papino factas, & Actis Erud. Lipsiae anni 1691 insertas: altera de velocitate & motu fluidorum in siphonibus recurvis suctoriis. Bononiae apud HH. Antonii Pisari 1692. in-4o.
Le second écrit fut la Pars Altera du premier ouvrage cité plus haut, publiée en 1691. La réplique de Papin se fit attendre jusqu'en 1695, lorsque parut son ouvrage:
Recueil de diverses Pieces touchant quelques nouvelles Machines. Cassel 1695, in-8o, paru également en latin sous le titre:
Fasciculus dissertationum de novis quibusdam machinis atque aliis argumentis philosophicis. Marpurgae. 1695. in-8o.
Dans cet ouvrage Papin a donné à sa réplique la forme d'une lettre publique à Chr. Huygens intitulée:
Lettre à Monsieur Christien Hugens Seigneur de Zulichem touchant la mesure des eaux courantes. Contre Mons. Dominique Guilielmini tres celebre Docteur en Medecine et Professeur en Mathematiques à Boulogne.
Epistola ad Illustrissimum Dominum Christianum Hugenium, Dynastam in Zulichem, de sluentium aquarum mensura, adversus Clar. Dominum Dominicum Guilielmini Medicum et Mathematicum Bononiensem.
Guglielmini avait cité Leibniz comme arbitre de cette controverse; Papin s'adressa à Huygens. Il ne paraît pas que les deux grands géomètres s'y soient beaucoup intéressés.
D'ailleurs il est douteux que Huygens, qui mourut le 8 juillet 1695, ait pu prendre connaissance de la lettre imprimée de Papin.
-
voetnoot10)
- Jusques là Leibniz avait publié dans les ‘Acta Eruditorum’ trois articles se rapportant à l'algorithme du calcul différentiel et intégral. Le premier, que nous avons cité dans la note 5 de la Lettre No. 2205, avait paru en octobre 1684. Le second, intitulé ‘De Geometria recondita et analysi indivisibilium atque infinitorum’, où le signe de l'intégration fut introduit pour la première fois, avait été publié dans les ‘Acta’ de juin 1686. Déjà dans le premier article, Leibniz avait indiqué l'usage qu'on pouvait faire des différentielles de second ordre, des ‘differentiae differentiarum’, pour distinguer entre les parties convexes et concaves d'une courbe donnée et pour déterminer ses points d'inflexion. Mais il en fit une application bien autrement importante dans son troisième article, celui de février 1689, cité dans la note 8 de la Lettre No. 2561, où il les employa pour former l'équation différentielle du second ordre, ‘aequatio
differentio-differentialis’ comme il l'appelle, qui lui servit à prouver que l'effort de la gravité dans une orbite planétaire doit être inversement proportionnel au carré de la distance.
-
einda)
- Voluit dicere AE pro eo quod dixit FGE [Christiaan Huygens].
-
eindb)
- Imo AE [Christiaan Huygens].
|
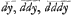 , c'est à dire differences et incremens ou elemens de la grandeur y, ou bien les differences des differences, ou les differences des differences des differences &c.Ga naar voetnoot10). Et comme les racines sont reciproques aux puissances, de mème les sommes sont reciproques aux differen-
, c'est à dire differences et incremens ou elemens de la grandeur y, ou bien les differences des differences, ou les differences des differences des differences &c.Ga naar voetnoot10). Et comme les racines sont reciproques aux puissances, de mème les sommes sont reciproques aux differen-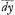 =y et ∫
=y et ∫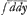 =y. Par le moyen de ce calcul je me suis avisé de donner les touchantes et de resoudre des problemes de maximis et minimis, lors que les equations sont fort embarassées de racines et de fractions, sans que j'aye besoin de les oster, ce qui m'epargne souuent des grandissimes calculs. Par le même moyen je reduis à l'analyse les courbes que M. Des Cartes appelloit Mechaniques, comme par exemple les Cycloides, exprimant par une equation la relation entre x et y abscisse et ordonnée
=y. Par le moyen de ce calcul je me suis avisé de donner les touchantes et de resoudre des problemes de maximis et minimis, lors que les equations sont fort embarassées de racines et de fractions, sans que j'aye besoin de les oster, ce qui m'epargne souuent des grandissimes calculs. Par le même moyen je reduis à l'analyse les courbes que M. Des Cartes appelloit Mechaniques, comme par exemple les Cycloides, exprimant par une equation la relation entre x et y abscisse et ordonnée

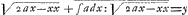 . Par le moyen de cette equation je trouue toutes les proprietés de la cycloide sans avoir aucun recours à la figure, comme si c'estoit une ligne ordinaire. Cherchant par exemple l'equation differentiale de cette equation, nous trouuons les tangentes de la cycloide; car
. Par le moyen de cette equation je trouue toutes les proprietés de la cycloide sans avoir aucun recours à la figure, comme si c'estoit une ligne ordinaire. Cherchant par exemple l'equation differentiale de cette equation, nous trouuons les tangentes de la cycloide; car 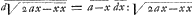 , par les regles de mon Al-
, par les regles de mon Al-
