Oeuvres complètes. Tome VIII. Correspondance 1676-1684
(1899)–Christiaan Huygens–No 2205.
| |
[pagina 249]
| |
cassée ou brisée un peu, y mêler ce petit morceau et le broyer avec la poudre, en se servant par exemple du plat d'un cousteau, avec le quel on le pressera contre la poudre sur une table, et la poudre s'allumera bien tost. On pourra écrire avec ce phosphore des lettres de feu, sur du papier, et on allumera ce papier en continuant de frotter ces deux experiences sont les plus commodes car on les peut faire sans consumer le phosphore. de fait en enfermant ce morceau, que je vous envoye a present, j'ay tracé des lettres lumineuses sur le papier tout comme on écrit avec de la craye ou du charbon, et je les ay pu lire tres clairement en cachant le papier au jour. Mais dans un lieu obscur elles paroissent et brillent merveilleusement avec quelque espece de mouuementGa naar voetnoot2). Si le papier s'en allume [au]Ga naar voetnoot3) la poudre s'allumera à plus forte raison. Je m'étonne que le premier a mangé la vessie et donné quelque atteinte au papier non obstant la cire qui l'entouroit. Maintenant j'ay couvert celuy-cy [dans]Ga naar voetnoot3) avec sa vessie de cire d'espagne. Je le vous envoyé, asin que vous ayés moins sujet de le ménager. Les essais que Mr. Becher a publiésGa naar voetnoot4) ne prouuent pas la realité de sa proposition, à moins qu'il fasse voir qu'on peut reiterer la même operation jusqu'à 50 fois avec le même argent. Car autrement, tout l'argent de l'Europe deuuroit passer par son fourneau, avant qu'il pourroit gagner la million promise par an. Je puis demonstrer que ce que j'ay [que j'ay]Ga naar voetnoot3) avancé suit de ma caracteristique lineaire ou Geometrique dont je vous ay envoyé un essay. Car premierement je puis exprimer parfaitement par ce calcul toute la nature ou definition de la figure (ce que l'Algebre ne fait jamais, car disant que x2 + y2 aeq. a2 est l'equation du cercle, il faut expliquer par la figure ce que c'est que ce x et y, c'est à dire que ce sont des ligne droites dont l'une est perpendiculaire à l'autre et l'une commence par le centre l'autre par la circonference de la figure). Et je le puis en toutes les figures, puis qu'elles se peuvent expliquer toutes par des spheriques, plans circulaires et droites dans les quelles je l'ay fait. Car les points des autres courbes se peuuent trouuer par des droites et cercles. Or toutes les machines ne sont que certaines figures, dont je les puis décrire par ces caracteres; et je puis expliquer le changement de situation qui s'y peut faire, c'est à dire leur mouuement. Secondement, lors qu'on peut exprimer parfaitement la definition de quelque chose, on peut aussi trouuer toutes ses proprietés. Cette caracteristique servira beaucoup à trouuer de belles constructions, par ce que le calcul et la construction | |
[pagina 250]
| |
s'y trouuent tout à la fois mais je ne dis pas qu'on puisse encor trouuer par là les plus belles absolument. J'avoue cependant que ces raisonnemens ne touchent point et qu'on a meilleure grace de faire ces choses que de prouuer qu'elles sont faisables. Les racines irrationelles et la methode de Diophante, n'ont rien de commun avec cette caracteristique de la situation; aussi n'est ce pas par là que j'y pretends. L'analyse qui sert pour les problemes semblables à ceux de Diophante, est une affaire faite, et je suis satisfait de la methode en general quoyque je ne me sois pas encore amusé à chercher des abregés particuliers. Les quels aussi bien que les racines irrationelles generales des equations superieures demandent quelques Tables que j'ay projettées pour eviter un calcul qui seroit trop prolixe, même dans le cinquieme degré. Les mêmes tables serviront pour toute l'Algebre. Les quadratures et les figures dont les proprietés des tangentes sont données demandent une maniere de calcul toute particuliere, dont j'ay des essais curieux; et j'ay trouvé par là une regle pour les tangentes ex data figura, qui passe infiniment les methodes connues. Soit une equation quelconque exprimant la relation des ordonnées y aux abscisses x par exemple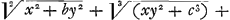 etc. aeq. etc. aeq. 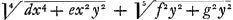 &c. ou quelque autre embarassée comme l'on voudra, je puis trouver les touchantes sans oster les irrationelles ny fractionsGa naar voetnoot5) (s'il y en a qui enferment x ou y) de l'equation. Car on ne les scauroit, sans enfler infiniment le calcul. Cet abregé estant si utile et presque necessaire dans les grands calculs, je le communiqueray quand il vous plaira. Je puis demonstrer que cette equation xx - x aequ. 24. est determinée, c'est à dire qu'elle a un nombre fini de racines. &c. ou quelque autre embarassée comme l'on voudra, je puis trouver les touchantes sans oster les irrationelles ny fractionsGa naar voetnoot5) (s'il y en a qui enferment x ou y) de l'equation. Car on ne les scauroit, sans enfler infiniment le calcul. Cet abregé estant si utile et presque necessaire dans les grands calculs, je le communiqueray quand il vous plaira. Je puis demonstrer que cette equation xx - x aequ. 24. est determinée, c'est à dire qu'elle a un nombre fini de racines.
Ma quadrature Arithmetique est mise au net, et demonstrée, je l'ay gardé pour l'Academie Royale, en cas qu'on puisse faire que l'auteur ait quelque relation avec elle, et qu'on juge alors ce traité digne d'estre mis par my d'autres bien plus importans qu'ils donnent. Son Altesse Serenissime mon maistre estant allée en Italie, j'auray un peu plus de loisir cette année, et je pretends d'achever ma machine ArithmetiqueGa naar voetnoot6). Je souhaitte fort de voir vostre Dioptrique, ou il y aura des choses importantes sans doute. Je voudrois scavoir ce que vous jugés du raisonnement de M. Des Cartes pour la regle des refractions, et de celuy de M. Fermat qui conclut la même | |
[pagina 251]
| |
chose par une supposition opposéeGa naar voetnoot7). La lettre de M. Fermat est la 51e. dans le 3me Tome de celles de Des Cartes, je ne suis pas satisfait de l'une ny de l'autre. Item si vous croyés que l'irregularité des refractions par exemple celle que M. Neuton a remarquéeGa naar voetnoot8) doit nuire considerablement aux lunettes. Je seray bien aise de voir vostre niveau. J'ay dessein de faire en sorte qu'on employe des moulins à vent aux mines du Harz qui appartiennent à mon maistre, pour en puiser l'eau sousterraine, qui empeche les travailleurs et qui s'en tire ordinairement par des moulins que l'eau venant de quelques ruisseaux et grands reservoirs fait agir. Mais l'eau manque souuent dans un temps sec la profondeur dont il faut tirer l'eau sousterraine est quelque fois jusqu'à 100 toises et plus. Je souhaitte vostre avis la dessus, et je suis avec zele
Monsieur
Vostre tres humble et tres affectioné serviteur Leibnitz.
P.S. J'ay marqué dans un papier à part ce que je croy bon d'observer chez M. Colbert, puisque vous avés la bonté, Monsieur, de vous y interesser pour moy.
P.S.Ga naar voetnoot9). Pour mieux reussir chez M.C. je croy qu'il seroit bon de dire qu'un Allemand curieux à envoyé ce phosphore, et qu'il en veut donner la composition, qu'il est versé en physique et mathematiques, qu'il offre sa correspondence pour communiquer de temps en temps des nouvelles decouvertes d'Allemagne et ayant beaucoup des connaissances pour apprendre qu'il peut même donner quelque chose de considerable du sien. Qu'il seroit peut estre a propos qu'il fut en quelque façon à l'Academie avec charge de correspondance et des appointemens en qualité de membre. Pour le nom il sera bon de ne pas dire sans necessité; ou même l'appeler Gottfredus Wilhelmi qui est aussi le veritable sans le nommer Leibniz. Car M.C. ayant eu souvent les oreilles battues de ce nom dans un temps qui n'y estoit pas propre, en sera rebuté s'il s'en souvient. Car les grands ayant une fois fait des difficultés sur une chose, ne se rendent pas aisement, et on reussit mieux en la proposant comme toute nouvelle. Si M. le Duc de Cheuvreuse et M. l'Abbé | |
[pagina 252]
| |
Gallois y prennent, il seroit bon aussi de les en avertir, à fin qu'ils ne donnent pas d'abord à connoistre à M.C. qu'on renouvelle une vielle solicitation. |
|

