Oeuvres complètes. Tome VII. Correspondance 1670-1675

N^o 2058.
Christiaan Huygens à G.W. Leibniz.
30 septembre [1675].

La lettre se trouve à Hannover, le sommaire se trouve à Leiden. Le sommaire a été publié par P.J. Uylenbroek et la lettre par C.I. Gerhardt.
Elle est la réponse au No. 2057.

Sommaire¹⁾:
Pour M. Leibnitz. Le principal sera de montrer la maniere d'extraire les racines quand il y a des quantitez imaginaire comme de 6 + √ - 1225/27, que c'est 2 + √ - ⅓, car assurement celle de Schoten n'y sert pas²⁾.
Bombellus ne dit pas par quelle methode il extrait cette racine. Il est vray qu'il le fait tentando, dans les cas ou il n'y a point d'imaginaires, mais il met encore une autre regle, dont je souhaite scavoir vostre pensée. La remarque est confiderable de la somme des racines √ (1 + √ - 1) + √ (1 - √ - 1) et autres telles, qui, nonobstant des quantitez imaginaires composent une quantité reelle.
Il faut demontrer clairement que toute aequation cubique rednisible a une racine rationelle.
Il faut aussi demontrer ce qu'il dit qu'on ne doit pas esperer des formules a ces aequations, ou il n'y ait point d'imaginaires.
Ses theoremes de sectione potestatum sont utiles. Et les racines qu'il donne par la de quelques aequations du 5e. et autres plus hauts degrez font voir partie de cette utilité mais ce seroit bien autre chose, si par leurs moyens il pouvoit donner des formules generales pour la solution de ces aequations.
L'instrument qu'il promet pour tirer les racines, selon ce qu'il me paroit, doit estre d'assez

1) Le sommaire de la lettre a été publié par Uylenbroek, comme une lettre séparée, le N^o. II de sa collection. Gerhardt a publié la lettre même, sous le même numéro, avec la date 30 septembre, sans millésime, d'après l'original de la bibliothèque de Hannover.
Le manuscrit de ce projet de réponse se trouve dans le livre E des Adversaria. Le lieu qu'il occupe confirme la date de 1675.

2) Il s'agit de la ‘Regula generalis extrahendi quaslibet radices ex quibuscunque Binomiis, radicem binomiam habentibus’, qui fait partie de l'Additamentum à la ‘Geometria’ de Descartes publiée par van Schooten, l'ouvrage cité dans la note 1 de la Lettre N^o. 150. Cette règle, en effet, ne s'applique qu'aux quantités réelles.

[p. 505]

difficile construction, mais apres avoir vû celuy d'arithmetique, que vous avez trouvè, je ne doute pas que vous n'en veniez a bout. Qu'il scait au reste que ces choses servent plus a faire voir la force de l'esprit et de la meditation que l'utilitè, parceque ces racines (comme disoit dernierement un de mes amis fort plaisamment) ne se mangent point.

Ce 30 Sept.

J'ay retenu plus longtemps que je ne devois, Monsieur, les escrits³⁾ que vous m'avez prestez, mais je crois que vous recevrez mes excuses quand je vous diray qu'ayant este fort longtemps hors d'exercice pour ce qui regarde ces sortes d'Equations Algebraiques, il m'a falu du temps pour les estudier de nouveau a fin de pouvoir juger de vos nouvelles inventions. Vous vous estes mis a chercher une chose qui doit estre bien difficile a trouver puis qu'elle ne l'a pas estè encore, qui est de donner des formules de racines pour les Equations du 5^e degrè et au delà. Et quoyque vous n'en serez pas encore venu a bout, c'est quelque chose d'avoir trouvè de ces racines dans beaucoup de cas, et d'avoir decouvert des Theoremes, qui semblent devoir faciliter le chemin aux regles generales.

Pour ce qui est de l'usage des racines de Cardan dans les cas mesme ou elles sont meslees de quantitez imaginaires, il est certain qu'elles servent tousjours dans les problemes d'Arithmetique, et vous avez plus fait que Bombelli en faisant voir que lors mesme que l'on ne peut pas tirer la racine des binomes, leur racines ne laissent pas de signifier des quantitez reelles. Mais a fin que l'on s'en puisse servir utilement il faut que vous nous donniez la methode que vous dites avoir trouvee pour tirer les racines de ces sortes de binomes tant au cas qu'elles sont extrahibles, qu'a ceux ou l'on ne les peut avoir que par approximation. Je vois que Bombelli en a extraict dans ces premiers cas, mais il y a apparence que ce n'a estè qu'en tastonnant, comme dans les autres extractions des racines cubes des binomes reguliers: quoyque il pretende d'avoir aussi quelque regle assurée pag. 151, de la quelle je seray bien aise d'entendre vostre avis.

Vous assurez une chose que je voudrois bien voir demontrée, sçavoir qu'il n'est pas possible de trouver des formules de racines sans quantitez imaginaires dans les cas ou la regle de Cardan produit de cette sorte de quantitez. La preuve de ces negatives est difficile. Pour ce qui est de celle de cette autre proposition importante que toute equation cubique qui peut estre deprimée contient une racine rationelle, il sera bon que vous fassiez voir comment elle suit de la realité des racines de Cardan dans tous les cas, car j'avoue que je ne le conçois pas encore clairement.

La remarque que vous faites touchant des racines inextrahibles, et avec des quantitez imaginaires, qui pourtant adjoutees ensemble composent une quantité reelle, est surprenante et tout a fait nouvelle. L'on n'auroit jamais cru que

3) Consultez les notes 6, 7 et 8 de la Lettre précédente.

[p. 506]

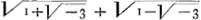fist √6, et il y a quelque chose de caché la dedans qui nous est incomprehensible⁴⁾.

L'instrument que vous promettez pour resoudre toute sorte d'Equations me paroit quelque chose de fort beau et je vous defierois d'en venir a bout si je n'avois veu desia ce que vous scavez faire par la machine d'Arithmetique⁵⁾. Je suis etc.

4) Leibniz, 27 ans plus tard, a cité ces paroles dans une lettre à Varignon. Voir, au Journal des Sçavants du Lundi 20 Mars m.dccii, l'article:
Extrait d'une lettre de M. Leibniz à M. Varignon, contenant l'explication de ce qu'on a raporté de luy dans les Memoires de Trevoux des mois de Novembre & Decembre derniers.

5) Voir la Lettre N^o. 1919, note 12.