Oeuvres complètes. Tome VII. Correspondance 1670-1675

[p. 500]

N^o 2057.
G.W. Leibniz à Christiaan Huygens.
[1675]¹⁾.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek²⁾ et par C.I. Gerhardt³⁾.
Chr. Huygens y répondit par le No. 2058.

Monsieur

Je vous envoye le liure de Bombelli⁴⁾, dont je vous ay parlé. Vous y verrez pag. 292 comment il se sert des racines imaginaires, (:il appelle par exemple √ - 121, ou 11 √ - 1, piu di meno 11; et - √ - 121 ou - 11 √ - 1 mene di meno 11:), et comment il trouue par la la racine de l'equation 1³ Π 15¹ plus 4, c'est à dire y³Π 15 y+4. Il dit d'en avoir une demonstration en lignes, qu'il met aussi pag. 298. mais il y prouue seulement qu'une telle equation est possible, et que sa racine

1) Cette lettre et la suivante ont été placées par Uylenbroek et Gerhardt en tête de la correspondance de Huygens et Leibniz. Ces éditeurs les ont donc jugées antérieures à celle du 7 novembre 1674, notre N^o. 1999. Toutefois, la preuve que les deux lettres en question appartiennent à la correspondance de 1675, nous paraît résulter, entre autres, de la lettre de Leibniz à Oldenburg datée du 27 août 1676, publiée par Gerhardt dans l'ouvrage décrit dans la Lettre N^o. 1919, note 12. On y lit (Tome I, p. 119): ‘De aequationum Radicibus Surdis Generalibus inveniendis, sive, quod idem est tollendis Aequationum potestatibus intermediis, multa et ego meditatus sum, et jam Vere anui superioris Specimina Hugenio communicaveram Regularum Cardanicis similium. Seriem enim habebam ejusmodi Regularum in infinitum euntem; in quibus et Cardanica continebatur. Sed ultra gradum cubicum non erant Generales. Perspexi tamen inde veram Methodum progrediendi longius.’
Quoique la Lettre N^o. 2057 ait donc précédé de quelques mois la réponse de Huygens, le N^o. 2058, nous avons cru ne pas devoir les séparer.

2) Christiani Hugenii aliorumque seculi XVII virorum celebrium Exercitationes Mathematicae et Philosophicae. Ex manuscriptis in Bibliotheca Academiae Lugduno-Batavae servatis edidit Petrus Joannes Uylenbroek, in eadem Academia Physices et Astronomiae Prof. Extraord. Fasciculus I, continens Chr. Hugenii, Leibnitii et Hospitalii Epistolas mutuas. Fasciculus II, continens Additamenta ad Fasc. I, inter quas Vaumesii, Duilierii et Hub. Huighenii Epistolas. Hagae Comitum, Ex typographia regia. mdcccxxxiii. 2 fasc. in-4^o.

3) Dans l'ouvrage cité dans la Lettre N^o. 1919, note 12. Dans cette correspondance nous suivons, pour les lettres de Huygens, le texte publié par Gerhardt d'après les originaux conservés à la Bibliothèque de Hannover.

4) Rafaele Bombelli, né à Bologna, mathématicien du 16me siècle, élève de Pier Francesco Clementi da Corinaldo. Il était ingénieur et travailla au dessèchement des Chiane en Toscane. Il est connu par son ouvrage:
L'Algebra parte maggiore dell' Aritmetica divisa in tre Libri: nuovamente posta in Luce, Bologna 1572. On trouve un extrait de ce livre au Tome III, pp. 363 et suivantes de l'ouvrage:
Histoire des Sciences mathématiques en Italie, depuis la Renaissance des Lettres jusqu'à la fin du XVIIe siècle, par M. Guillaume Libri, Membre de l'Institut. A Paris, chez Jules Renouard et Cie, Libraires Rue de Tournon, n^o. 6, 1838-1841, 4 Vol. in-8^o.

[p. 501]

est quelque chose de reel, qui se peut donner en lignes. Mais il ne s'ensuit pas que l'operation par son piu di meno est bonne. Car quoyque il dise à la fin de la page 294 que ces racines sont venues de l'equation ce n'est pas pourtant sans supposition. Il paroist aussi par la page 293. qu'il ne pouuoit pas resoudre par cette methode l'equation y³ Π 12 y + 9, dont la racine rationelle est fausse ou negative, sçavoir - 3. Il trouve neantmoins en essayant, par une autre methode (: tirée aussi de Cardan:) que l'equation se peut diviser par y + 3, ne scachant pas que par cette même raison - 3 en est la racine fausse: et il trouue par ce moyen la vraye 1½ + √ 5¼ la quelle estant composée d'un nombre et d'une racine quarrée ne pouuoit pas estre tirée des formules de Cardan: parce que les racines qu'on a par ces formules sont tousjours ou irrationelles cubiques ou nombres. D'ou vient qu'il a crû que les formules de Cardan ne servent pas en cette rencontre, et ne sont pas generales.

Ainsi je croy d'avoir demonstré le premier (1) que les formules de Cardan sont absolument bonnes et generales, soit extrahibles, soit non extrahibles; soit vrayes, soit fausses ou negatives (2) que nous avons par ce moyen la resolution generale de toutes les equations cubiques. (3) J'ai trouvé le premier qu'on peut former des racines composées non extrahibles de tous les degrez pairs, qui contiennent des imaginaires, et dont neantmoins la realité peut estre renduë palpable sans extraction: pour faire juger que la realité de telles formules n'est pas bornée par l'extrahibilité: dont l'exemple de la formule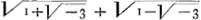 qui vaut √6, est une preuue tres considerable (4) je demonstre, ce que personne a demonstré encor, que toute l'equation cubique qui peut estre deprimée contient une racine rationelle pourveu que l'equation même soit proposée en termes rationaux. D'ou il s'ensuit que celle qui ne peut estre divisée par l'inconnue + ou - un diviseur rationel du dernier terme, est solide. Proposition tres importante, puisqu'elle nous donne un moyen asseuré de scavoir si un probleme est solide en effect ou s'il l'est seulement en apparence. Monsieur Des Cartes ne parle pas si positivement, car il dit⁵⁾, qu'il faut examiner toutes les quantités qui peuuent

5) Dans sa ‘Géométrie’, Livre troisième, Descartes, à propos des équations cubiques, s'exprime comme il suit: ‘Puis examinant par ordre toutes les quantités qui peuvent diviser sans fraction le dernier terme, il faut voir si quelqu'une d'elles, jointe avec la quantité inconnue par le signe + ou -, peut composer un binôme qui divise toute la somme; et si cela est le problème est plan,....Mais lorsqu'on ne trouve aucun binôme qui puisse ainsi diviser toute la somme de l'équation proposée il est certain que le problème qui en dépend est solide.’ Voir, aux pages 399 et 401 du Tome V, OEuvres de Descartes, publiées par Victor Cousin. A Paris, chez F.G. Levrault, libraire rue des Fossés-Monsieur-le-Prince, N^o. 31; et A Strasbourg, rue des Juifs, N^o. 33. m.dccc.xxiv à m.dccc.xxvi. 11 Vol. in-8^o.
Ainsi donc, Descartes n'exclut pas explicitement les facteurs a ± √a² - b², qui divisent, sans fractions, un nombre b. Toutefois, les exemples qu'il apporte prouvent qu'il n'a en vue que les facteurs rationels.

[p. 502]

diviser le dernier, qu'il suppose estre un entier et rationel: et il semble qu'il n'ose pas dire, tous les nombres, ou toutes les quantitez rationelles. De sorte qu'il nous laisse en doute, s'il ne faut pas aussi examiner les diviseurs irrationels: soit qu'il n'avoit point de demonstration assez convaincante pour les diuiseurs rationels à l'exclusion des irrationels; soit qu'il n'ait negligé de parler plus exactement. De la vient aussi qu'on peut demonstrer en cinquieme lieu (5) par la seule analyse, sans aide de Geometrie, que toute l'equation cubique est possible, pourveu qu'elle soit conceue en termes possibles. De plus (6) l'obstacle qui a embarassé principalement la resolution des equations par racines irrationelles estant levé, ceux qui chercheront des formules pour les plus haut degrez, ne seront plus rebutez par la rencontre des irrationelles, au lieu que sans cela ils chercheront envain des expressions differentes de celles qu'ils ont deja trouuées. D'ou vient que des personnes fort habiles en ces matieres ont crû avant cela qu'on ne scauroit trouuer une expression generale pour tout un degrez: persuasion qui les obligeroit à examiner inutilement toutes les formules, et toutes les combinaisons possibles des irrationelles, pour chercher des expressions particulieres pour certains cas qui semblent n'estre pas compris dans la generale. (7) Lorsqu'on aurait trouué les racines irrationelles des equations, tous les problemes qui peuuent estre reduits à une equation reviendront seulement à deux problemes de Geometrie, sçavoir à la section de l'angle, et à celle de la raison. J'entends par la section de la raison, ou si vous voulez, des Logarithmes, qui répondent en quelque façon aux arcs; l'extraction des racines. (8) Vous connoistrez mieux tout ceci par l'écrit⁶⁾, que je vous ay fait voir, et vous jugerez par les autres, que vous avez veu de même, de ce que j'appelle section des puissances, et de cette Table de Theoremes, qui peut estre continuée à l'infini, et qui a de grands usages, tant pour resoudre quelques equations affectées, que pour donner des abregez considerables dans le calcul, lorsqu'il s'agit de purger une equation des quantitez irrationelles, et de calculer par les puissances des grandeurs composées. Et comme ces theoremes donnent aussi la resolution de quelques formules des equations affectées de tous les degrez à l'infini, vous trouverez en (9) lieu, que c'est la premiere fois qu'on donne la resolution de quelques equations indeprimables plus que solides, par les irrationelles de leur propre degrez, puisqu'on n'en a pas encor trouué aucun exemple dans le 5^me de-

6) Les propositions 1 à 7, formulées ici par Leibniz, se retrouvent toutes dans le manuscrit de la bibliothèque de Hannover, publié par C.J. Gerhardt dans son ouvrage cité, Zweite Abtheilung, Tome III, p. 138-154, sous le titre:
De resolutionibus aequationum cubicarum triradicalium; de radicibus realibus, quae interventu imaginariarum exprimuntur, deque sexta quadam operatione arithmetica.
Il n'est nullement improbable que cet écrit, composé par Leibniz, comme il le dit, quelques mois après sa découverte de la vraie nature des formules de Cardan, est identique avec celui mentionné dans la lettre à Chr. Huygens.

[p. 503]

gré seulement, bien loin d'avoir donné une table, qui passe par tous les degrez à l'infini, comme j'ay fait⁷⁾.

Enfin, il n'y a personne, qui puisse mieux juger que vous de la qualité de deux inventions que je n'ay pas encor expliquées, qui sont (10) l'une de la Methode de tirer en nombres veritables ou approchans, les racines des binomes, ou il entre des imaginaires: et l'autre du compas des equations, qui donne sans aucun calcul, tout à la fois, toutes les racines d'une equation proposée de quelque degré et de quelque formule d'un degré donné qu'elles puissent estre; soit geometriquement en lignes soit arithmetiquement en nombres approchans, dont on peut incontinent tirer les veritables s'il y en a, sans aucun calcul. Il semble qu'apres cet instrument⁸⁾ il n'y a quasi plus rien à desirer pour l'usage que l'Algebre peut ou pourra avoir dans la méchanique et dans la practique. Il est croyable que c'estoit le but de la Géometrie des anciens, (: au moins de celle d'Apollonius:) et la fin des lieux qu'ils avoient introduits; par ce qu'ils avoient reconnûs que peu de lignes determinent en un instant ce que de grands calculs en nombres ne scauroient faire, qu'apres un long travail, capable de rebuter le plus ferme. Ils n'avoient pas poussé la chose fort loing: Mr. Des Cartes a suivi leur traces⁹⁾, et a donné une methode de digerer par ordre les courbes et de les accommoder aux problemes. Mais il ne s'y est pas pris de la maniere la plus simple et la plus naturelle pour ce qui est de les accommoder aux equations; d'ou vient que pour ces sursolides par exemple, il aura déja besoin quasi d'autant d'instrumens differens qu'on luy proposera de problemes. J'ay eu le bonheur de rencontrer le chemin que la nature semble avoir fait exprés. Les constructions s'y font sans calculs, et sans autre preparation que celles de changer les ouvertures des parties d'un meme instrument; le quel, à raison de sa grandeur, sert à toutes les equations imaginables.

Vous m'exhortez, Monsieur, de publier ces pensées et quelques autres, que vous avez veu de moy, du temps passé. Si vous témoignez d'estre encor de cette

7) Pendant son séjour à Paris, Leibniz, en collaboration avec von Tschirnbausen, s'est beaucoup occupé de la question de la résolution générale des équations algébriques. Plusieurs manuscrits de la bibliothèque de Hannover en témoignent encore. Consultez
Die Leibniz-Handschriften der Königlichen öffentlichen Bibliothek zu Hannover. Beschrieben von Dr. Eduard Bodemann Königl. Rath und Ober-Bibliothekar. Hannover und Leipzig. Hahn'sche Buchhandlung. 1895. in-8^o.
Toutefois, revenu plus tard des illusions qu'il s'était formées au commencement de ses recherches, il n'en a rien publié.

8) Un des manuscrits de la bibliothèque de Hannover porte le titre:
Constructor, Instrumentum algebraicum pro inveniendis omnium aequationum radicibus geometrice pariter et in numeris quantum libet exactis sine calculo.
Cet écrit contient la remarque suivante: ‘Inveni mense Decembr. 1674. Parisiis. Gottfredus Guilielmus Leibnitius.’

9) Dans le livre troisième de la ‘Géométrie’.

[p. 504]

même opinion, j'y travailleray tout de bon, et le sentiment que vous en avez me tiendra lieu d'approbation generale, dont je me flatte apres la vostre.

Au reste je suis

Monsieur

Vostre treshumble et tresobeissant serviteur Leibniz.