Oeuvres complètes. Tome VII. Correspondance 1670-1675

[p. 242]

N^o 1919.
Christiaan Huygens à H. Oldenburg.
14 janvier 1673.

La lettre se trouve à Londres, Royal Society.
Le sommaire et la minute d'une partie se trouvent à Leiden, coll. Iluygens¹⁾.
Elle est la répouse au No. 1914. H. Oldenburg y répondit par le No. 1924.

Sommaire:
du barometre. corrige 28½ pouces n'evapore point perpendicule a adjouter, qui ne doit pas estre parallele aux tuyaux.

A Paris ce 14 janvier 1673.

Monsieur

Je vous aurois fait responce dans le temps que je devois a deux de vos lettres²⁾, si des occupations un peu plus pressées qu'a l'ordinaire ne m'avoient emportè le temps ailleurs. Je vous rends graces de vos deux journaux et j'aurois eu soin de vous faire tenir le dernier de Monsieur Galois³⁾, si je ne croiois qu'on vous les envoie reglement, et qu'il ne faut pas vous charger deux fois du port d'un tel pacquet. Vous y aurez vu mes considérations sur Saturne⁴⁾ et la construction d'un nouveau barometre⁵⁾, dans la quelle il y a à corriger à la page 154 à la 4^e ligne, ou il faut lire de 28 pouces et demi ou lieu de 27½. Et a la mesme page ligne 4^e d'embas il faut mettre MN au lieu de BC, car pour la faute qui est dans la figure ou il y avoit un L au lieu de M, je crois que l'imprimeur l'aura fait corriger. Dans la pratique de ce barometre, qui reussit tres-bien, j'ay remarquè qu'il est necessaire sur tout pour mesurer des hauteurs, d'adjouter un perpendicule à la planche qui porte le barometre parce qu'il importe fort qu'il soit tousjours droit de mesme. Ce perpendicule est attachè par en haut, et passe en bas par un petit trou de cette largeur O, du quel on juge facilement quand il occupe le milieu. Pour ce qui est de l'huile que j'ay dit qu'on pourroit mettre sur l'eau je ne le trouve pas necessaire jusqu'icy, ayant experimentè que l'eau contenue dans un tuyau si long et si estroit, ne s'evapore aucunement, au moins pendant cette saison de l'année⁶⁾.

J'ay veu⁷⁾ comme Monsieur Newton prend peine a soutenir sa nouvelle opinion touchant les couleurs. Il me semble que la plus importante objection qu'on luy fait

1) Livre D des Adversaria, page 370.

2) Nous n'en connaissons qu'une après la lettre de Huygens du 27 septembre, N^o. 1912.

3) Le Journal des Sçavants du 12 décembre 1672.

4) Voir la pièce N^o. 1916.

5) Voir la pièce N^o. 1917.

6) La partie de la lettre qui va suivre, à l'exception des deux dernières phrases, a été traduite en anglais par Oldenburg et publiée, sans en indiquer l'auteur, dans les Phil. Trans. N^o. 96, du 21 juillet 1673 [V. st.] sous le titre:
An Extract of a Letter lately written by an ingenuous person from Paris, containing some Considerations upon. Mr. Newtons doctrine of Colors, as also upon the effects of the different Refractions of the Rays in Telescopical Glasses.
Elle est suivie, dans le N^o. 97, de la réponse de Newton, contenue dans la Lettre N^o. 1931.

7) Consultez l'article cité dans la Lettre N^o. 1914, note 2.

[p. 243]

en forme de Quaere est celle, s'il y a plus de deux sortes de couleurs? Car pour moy je crois qu'une hypothese qui expliqueroit mechaniquement et par la nature du mouvement la couleur jaune et bleue suffiroit pour toutes les autres parce que celles cy estant seulement plus chargees (comme il paroit par les prismes de Monsieur Hook)⁸⁾ produisent le rouge et le bleu obscur, et que de ces quatre tout le reste des couleurs se peut composer. Je ne vois pas aussi pourquoy Monsieur Newton ne se contente pas des 2 couleurs jaune et bleu, car il sera bien plus aisè de trouver quelque hypothese par le mouuement qui explique ces deux differences que non pas pour tant de diversitez qu'il y a d'autres couleurs. Et jusqu'a ce qu'il ait trouuè cette hypothese il ne nous aura pas appris en quoy consiste la nature et difference des couleurs mais seulement cet accident (qui assurement est fort considerable) de leur differente refrangibilitè.

Pour ce qui est de l'autre, à scavoir la composition du blanc de toutes les couleurs ensemble il se pourroit faire que le jaune et le bleu seroient encore suffisants pour cela, ce qui vaut la peine d'estre essayè et il se peut par l'experience que Monsieur Newton propose de recevoir contre la muraille d'une chambre obscure, les couleurs du prisme et d'esclairer par leur lumiere reflechie sur un papier blanc. Il faudroit empescher les couleurs des extremitez scavoir le rouge et le pourpre de donner contre la muraille et laisser seulement les couleurs d'entre deux, le jaune verd et le bleu pour voir si la lumiere de celles cy seules ne feroit pas paroitre blanc le papier, aussi bien que quand elles esclairent toutes. Je doute mesme si l'endroit le plus clair du jaune ne feroit pas tout seul cet effect, et je l'essaieray a la premiere commoditè, car cette pensee ne m'est venue qu'a cette heure.

Vous voiez bien cependant Monsieur, que si ces experiences succedent, l'on ne pourra plus dire que toutes les couleurs sont necessaires pour composer le blanc et qu'il sera tres vraisemblable que toutes les autres ne sont que des degrez de jaune et bleu, plus ou moins renfoncez.

Au reste pour ce qui est de l'effect des differentes refractions des rayons dans les verres de lunettes, il est certain que l'experience ne s'accorde pas avec ce que trouve Monsieur Newton, car a considerer seulement la peinture distincte que fait un objectif de 12 pieds dans une chambre obscure, l'on voit qu'elle est trop distincte et trop bien terminée pour pouvoir estre produite par des rayons qui s'escarteroient de la 50^me partie de l'ouverture⁹⁾ de sorte que, comme je vous crois

8) Voir, sur ces prismes, l'article cité de Newton (note 7) à la page 5093 des Phil. Transactions.

9) Dans la discussion que Newton a eue au sujet de la théorie des couleurs, il importe d'observer qu'il s'est servi dans ses célèbres expériences d'un prisme de verre contenant probablement du plomb et dont le pouvoir dispersif était considérablement plus grand que celui des verres employés sur le continent. Les données que Newton fournit dans sa première communication (Phil. Trans. N^o. 80, du 19 février 1671/72) permettent de calculer les indices de réfraction n^r et n^v des rayons extrêmes de son spectre. On trouve n^r = 1,5314, n^v = 1,5619, d'ou n^v-n^r = 0,0305. Si l'on admet que le spectre mesuré par Newton était compris entre les raies B et le milieu entre G et H, les indices trouvés auraient dû être pour le crownglass, n^r = 1,5243, n^v = 1,5423, n^v-n^r = 0,0180; pour le flint de Fraunhofer: n^r = 1,6277, n^v = 1,6656, n^v-n^r = 0,0379. Le verre de Newton approchait donc du flint de Fraunhofer. C'était la cause du différend de Newton avec Lucas, professeur de Liège. Tandis que Newton soutenait qu'avec un prisme de 63^o 12′ la longueur du spectre devait être de 5 fois la largeur, Lucas certifiait qu'avec un prismc de 60^o, il n'avait pu atteindre qu'une longueur de 3 à 3½ fois la largeur. Les données de Lucas permettent de calculer pour le verre de son prisme, n^v-n^r = 0,015. On était tellement éloigné d'admettre que la qualité du verre pouvait être la cause de la différence, que Newton mit fin à la discussion par cette déclaration: ‘For I know, that Mr. Lucas observation cannot hold where the refracting angle of the Prism is full 60 degrees, and the day is clear, and the full length of the Colours is measured, and the breadth of the Image answers to the Sun's diameter. And seeing I am well assured of the truth and exactness of my own observations, I shall be unwilling to be diverted by any other Experiments, from having a fair end made of this in the first place.’ Voir Phil. Trans. N^o. 128, du 25 Sept. 1676 [V. st.].
Si, comme il est probable, les fabricants de lunettes anglais employèrent pour leurs objectifs une même espèce de verre que Newton pour ses prismes, on pourrait voir, dans la haute valeur du pouvoir dispersif de leurs verres, une cause de l'infériorité de leurs longues lunettes.

[p. 244]

avoir mandè desia cy devant la difference de la refrangibilité¹⁰⁾ ne suit pas peut estre tousjours la mesme proportion dans les grandes et petites inclinations des rayons sur les surfaces du verre. En passant ce costè du feuillet je commence a apprehender que je vous ennuie par de trop longs raisonnements. C'est pourquoy je n'adjousteray plus rien si non pour assurer que je suis parfaitement

Monsieur

Vostre tres humble et obeislant seruiteur Hugens de Zulighem.

Dans la disposition du barometre quand on y adjoute le perpendicule il y a encor cecy a remarquer qu'il ne faut pas que les tuyaux montants soient tout a faits perpendiculaires, mais environ en sorte que les deux boetes soient perpendiculairement l'une au dessus de l'autre parce que dans cette situation l'eau montera le plus haut dans le tuyau ce qui me surprit lorsque je n'en scavois pas encore la raison.

Monsieur Leibniz est parti d'icy pour Angleterre¹²⁾ et vous le verrez bientost qui vous montrera une ebauche de sa machine¹¹⁾ pour les multiplications de nombres qui est fort ingenieuse.

10) Consultez la Lettre N^o. 1890.

12) C'est pendant son séjour à Paris, en 1672, que Leibniz a en ses premières relations avec Huygens. Trois fois, dans ses écrits, il en a consigné ses souvenirs.
Dans son article sur la chaînette, inséré dans les Acta Eruditorum de Leipzig, Année 1691, pp. 435 et suiv., il dit: ‘Eram ego hospes plane in interiore Geometria, cum Lutetiae Parisiorum A. 1672. Christiani Hugenii notitiam nactus sum, cui certe viro, post Galilaeum & Cartesium, & has literas publice, & me in ipsis privatim plurimum debere agnosco. Hujus cum legerem librum de Horologio Oscillatorio, adjungeremque Dettonvillaei (id est Pascalii) Epistolas & Gregorii a S. Vincentio opus, subito lucem hausi, & mihi, & aliis quoque qui me in his novum norant inexpectatam, quod mox speciminibus datis ostendi.’
Un autre témoignage est plus explicite. Il a été publié pour la première fois par M. Gerhardt dans l'ouvrage suivant:
Leibnizens gesammelte Werke aus den Handschriften der Königlichen Bibliothek zu Hannover herausgegeben von Georg Heinrich Pertz. Berlin, Druck und Verlag von A. Asher & Comp. 1850. in-8^o.
dont il forme la Dritte Folge, avec le sous-titre:
Leibnizens mathematische Schriften herausgegeben von C.I. Gerhardt. 1655.
Au Tome III, p. 71, M. Gerhardt a imprimé la minute d'un post-criptum d'une lettre de Leibniz à Jacques Bernoulli, datée de Berlin, avril 1703. Dans la lettre envoyée, le post-scriptum a été remplacé par un autre. Dans la pièce, trouvée par M. Gerhardt parmi les manuscrits de Hannover, on lit:
Cum Parisiis appulissem anno Christi 1672, eram ego Geometra autodidactos, sed parum subactus, cui non erat patientia percurrendi longas series demonstrationum. Algebram Lanzii cujusdam puerilem, deinde Clavii puer consulueram; Cartesii implicatior visa erat. Videbar tamen ipse mihi nescio qua satis credo temeraria ingenii fiducia par et his faturus si vellem. Audebamque inspicere libros profundiores, ut Cavalerii Geometriam et Leotaudii amoeniora curviliniorum elementa, quae forte Novibergae inveneram, et similia quaedam plane sine cortice nataturus. Nam pene legebam ut Historias Romanenses. Interim quendam calculum mihi Geometricum fingebam, per quadratilla et cubillos incertis numeris exprimendis; ignarus haec omnia Vietam et Cartesium melius elaborasse. In hac pene dixeram superba Matheseos ignorantia ego historias et jura circumspiciebam quod illis studiis me destinassem. Ex mathesi jucundiora libabam Machinas inprimis cognoscere atque invenire amans; nam et Arithmetica mea Machina illius temporis partus erat. Cum forte Hugenius, qui plus credo in me quaerebat quam erat, exemplum mihi sui de Pendulis Libri recens editum pro humanitate sua attulit. Id mihi accuratioris Geometriae initium vel occasio fuit. Dum sermones caedimus, animadvertit me non satis rectam habere notionem centri gravitatis; eam ergo indicavit paucis; simul addidit Dettonvillaeum (hoc est Pascalium) talia egregie executum. Ego qui semper hoc habui eximium, ut essem mortalium docilissimus saepeque luce ex unius magni viri verbis pauculis hausta innumera mea meditata nondum matura delevi; statim arripere monita summi mathematici: nam quantus esset Hugenius facile perspiciebam. Accedebat pudoris stimulus quod visus essem rem talem ignorare. Itaque Dettonvillaeum peto a Buotio, Gregorium Vincentiadem ex Bibliotheca Regis, jam vero Geometriam acturus. Nec mora illos ductus Vincentii, illas ungulas a Vincentio coeptas, a Pascalio promotas, tum illas summas et summarum summas nataque diverse solida et resoluta, cum jucunditate spectabam; plus enim voluptatis quam laboris asserebant. In his eram cum forte incido in demonstrationem Dettonvillaei specie levissimam, qua probat dimensionem Archimedaeam sphaerae,



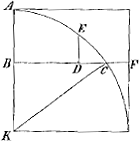
et ex triangulorum EDC et CBK similitudine ostendit, fore CK in DE = BC in E C, adeoque ponendo BF = CK, fore rectangulum AF aequale momento curvae AEF (AEC) ex axe AB. Haec ratiocinandi novitas me percussit; neque enim animadverteram apud Cavalerianos. Sed nihil magis obstupui, quam quod Pascalius fato quodam velatos oculos habuisse videretur; statim enim videbam generalissimum esse theorema pro quacumque curva, etsi perpendiculares in uno centro non concurrent, si modo perpendicularis a curva ad axem in ordinatam transferretur ut PC vel (P) (C) in BF vel (B) (F), manifestum erat zonam FB (B) (F) F aequari, momenta curvae C (C) ex axe.
Ego statim eo ad Hugenium, quem nondum revideram: dico me obsecutum esse ejus monitis,



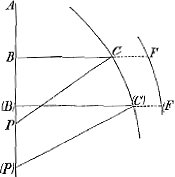
jam posse aliquid, quod neque Pascalius habuisset. Et theorema generale pro momentis curvarum expono. Ille admiratus, atqui, inquit, hoc ipsum theorema est, cui innituntur meae constructiones pro superficiebus Conoidum Parabolicorum, Ellipticorum et Hyperbolicorum explanandis, quae quomodo inventa essent Robervallius et Bullialdus nunquam sapere potuerunt. Itaque applaudens ipse progressibus meis, quaesivit, possemne jam curvarum quales FF naturas invenire. Cum negarem me in ea inquisitione exercitatum, ipse Cartesium et Slusium inspicere jussit, qui aequationes locales conficere docuissent, id enim ajebat esse percommodum. Ex eo Geometriam Cartesii examinavi, Slusiumque adjunxi, ingressus profecto in Geometriam per posticum.’
Enfin, on trouve un troisième récit de la première rencontre de Leibniz avec Huygens dans un ouvrage posthume de Leibniz, dont la publication est également due aux importantes recherches de M. Gerhardt, savoir:
Historia et Origo Calculi Differentialis a G.G. Leibnitio conscripta. Zur Zweiten Säcularfeier des Leibnizschen Geburtstages aus den Handschriften der Königlichen Bibliothek zu Hannover herausgegeben von Dr. C.I. Gerhardt. Hannover. Im Verlage der Hahn'schen Hofbuchhandlung. 1846. in-8^o. XIII et 50 pp.
Parlant de lui-même à la troisième personne, Leibniz y dit (p. 7):
‘Erat tunc ascitus in Revisionum Consilium Eminentissimi Electoris Moguntini, et a gratiosissimo, judiciosissimoque Principe (qui transiturum et longius iturum juvenem sibi vindicaverat) permissione continuandae peregrinationis impetrata, Lutetiam Parisiorum A.D. 1672 profectus erat. Ibi in Summi Viri Christiani Hugenii notitiam venit, cujus exemplo et consiliis se debere semper professus est aditum ad altiorem Mathesin. Is tunc forte suum de Pendulis opus edebat. Cujus cum exemplum juveni dono attulisset et inter colloquendum animadvertisset Centri gravitatis naturam huic non satis cognitam, quid hoc rei esset, et quomodo indagari posset, paucis exposuit. Id nostrum a veterno excitavit, talia a se ignorari indignum putantem. Sed tunc quidem vacare his studiis non potuit; et mox cum sub exitum anni in Angliam transfretavit in comitatu Legati Moguntini, ibique paucis septimanis cum Legato haesit, et ab Henrico quidem Oldenburgio, Societatis Regiae Secretario tunc, in illustre Collegium introductus est, cum nemine autem de Geometria contulit (in qua ipse tunc erat plane proletarius) etc.’ Et plus loin (p. 8):
‘Sed reversus ex Anglia in Galliam A.D. 1673 fatis interim functo Eminentissimo Electore Moguntino, cujus gratia Moguntiae obhaeserat, jam liberior hortante Hugenio coepit tractare Analysin Cartesii (antea vix eminus salutatam) et ut in Geometriam Quadraturarum introduceretur, Honorati Fabri Synopsin Geometricam, Gregorium a S. Vincentio et Dettonvillaei (id est Pascalii) libellum consuluit.’
Leibniz a écrit l'‘Historia’ environ une année avant sa mort. Ou remarquera que les trois récits accusent quelque confusion dans ses souvenirs par rapport à ce qui lui arriva lors de son premier séjour à Paris, en 1672, et après son retour en 1673. Ce n'est qu'en cette dernière année que Huygens a pu lui porter un exemplaire de son Horologium Oscillatorium. Ce détail, toutefois, ne peut que renforcer ce que Leibniz, dans l'‘Historia’, veut prouver par son récit, savoir, qu'au temps de son séjour de quelques semaines à Londres il était trop peu versé dans la Geométrie pour avoir pu s'intéresser à la méthode des fluxions, dont une malicieuse insinuation du Commercium Epistolicum l'avait accusé d'avoir dérobé le secret à Newton.
Dans le livre D des Adversaria de Huygens on lit à la dernière page: ‘1673. 30 dec. prestè a Libnisz mon livre de Circuli magn. et Gregorius de Vera Circuli quadr.’

11) Ce qui eut lieu le 22 janvier 1673 [V. st.].