Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 150.
Christiaan Huygens à Fr. van Schooten.
17 janvier 1653.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 149.

Schotenio.

Video me non satis dilucidè nuper exposuisse id quod de Curva linea Professoris Oxoniensis sentiebam quandoquidem persuadere Tibi non potui omnino irregularem, atque inordinatam eam esse, adeoque imperitè ab ipso hoc exigi, ut ex ijs quae proponit, perpendiculares 2^da, 4^ta, 6^ta, &c. exhibeantur, et qualis sit ipsa linea curva. itaque quaeso ut quae deinceps dicturus sum perpendere velis. Ostendi satis



manifestè atque id etiam te percipere scribis, lineam nullam eiusmodi in rerum natura existere, ut sumptis in contingente A7 partibus aequalibus A1, 1. 2, 2. 3 &c. magnitudinis arbitrariae, atque ductis usque ad curvam perpendicularibus ex punctis, 1, 2, 3, 4, 5 &c. prima sit partis unius, tertia 6, quinta 30 &c. Hoc itaque firmum atque indubitatum retinetur. Sed qualem nunc lineam ipsius ut imaginemur superest? Enimverò hoc unum, ut sumptis ab initio partibus aequalibus A.1, 1. 2, 2. 3, 3. 4 &c. ponatur in puncto 1 perpendicularis partis unius, in puncto 3. partium 6, in 5 partium 30 &c. et per terminos harum perpendicularium ducatur linea curva A.1.6.30. 140 &c. Et sane quidem, si per A et dictos perpendicularium terminos tantum una linea curva duci posset et non mille diversae, quaereret non immeritò quanta foret perpendicularis educta ex puncto 2. item ex 4. et 6. &c. Sed cum sint innumerae, apparet neque has perpendiculares 2^dam scilicet, 4^tam, 6^tam &c. determinatas esse, neque

[p. 218]

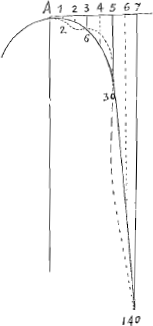
ulla puncta hujus lineae certum locum habere praeter ista 1, 6, 30, 140 &c. Itaque plane talem quaestionem propositam tibi credito. Datis quatuor aut quinque aut pluribus punctis per quae linea quaedam curva transit, dicere quaenam ista sit linea, et alia ipsius puncta designare. Quam sane quaestionem et determinatione et ratione prorsus carere facilè intelligis. Porro Trochoidem et Spiralem ne quidquam cum chimaeris hisce commune habere censeas, in ijs enim omnia puncta certum unumque locum obtinent licet geometrica ratione inveniri nequeant: adeo ut si in spirali unius revolutionis initium et duo alia puncta dentur, tota spiralis per haec determinata sit. Atque haec jam dicta sufficiant. Caeterum Trochoidis facta mentione venit in mentem, ut te interrogem, numquid in Commentarijs tuis Cartesianis, ubi demonstrationem tangentis ad hanc lineam adfers, per autorem (scriptum enim est in margine, Verba autoris.¹⁾) ipsum Cartesium intelligas, et an unquam demonstrationem Geometricam istius tangentis tibi ostenderit. Nimis eam videre vellem, et vix crediderim brevitatis gratia omissam si alioqui proba fuit. Videtur mihi Cartesius calculi Geometrici longè peritior extitisse quam demonstrationum efformandarum, aut inveniendae compositionis quo utroque tu excellis. atque illud nuperrimè etiam animadverti in problemate illo dioptrico quo per radium prismatis latera transeuntem docet proportionem refractionis invenire. Cum enim perpenderem cujusmodi illa demonstratio esse posset, quam à Gutschovio acutè inventam atque a te postmodum breviorem effectam dicebas, inveni ipsam constructionem à Cartesio allatam parum subtilem esse eamque ex ijs quae circa hanc materiam conscripta habebam sequenti modo contraxi demonstravique.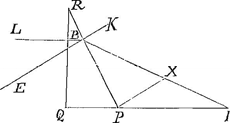

Triangulo BPI ut jubet Cartesius in chartam translato ducatur tantum PX ipsi PB ad angulos rectos, eritque PI ad IX proportio refractionis quaesita.

Productâ enim PB versus R secet eam EBK ad angulos rectos et ducatur BL parallela IP. Igitur LB radium refert qui postquam prismatis superficiem RQ penetravit absque refractione refringitur in B tenditque ad I. Et quia EBK in puncto B secat superficiem RP ad angulos rectos, constat proportionem refractionis eam esse, quam habet sinus anguli KBX ad sinum anguli EBL. Est autem angulo KBX aequalis angulus BXP, et angulo EBL aequalis angulus XPI, quia utrique horum si addatur angulus rectus constituunt angulos aequales LBP, BPI. Itaque et sinus anguli BXP ad sinum anguli XPI proportionem habet

1) Ces mots se trouvent à la page 227 de l'ouvrage suivant:
Geometria, à Renato Des Cartes Anno 1637. Gallicè edita; nunc autem cum Notis Florimondi de Beaune, in Curià Blaesensi Consiliarii Regii, in Linguam Latinam versa, et commentariis illustrata, operâ atque studio Francisci à Schooten, Leydensis, in Academia Lugduno-Batavâ, Matheseos Professoris, Belgicè docentis. Lvgdvni Batavorvm, ex officinâ Joannis Maire. cIƆIƆcxlix. in-4^o.

[p. 219]

eam quae est refractionis. Verum in triangulo PIX habet latus PI ad latus IX eam rationem quam sinus anguli PXI hoc est sinus anguli PXB ad sinum anguli XPI. Itaque patet habere PI ad IX proportionem refractionis, quod erat demonstrandum.

Remitto Tibi Nonancourtii libellum quem perlegi attentè; at hercule si non meliore successu in caeteris philosophatur, videtur mihi bonas horas male collocare. Alicubi non absimilia ijs profert quae Pater Gregorius a S^to. Vincentio circa Proportionalitates ratiocinatur quaeque eum in errores maximos abripuerunt. Sed fortassis ego haec non impune dixero, siquidem jam pridem parata εξετασεος meae refutatio Antwerpiâ nunciatur, autore Patre Ignatio ab Ainscom²⁾, Patris Gregorij discipulo. Praeterea alter quidam nobilis Bohemus³⁾ nuper Pragâ ad me literas⁴⁾ dedit, humanissimas equidem, sed quibus causam Antagonistae mei defendere conabatur. hunc vero ad meliorem mentem revocare conatus sum. Valde aveo rescire cujusmodi clarissimus Gutschovius sententiam laturus sit, qui nuper brevi epistola⁵⁾ aliam longiorem mihi promisit tum super his tum de alijs quibusdam rebus quas ex ipso discere concupiveram. Videtur autem optimus homo mirum in modum occupationibus distentus. Verum et Tu tuis non cares, ideoque jam te missum faciam. Optimae conjugi Tuae gratias maximas ages meo nomine, quod quaerendo annulo meo operam impendere dignata sit, quem sane ubi aperta epistola Tua conspexi, Samij Polycratis fortuna nihilo mea inferior visa est, cui annulum in mare abjectum e pisce capto excisum redhibitumque memorant.

Sed jam Vale, et sinito ut frequentiores à te epistolas impetrem.

17 Jan. 1653.

2) Il est question du Père François Xavier Aynscom, qui publia cet ouvrage en 1656.

3) A.A. Kinner a Löwenthurn.

4) Voir la Lettre N^o. 136.

5) Voir la Lettre N. 140.