earum mensurari posse, fuit Presbyter quidam Normannus, nomine de Vaumesle, cujus ea de re literas aliquot ad me datasGa naar voetnoot21) adservo.
Si antequam meus liber de Luce prodijt, errorem suum in curva describenda cognovisset D.T. jam ante quoque ipsum correxisset; nec totis 8 annis omnium reprehensioni expositum reliquisset. An Bernoulius fortasse eum animadvertit? Sed nihil invenio in Actis Lipsiensibus quo id appareat.
Asseverare ausim D.T. nullam hactenus demonstrationem habere legitimam descriptionis curvarum de qua pag. 71Ga naar voetnoot22) anni 1690. |
-
voetnoot2)
- Chr. Hugenii Exercitationes Mathematicae, etc. Fasc. II, p. 40.
-
voetnoot3)
- Il s'agit de la construction fausse de la catacaustique du cercle décrite par von Tschirnhaus dans l'article cité dans la Lettre No. 2274, note 4. Voici cette construction telle que von Tschirnhaus l'a formulée:
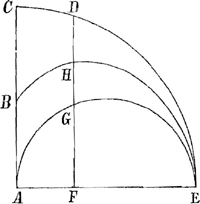
‘Sit data quarta pars Quadrantis CDE describatur Semicirculus AGE; hoc facto, ducatur linea quaecunque, veluti FD, parallela ad AC; tunc pars DG, intercepta intra quadrantem CDE et semicirculum AGE, secetur bifariam in puncto H; et sic praetendit Autor quod punctum hoc H sit aliquod ex infinitis, quae constituunt curvam BHE a radiis reflexis sormatam; ex quo sequitur, quod focus B debeat esse in loco medio radii AC’.
La courbe obtenue de cette manière possède en effet une ressemblance superficielle avec la vraie catacaustique du cercle dont Huygens avait montré le dessin à von Tschirnhaus et qui n'est autre, comme on sait, que l'épicycloide générée par le roulement du cercle décrit sur BC, comme diamètre, sur le cercle dont AB est le rayon et A le centre.
-
voetnoot4)
- Il s'agit, comme on verra dans la note 10 de cette pièce, de la page 93 du livre G, la page 97 verso de la pagination générale.
-
voetnoot5)
- La première entrevue entre Chr. Huygens et von Tschirnhaus eut lieu en 1675. Consultez la Lettre No. 2199, note 2.
-
voetnoot6)
- Voir les pages 123 et 124 de l'édition originale, où la nature épicycloidale de la courbe est indiquée dans le texte et même dans la figure par la présence du cercle décrit sur AC comme diamètre.
-
voetnoot7)
- C'est-à-dire la figure de von Tschirnhaus qui, en effet, est empruntée à la ‘Tabula XIX’ des ‘Acta’ de 1682.
-
voetnoot8)
- Il est intéressant de rapprocher de ce passage la lettre de von Tschirnhaus à Leibniz datée du 7 avril 1681 (Gerhardt, Der Briefwechsel von Leibniz, p. 414). Dans cette lettre, après avoir mentionné sa découverte prétendue de la catacaustique du cercle, von Tschirnhaus s'informe chez Leibniz si Huygens a trouvé quelque chose sur le mème sujet. Vellem scire, num talia ab aliquo Mathematicorum hactenus determinata, praecipue a Dr. Hugens, cujus Dioptrica nunc lucem forte vidit. Comme il est difficile de douter de l'assertion si positive de Huygens qu'il avait montré à von Tschirnhaus la figure de la catacaustique, on se demande, si c'est la mémoire ou la bonne foi qui faisait défaut à celui-ci, lorsqu'il écrivit ces mots.
-
voetnoot10)
- Ces lettres se rapportent à une figure qui se trouve à la page 97 du livre des Adversaria G, que nous reproduisons ici, avec la démonstration sur la même page de la non-identité des deux courbes.
Pour comprendre cette démonstration, il suffit de remarquer que la construction du point E, par laquelle elle commence, est conforme à celle indiquée dans le ‘Traité de la lumière’, au lieu cité dans la note 6.
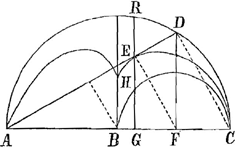
Arcus CD = 60o. Arcus AD = 2 DC. DE = ¼ subtensae DA. E est verum punctum curvae.
qu. GR = ▭ AGC. qu. GH = ▭ CGB. sed AG = 9BG, quia GF = ¼ FA, et FB = = ⅓ FA, unde BG = 1/12 AF etc.
Ergo qu. RG = 9 qu. HG.
Ergo HG = ⅓ RG. Quod si jam HR bifariam secta dicatur in E erit GE = HR = ⅔ GR. Jungatur EF, DC quae parallelae erunt quia DA ad AE ut CA ad AF. unde ang. AEF rectus, et qu. GE = ▭ AGF.
Ergo ▭ AGF = 4/9 qu. GR seu ▭ AGC. Ergo GF ad GC ut 4 ad 9 quod falsum, sunt enim ut 3 ad 7.
-
voetnoot11)
- La construction manquée de la catacaustique est précédée dans l'article cité dans la note 3, par les phrases suivantes:
‘Interim quia non sufficit, si quis observaverit saltem hinc lineas curvas’ (les catacaustiques) ‘sic formari, nisi et scientifice determinetur, cujus sint naturae: Methodum exhibet Generalem ope cujus curvae tales formatae ex intersectionibus radiorum reflexorum Geometrice possint determinari; et ut exemplum exhibeat Methodi hujus Generalis, in specie ostendit descriptionem Curvae illius, quae formatur a radiis solaribus in speculo ordinario sphaerico, hac ratione’: (suit la construction indiquée dans la note 3).
Consultez encore sur la méthode générale de von Tschirnhaus la note suivante.
-
voetnoot12)
- Les mots: quo deceptus fuit in hanc lineam inciderit manquent dans le texte d'Uylenbroek.
Gerhardt a publié (Briefwechsel, S. 428-436) un manuscrit de von Tschirnhaus qui contient la méthode par laquelle il prétend avoir trouvé l'équation fausse de la catacaustique et la construction (GH = HD, voir la figure de la note 3) qui s'en déduit. La méthode générale qu'il y expose est correcte et même ingénieuse, mais il reste au moins douteux si le résultat erroné auquel il arrive a été obtenu en effet, comme il le prétend, au moyen des éliminations embarrassantes auxquelles sa méthode le conduit, ou s'il est plutôt, comme Huygens le suppose, l'effet d'une conjecture hasardée, dont il veut faire passer le résultat comme ayant été obtenu par une méthode plus légitime.
-
voetnoot13)
- Allusion à la construction erronée de la tangente aux courbes à propriétés focales que von Tschirnhaus avait exposée dans sa ‘Medicina Mentis’. Consultez, sur cette construction et la polémique à laquelle elle a donné lieu, la correspondance de 1687. La dernière pièce qui s'y rapporte est notre No. 2486.
-
voetnoot15)
- Voir l'article: Methodus curvas determinandi, quae formantur a radiis reflexis, quorum incidentes ut paralleli considerantur, per D.T.
Dans cet article von Tschirnhaus commence par communiquer sans démonstration une formule générale pouvant servir à calculer la distance FE entre le point de réflexion E et le point correspondant F de la catacaustique d'une courbe quelconque, dont l'équation est
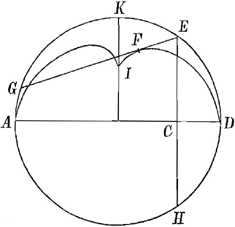
donnée. Cette formule est exacte, quoique inutilement compliquée. Il l'applique aux cas de l'hyperbole équilatère, du cercle et de la conique générale pour des rayons parallèles à l'axe.
Dans celui du cercle, sa formule conduit assez facilement à la relation FE = ½ y = ½ EC. Huygens, pour trouver le même point F, faisait l'arc EG égal au double de l'arc ED et GF = 3 FE. Il est facile de voir que les deux constructions reviennent au même et que von Tschirnhaus, en élaborant sa nouvelle méthode différente de celle mentionnée dans la note 12, s'est laissé inspirer bien probablement par le résultat de Huygens, qu'il connaissait d'avance. Aussi Huygens, d'après la liste de ses notes marginales, mentionnée dans la note 1 de notre No. 2540, écrivit-il, en haut de la page 72 de son exemplaire des Acta de 1690: ‘Hanc constructionem ex meo libro de Luce sumsit’.
-
voetnoot17)
- Voir la page 71 de l'article cité dans la note 15.
-
voetnoot18)
- Voir l'article intitulé: Curva geometrica, quae seipsam sui evolutione describit, aliasque insignes proprietates obtinet, inventa a D.T.
-
voetnoot19)
- Allusion à la propositio L, Sectio X, Liber primus des Principia: Facere ut corpus pendulum oscilletur in cycloide data. Dans cette proposition, sur laquelle on peut consulter encore la Lettre No. 2465, note 5, Newton démontre que la développée d'une hypocycloïde quelconque est une hypocycloïde semblable, et il était bien facile à prévoir que ce théorème resterait valable pour les épicycloïdes, notamment pour la catacaustique du cercle, dont von Tschirnhaus connaissait la nature épicycloïdale, soit qu'il l'eût reconnue, comme il le prétend dans l'article cité, par lui même, ou bien, comme il est plus probable, par la lecture du Traité de la lumière.
-
voetnoot20)
- En décembre 1678 et janvier 1679. Voir la Lettre No. 2145, note 6.
-
voetnoot22)
- Il faut lire probablement page 73. Huygens cite l'article de von Tschirnhaus, intitulé: Methodus curvas determinandi, quae formantur a radiis restexis, quorum incidentes ut paralleli considerantur, per D.T.
A la page 73 de cet article on lit le passage suivant, auquel Huygens probablement fait allusion:
Tandem notandum est, nullatenus opus esse, ut radii incidentes paralleli semper supponantur. Licet enim a quolibet puncto ad libitum assumto venire concipiantur, aut puncti loco quaevis curva assumatur, illi tamen qui haec, quae modo explicavi, nec non quae in Medicina mentis de curvarum formatione dicta sunt, bene intellexerit, neque hic aqua haerebit. Eadem via assumta refractionum mensura, determinabuntur Curvae, quae, a radiis refractis, corpora curva pellucida transeuntibus, generantur.
Von Tschirnhaus poursuit:
Quam innumera autem opticam perficientia inventa, eaque prorsus nova, hinc deduci possint, quamvis scientiae illi, hoc seculo ab ingeniosissimis viris admodum excultae, vix quidquam adjici posse videatur, periti harum rerum facile conjicient.
Dans la liste des notes marginales que Huygens a inscrites dans son exemplaire des Acta Eruditorum (voir la pièce No. 2540, note 1) on rencontre encore la suivante, écrite en marge du passage que nous venons de citer: vellem unum afferret.
|




