Oeuvres complètes. Tome VIII. Correspondance 1676-1684
(1899)–Christiaan Huygens–
[pagina 379]
| |
No 2274.
| |
[pagina 380]
| |
ciendi quae summas comburendi vires obtinere debent. Sed pestis quae tunc in vicinia grassabatur, impedimento fuit ad tale quid assequendum, dum interea hisce intentus essem se mihi modus obtulit, cujusvis generis et magnitudinis vitra sic expoliendi ut dubitem num praestantior exhiberi possit. Cum vero sic propositum meum continuo urgerem, tandem quod quaesiveram alia via obtinui. Construxi nempe speculum magnitudine excedens 48 pollices perfecte rotundum sine fusione et quod certe exiguo pretio et labore parari potest, licet multo adhuc majus esset, et quod tempore hiemali talia effecta in distantia septem quadrantum ulnae Lipsiensis exhibuit, quod nunquam speraveram. Interim artifex cui haec commiseram non ex voto aequalem undiquaque crassitiem huic speculo induxerat, ea etenim circa latera minuebantur; adeoque ipsa politura (quae etiam hic in singulari artificio consistit) non poterat tam perfecte exequi, circa exteriora quam interiora superficiei sphaericae. Alioqui sine dubio majores multo praestitisset effectus. Mandavi vero eidem artifici, ut hac hyeme speculum fabricaret quod et in majori distantia comburet, ut pote excedens 50 pollices, et spero me intuiturum insequenti aestate similes saltem si non majores vestri speculi effectus. Multum ergo circa specula caustica occupatus in hanc incidi speculationem. 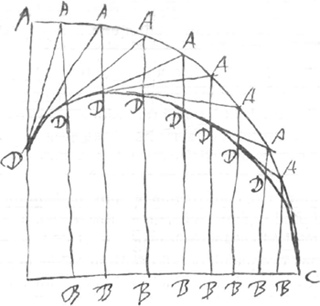 Sit circuli quadrans BAC, ac omnes lineae AB repraesentent radios solis in hanc curvam AC incidentes, sint et radij reflexi omnes AD. Quaeritur quam curvam DDD &c. horum radiorum reflexorum indefinitae intersectiones describant. Inveni autem curvam DDD esse geometricam prout D. des Cartes vocat. Deinde reperi quod data qualibet curva geometrica AAA, radij reflexi aut in unico concurrant puncto, uti fit in parabola, aut horum intersectiones curvas quoque geometricas efficient. Tandem quoque inveni generalem methodum data qualibet curva AAA, sive geometrica sive mechanica, quomodo curva hinc resultans DDD calculo determinari possit. Quantum hoc usum habeat inde manifestum erit, quod hac ratione, infinitae curvae in rectas mutari queant, et data quacunque curva geometrica hinc semper exhibeatur curva geometrica mensurabilis. Mirum hoc forte videbitur quod inter singularia solis effecta etiam hoc sit ut curvas in rectas transmutet: id quod tanto labore a mathematicis semper quaesitum fuit. Sed quod sol quaecunque ipsi opponatur superficies concava polita | |
[pagina 381]
| |
simile quid revera praestet constabit ex hoc generali theoremate, quod mathematicis credo haud ingratum erit. Est autem tale. Sit curva quaecunque AAA, sive geometrica sive mechanica aut etiam libera manu ducta. Formetur hinc curva DDD &c, quam radij reflexi parallelis incidentibus radijs, ut dictum, constituant. Dico lineam incidentem (uti sunt omnes BA) et reflexam (uti omnes AD) semper aequales esse curvae portioni interceptae inter punctum tangentis D et punctum C ubi curvam alteram contingit. Atque ita per consequens curva tota DDC aequabitur lineae BA et DA. Et cum in circulo ut notum est, punctum D sit dimidium lineae AB, erit haec curva integra DDC aequalis radio AB una cum media parte ejusdem radij. Et ita data curva geometrica, curva ex reflexorum radiorum intersectionibus orta tam integra quam quoad omnes partes semper erit mensurabilis. Emblemata a multis excogitata in honorem Regis vestri, qui singularibus suis factis se toti mundo admirabilem praestat, allusione facta ad solem, quem sibi pro symbolo elegit, et hinc meo judicio ex data tam singulari proprietate solis, curvas in rectas transmutante, non inconcinne emblema formari posset. Sed ut in proposito progrediar inveni etiam circuli BAC esse ad spatium curvâ DDC et lineis BC, BD comprehensum ut 4 ad 3. Quodque haec curva DDC tunc admodum expedite per puncta possit designariGa naar voetnoot4). Sed haec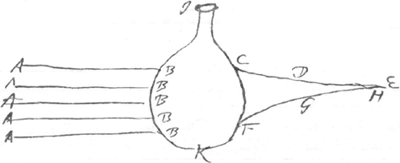 | |
[pagina 382]
| |
non tanti momenti sunt, cum facile jam infinita ejusmodi particularia reperire. Pergam igitur ad inventa quae generaliora sunt. Hisce jam mihi notis circa reflexionem, mentem converti ad refractionem, et observavi radios solis repraesentatos per omnes AB ita refringi per vitrum aqua repletum IK ut quoque harum intersectiones curvas designent CDE, FGH. Est autem valde curiosum et nescio an ab alijs observatum curvas hasce CDE et FGH naturales iridis colores exhibere, quae, si his supponatur aqua calida multum exhalans, ipsis oculis clarissime cernuntur, aut etiam pulvere radijs hisce insperso. Possem hic similia Theoremata at non minoris momenti ut antea circa reflexionem offerre, sed qui superiora novit, haec utique quoque in potestate habet eruendi. Cum autem ad similes curvas determinandas inprimis calculo tangentium opus sit, et dum in eis determinandis occupatus essem, occurrit mihi methodus tangentes ducendi generalis, tum ad curvas geometricas, tum ad mechanicas sese extendens, et adeo expedita ut existimem faciliorem non posse dari. Sit curva geometrica BDEGa naar voetnoot5), cujus natura, ut fieri solet, calculo expressa sit (BC supponatur ∞ x, CD ∞ y, AB ∞ t).  1. Termini aequationis ita disponantur ut potestas maxima y quae dari potest sola sit ab altera aequationis parte (e. gr. yy ∞ 2ax - xx) vel si ea desit ponantur omnes aequationis termini ∞ o (sic xy ∞ aa redigitur ad xy - aa ∞ o). 2. Fiat fractio cujus denominator hoc pacto constituatur. Omnibus terminis ubi cognitae (adhaerentes indeterminatis x et y) unius sunt dimensionis praefigatur unitas, ubi duarum dimensionum binarius ubi trium dimensionum, ternarius, atque ita porroGa naar voetnoot6). 3. Numerator vero, ita construatur. Omnibus terminis ubi x unius dimensionis praefigatur unitas, ubi duarum binarius, ubi trium ternarius; ablata vero ab omnibus hisce terminis x, unica dimensione; Eritque fractio ejusmodi aequalis tGa naar voetnoot7). Jam eadem ratione hinc facile similes regulae eliciuntur, licet non tam simplices ad determinandas lineas AC, CF, DF, AD &c. Ex gr. ad determinandam lineam AC, fiat fractio ut antea per easdem leges, et numeratori adjungantur omnes termini ubi x unius dimensionis, praefixa unitate; ubi x duarum dimensionum praefixo binario, ubi trium ternario, atque sic porro, eritque fractio talis aequalis AC. | |
[pagina 383]
| |
Quantum jam attinet ad mechanicas, notandum me nullum discrimen videre inter eas quas Cartesius geometricas appellat et mechanicas, quas a geometria excludit, nisi quod in geometricis curvis x et y exprimantur per rectas lineas, et in mechanicis x et y curvarum portiones designent, quae cur a geometria ideo excludendae sint, nullo modo percipio. Atque sic ego concipio eandem curvam ex gr. yy ∞ 2ax - xx (a Cartesio geometricam dictam) semper mihi infinitas curvas designare et omnium harum infinitarum curvarum tangentem una
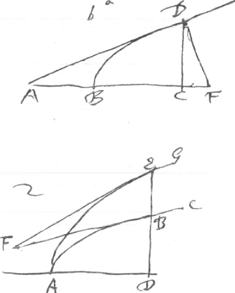 et eadem opera ope datae regulae determino; sit ex. gr. curva quaevis ABC (fig. 2) ejusque portio AB aequalis x et BE ∞ y. Eadem natura yy ∞ 2ax - xx mihi infinitas curvas repraesentat, prout loco ABC alia ac alia curva substituitur. Harum vero infinitarum tangentes sic determino. Est enim (juxta regulam modo exhibitam in fig. 1) linea AB ∞ 2ax / 2a - 2x sive ax / a - x et hinc AC juxta ea quae subjunxi ∞ 2ax - xx / a - x. Jam in fig. 2 fiat FB tangens curvam ABC ∞ 2ax - xx / a - x, linea ducta FE tanget curvam AEG, qualiscumque curva ABC etiam sit. Atque ita tanta universalitate et expedita admodum ratione infinitarum curvarum tangentes una et eadem opera exhibentur. Sed harum rerum plura aliquando communicare licebitGa naar voetnoot8). Possem hinc regulam deducere ad maxima et minima determinanda admodum simplicemGa naar voetnoot9); haec enim nihil aliud sunt quam speciales tangentium casus et per consequens determinari debent regula adhuc simpliciori quam est ea quae tangentes docet invenire. Possem innumeras hinc quadraturas magna dexteritate exhibere; sed ijs qui sciunt quod tangentes determinare et quadraturas exhibere unum et idem sit haec facile constabit. Quanquam methodum pro quadrandis curvis quantitatibus peculiarem etiam habeam, ubi nullatenus tangentes considerandae, et qua omnes possibiles quadraturae tam simplici ratione derivantur, ac hactenus nullibi simile quid observavi | |
[pagina 384]
| |
ab alijs editumGa naar voetnoot10). Nec dubitabit Vir Nobilissimus (utpote harum tam gnarus ac ullum fere offendi) quod jactis similibus fundamentis, praeclara multa deducere possem. Sed hac vice hic sistam, enixe rogans ut haec qualiacunque specimina mearum inventionum aeque favorabiliter respicere velit, ac specimina methodi qua quotcunque intermedios terminos aequationum aufero, et hinc omnium aequationum radices universaliter determinoGa naar voetnoot11) (quae ante duos annos communicavi) dignatus est recipere: Quodque tibi certo persuadeat me ex integro esse
Illustrissimi Viri
ad quaevis officia praestanda humillimum servum Ehrenfried Walther de Tschirnhaus Eques Lusatiae Superioris. |
|


