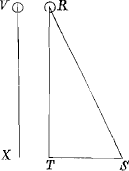
Scholium.
Ex his omnibus manifestum est quod si corpus R in linea curva moveatur cujus particula sit RS data temporis particula quam minima descripta, sitque hujus resistentia directa ut quadrata velocitatis atque adeo ut RSquad.; erit resistentia obliqua secundum plagam RT ut RS × RT et resistentia obliqua secundum plagam TS ut RS × TS. Et propterea si corpus R urgente gravitate et resistente aere descendat sitque RT horizonti perpendicularis et TS horizonti parallela, et corpus R, ob resistentiam tandem gravitate fere aequalem factam, accelerari adeo desinat utGa naar eindc) longitudo RS pro data habere possit; resistantia horizontalis (id est quae fit secundum plagam lineae TS) erit ut longitudo TS, hoc est ut velocitas horizontalis corporis R; ideoque datur curvae descriptae asymptotos horizonti perpendicalis quam corpus R (per corol. Prop. I lib. 2. Princip. Math.) nunquam transgredieturGa naar voetnoot5).Ga naar einda)
|
-
voetnoot1)
- Nous avons pu retrouver les pièces Nos. 2540, 2541 et 2542 et 2543 grâce à l'excellent catalogue de manuscrits de la Bibliothèque royale de Hannover publié par M. Bodemann sous le titre:
Der Briefwechsel des Gottfried Wilhelm Leibniz in der Königlichen öffentlichen Bibliothek zu Hannover. Beschrieben von Dr. Eduard Bodemann, Königl. Rath u. Bibliothekar zu Hannover. Hahnsche Buchhandlung. 1889. in-8o.
Il est souvent fait mention de ces pièces dans la correspondance de Leibniz et Jean Bernoulli, à laquelle nous empruntons les passages suivants, que l'on retrouvera facilement dans l'ouvrage de Gerhardt (Lettre No. 1914, note 12), d'après la publication intitulée:
Virorum Celeberr. Got. Gul. Leibnitii et Johan. Bernoullii Commercium Philosophicum et Mathematicum Tomus Primus ab anno 1694. ad annum 1699. (Tomus Secundus, Ab anno 1700. ad Annum 1716.) Lausannae & Genevae, Sumpt. Marci-Michaelis Bousquet & Socior. mdccxlv. 2 Vol. in-4o.
Aux pages 155, 159, 166, 171, 177, 184, 203 du Tome I il est fréquemment question de notes marginales inscrites par Christiaan Huygens dans l'exemplaire des Acta Eruditorum qui lui avait appartenu et dont la découverte fut annoncée par J. Bernoulli à Leibniz dans une lettre du 7 avril 1696 en ces termes:
‘Nuper Novi nostri Gubernatoris Principis Nassovii Informator mihi misit Actorum Lips. annos 1690, 1693 & 1694, quos coëmit in auctione Librorum Hugenii; invenio ibi varias notas criticas breves quas Hugenius ad marginem plumbagine scripsit & plerasque super ea, quae Tu, Dominus Tschirnhaus, Frater & ego publicavimus; nec Tibi, nec nobis pepercit, praesertim Fratris multa ipsi displicent; si curiosus es, ea quae Te concernunt Tibi transcribam. Curabo ut etiam caeteris annis potiar, ut quid de aliis senserit videam’. (Page 155, Tome I).
Quoique l'exemplaire des Acta sur lequel Huygens a écrit ces notes ait échappé jusqu'ici à nos recherches, les copies de ces notes, telles qu'elles ont été transmises à Leibniz, ont été retrouvées et copiées sur l'original par M.D.J. Korteweg. Nous les publierons dans la suite.
A l'occasion d'une note relative à la démonstration que Leibniz avait donnée de la ligne isochrone, Bernoulli écrit à Leibniz, le 27 octobre 1696:
‘Non est cur Te moveat Hugenii festinatum judicium, non enim statim emendanda sunt, quae ipsi displicuerunt; ipse potius multa multis in locis habet, quae correctionem admitterent. Nuper hac transiens Wismariensis quidam promisit, se mihi missurum aliquod manuscriptum Hugenii, in auctione ipsius librorum coëmptum, cum Newtoni Tractatu, cui Manuscripto titulus esset Newtoni Errores; quod si obtinuero, Tibi si illud desideras, transcribi curabo, aut si nimis fuerit prolixum, principaliora mittam excerpta’ (Page 208, T. I).
Leibniz répond en novembre:
‘Gratissimae erunt censurae Hugenii in Opus Newtoni, rogoque, ut si observare potes, totum mihi cures describi. Et hos & caeteros pro me sumtus reddam lubens merito’ (Page 211, T. I).
En janvier 1697, Bernouilli revint à ce sujet en écrivant à Leibniz:
‘Cum Groningius ad Te scripserit, nihilne attigit de Manuscriptis Hugenianis mihi promissis.’ (Page 232, T. I).
Ce Groningius (Johann Groening, voir la note 2) était en effet le ‘Wismariensis quidam’ de la lettre du 27 octobre 1696.
Leibniz répond le même mois:
‘Dominus Groningius nihil vel de Te, vel de Manuseriptis Hugenianis; unde ego quoque dissimulavi talia mihi ex Te esse nota, quae ipse attingere noluerat. Praesertim cum se se novam Newtoniani operis editionem moliri scripserit: quam tamen dissuasi, quod de ea cogitare Newtonum ipsum intellexissem. Et suspicor Hugeniana ibi adjicere voluisse. Quod si iterum scribat, videbo an commode efficere possim ut haec nobis communicet, praesertim si editionis cogitationem deposuerit.’ (Page 241, T. I).
Il paraît que Groening n'a pas voulu se dessaisir des manuscrits hugeniens avant de les avoir publiés. Au moins, il n'en est plus question entre Leibniz et Bernoulli avant décembre 1713, lorsque Bernoulli, répondant à une communication de Leibniz d'après laquelle Huygens aurait noté dans son exemplaire des Principia plusieurs erreurs de Newton, écrit:
‘Errores illi, quos dicis Hugenium ad marginem Exemplaris sui in Newtono notasse, sunt forte non alii, quam qui jamdudum extant ad calcem Historiae Cycloïdis a quodam Groningio Wismariensi editae; forte etiam ab ipso Groningio Tibi hoc narratum fuit, nam et mihi narravit cum ex Batavis veniens Groningae transiret, & in transitu gradum Doctoratus Juris capesceret, sed nihil eorum omnium, quae ego notavi in Newtono, ab Hugenio notatum fuit; Et certe haud valde magni momenti sunt notae Hugenianae, possetque Newtonus gloriari, si caetera omnia in Opere suo recte se haberent’ (p. 328, T. II).
Les documents, par lesquels Groening a tâché de donner quelque relief à son Historia Cycloeïdes (voir la note suivante) out été envoyés à Leibniz avec une lettre de Groening du 7 avril 1701, dans laquelle il dit: ‘Aliqua ex Hugenii annotatis Historiae Cycloeidis adjeci. Mitto autem autographum ut videas ipsemet quid et quale sit. Sed et alia erant si recte memini quae quondam in Hollandia accepi, nunc vero plura invenire haud potui. Credo Wismariae inter mea latere.’ Dans le Catalogue cité de M. Bodemann ils se trouvent décrits, sous le nom de Newton, comme il suit: a. eine Abhandl. Newtons, betr. die Gesetze der Bewegung, Anfang: Definitio, Resistentiam voco vim omnem, qua motus corporis retardatur, eamque directam et absolutam nomino quae motui directe opponitur, obliquam quae oblique (1 Bog. fol.); darauf oben links von Huygens' Hand bemerkt: R (=Reçu?) de Mr. Newton à Londres...Aug. 1689. (C'est notre No. 2540). Dabei eine Anlage von Huygens mit der Überschr. ad propos. Newtoni (notre No. 2542). b. Noch ein Concept Newtons über dens. Gegenstand (½ Bog. fol.) (notre No. 2541). c, a. Conjecturae de sphalmatis typographicis in Newtoni philosophiae principiis mathematicis von Huygens' Hand (1 Bog. fol.) c, β Alia errata ex Newtoni mei codice Londini 13. Mart. 1889/90 von Huygens' Hand (½ Bog. 4o); (ces deux pièces trouveront leur place dans la correspondance de 1691, parce qu'elles furent envoyées par
Huygens à Fatio de Duillier le 18 décembre de cette année); darin noch 1 Blatt mit der Übersch. ad propos. lib. 2 p. 334 (näml. der N'schen Principia philosophiae); cette dernière pièce, de même nature que le No. 2542, forme notre No. 2543.
-
voetnoot2)
- Johann Groening, docteur en droits, avocat et référendaire du tribunal royal de Wismar, fut l'auteur de plusieurs ouvrages de jurisprudence et d'histoire. Il publia les notes manuscrites trouvées dans l'exemplaire des Principia de Newton, qu'il avait acheté à la vente de la bibliothèque de Huygens. Elles sont insérées dans son écrit:
Johannis Groningii D. Historia Cycloeidis Qua Genesis & Proprietates Lineae Cycloeidalis praecipuae, secundum Ejus Infantiam, Adolescentiam & Juventutem, Ordine chronologico recensentur. Nec non An Primus Ejusdem Inventor, Galilaeus et Demonstrator Torricellius fuerint, contra Pascalium aliosque Galliae Geometras discutitur Perscripta Ad Illustrem & Celeber. Polyhistorem Dn. Antonium Magliabecchium, Sereniss. Cosmi III. Magni Etruriae Ducis Bibliothecae Praefectum. Accedunt Christiani Hugenii Annotata Posthuma In Isaaci Newtonii Philosophiae Naturalis Principia Mathematica. Hamburgi, Ap. Gotfr. Liebezeit 1701.
Dans l'exemplaire de la bibliothèque de l'Université d'Utrecht, le seul que nous ayons pu nous procurer, ce traité se trouve réuni avec quelques autres dans un même volume sous le titre général:
Johannis Gröningii JC. Bibliotheca Universalis seu Codex Operum Variorum qualia sunt I. Diss. de naevis Juris Romani. II. Bibliotheca Juris Gentium. III. Historia Juris Principum: &c. IV. Historia Expeditionis Russicae Caroli XII. Svec. Reg. V. Historia Expeditionis Brittannicae ex Numismate Brandenburgico. VI. Historia Cycloeidis, contra Pascalium, Mathematicum Gallum. Dicata Augustae Memoriae Sereniss. Elect. & Principum Brunsvico-Lunebergens. Perictiones ap Stob. Sapientia circa omnia in universum quae sunt, est occupata. Ita enim Sapientia se habet circa omnia entia, ut visus circa omnia visibilia, & auditus circa omnia audibilia. Hamburgi, Sumptibus Gotfr. Liebzeitk. 1701.
L'insertion des notes à la fin de la Historia Cycloeidis a été saite sans aucune critique et même sans discernement. L'auteur les a placées les unes à la suite des autres en les attribuant toutes à Huygens, quoique les premières soient incontestablement de Newton et écrites de la main de Newton, très différente de celle de Huygens.
-
voetnoot3)
- Très probablement, cette pièce a été composée par Newton à la suite d'un entretien avec Huygens, qui avait roulé sur le mouvement curviligne des corps graves dans un milieu résistant et en particulier sur la question de savoir, si la trajectoire décrite par un corps projeté sous l'influence de la gravité et d'une résistance proportionelle au carré de la vitesse possède une asymptote verticale, oui ou non. A cette question Newton avait donné une réponse affirmative dans le ‘Scholium’ de la Prop. X du livre II des Principia (p. 269 de l'édition originale); toutesois, le raisonnement dont il s'était servi à cette occasion était très indirect, et propre à laisser subsister des doutes. (Consultez à ce sujet la lettre de Huygens à Fatio de Duillier du 7 février 1690).
-
voetnoot4)
- Voir la premiére édition des ‘Principia’, p. 13.
-
eindb)
- nego hoc [Chr. Huygens]Ga naar voetnoot6).
-
voetnoot6)
- Consultez la note 4 de la pièce No. 2542. Huygens suppose évidemment que Newton considère cC comme la résistance qu'éprouve le corps A lorsqu'il se meut effectivement suivant AC; Newton, au contraire, veut dire que cC est la résistance ‘secundum plagam oblique oppositam’, c'est-à-dire la composante selon la direction CA de la résistance ‘directe opposita’ Bb.
-
eindc)
- imo ego talem celeritatem deorsum pono, quae sentiat resistentiam gravitati aequalem ut proinde nulla sit acceleratio deorsum et quia contingit retardatio in laterali motu, hinc sequitur retardatio in motu obliquo seu absoluto [Chr. Huygens].
-
voetnoot5)
- On remarquera que ce raisonnement très juste s'applique également à tous les cas où la vitesse V et la résistance R finissent par s'approcher indéfiniment de limites finies Vo et Ro. Il est facile, d'ailleurs, de le mettre sous une forme plus rigoureuse. En effet, soient α et β deux nombres constants peu différents de l'unité et tels que, à commencer d'un moment donné, on ait toujours
V < αVo; R > βRo
et en conséquence
R > β/α V/Vo Ro.
Si alors Vx et Rx représentent les composantes horizontales de la vitesse et de la résistance, on aura
Rx = R sin ϕ > β/α Ro/Vo V sin ϕ;
c'est-à-dire
Rx > β/α Ro/Vo Vx.
Mais, dans tous les cas où la résistance horizontale serait proportionelle à la vitesse horizontale et égale à β/α Ro/Vo Vx, on sait qu'un point limite existe qui ne peut être franchi par la projection horizontale du projectile. Il est donc facile de voir que, dans le cas qui nous occupe, où des résistances supérieures correspondent aux mêmes vitesses, un tel point doit se présenter à plus forte raison et que, en conséquence, la trajectoire elle-même possèdera une asymptote verticale.
-
einda)
- R. de Mr. Newton à Londres aug. 1689 [Chr. Huygens].
|