Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2486.
E.W. von Tschirnhaus à D. Makreel.
23 août 1687.
Appendice au No. 2485.

La pièce se trouve à Leiden, coll. Huygens¹⁾.

^a) Amice Clarissime.

Absens fui a meis aedibus ultra 4 septimanas in Silesia. &c. unde facile colliges mihi satis paucum tempus reliquum fuisse, quo vestras litteras, quae ante 4 dies mihi redditae (licet primae harum ante 3 septimanas hic receptae fuerint) ut decet bene expenderem; adeoque quantum per hoc breve tempus mihi licuit assequi; hac ratione responsum generale do: ultra modum D. Voldero obligatus sum, nam hic perfectè non solum meum errorem detexit²⁾ sed et aliqua ex parte unde meus lapsus originem traxerit; quodque sensum D. Fatii non recte fuerim assecutus optime perspexit.

Quoad primum, certum est me errasse; quod hac ratione ipse demonstro. Sint in praesenti figura quatuor fila curvae describendae, DA, AG, AG, CA. Jam sint

1) Elle est écrite de la main de D. Makreel.

a) Ad P. Gentium. ℞ 12 Sept. 1687. [Chr. Huygens].

2) Voir la Lettre N^o. 2475.

[p. 216]

sinus CT, DW, ab una parte perpendicularis AE ad tangentem aequales sinui duplae VG. ab altera parte ejusdem perpendicularis, prout vult D. Fatio, quod



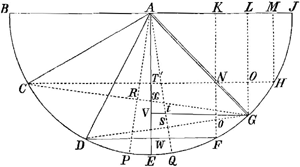a D. Voldero juxta ejus mentem optime demonstratum (sed fateor ex ejus objectione contra me nullo modo tale quid suspicari potuissem et nescio num ullus alius nisi cui haec ipse indicavit) hoc posito clarum est sinus hos CT, VG, DW, vel quod idem sinus TH, VG, WF progressionem servare arithmeticam; ac proinde excessus horum aequales esse hoc est: NO aequari OH; Ponamus jam juxta me, angulos DAG, CAG & PAQ bifariam divisos esse per rectas AS, AR, AE: Jam clarum, angulum RAX five PAE aequari angulo XGV (propter communem X & rectos R & V, in triangulo RAX, VGX) hoc est TCX sive HCG (propter parallelas CH et VG) porro patet ob easdem rationes Angulum VAt sive EAQ aequari angulo SGt (propter communem t et rectos V et S in triangulis AVt et GSt) hoc est angulo SDW, sive GDF (propter paralllelas VG & DW) cum itaque angulus PAE aequatur angulo HCG, item angulus EAQ aequatur angulo GDF juxta me Angulus PAE aequalis angulo EAQ; patet angulum HCG aequari angulo GDF, et per consequens arcus HG aequatur arcui FG; quod apertè falsum est, si ut modo ostensum NO aequalis OH, nam hinc quoque OG & oF deberent aequales esse; Clarissimum itaque est me in fig. 19 pag. 74 mei Tractatus³⁾ errasse verum omnia reliqua in Articulo tertio de Tangentibus vera sunt de quo statim. Quoad secundum: optimè quoque D. Volderus caussam Erroris perspexit, quod ego angulum bifariam esse dividendum dixerim, cum tamen hoc de certa linea recta ipsi angulo subducta intelligendum est; sed dixi aliqua ex parte hoc D. Volderum perspexisse nam ego insuper duas ejusdem rei sed diversas ab hac vias id ipsum certo determinandi quoque excogitaveram et quae mihi videbantur eandem conclusionem formare. Hoc itaque maximè me decepit, quod triplici diversa via idem videbar mihi colligere; et quod magis. quod haec quoad sensum cum praxi perfectissime videbantur consentire; prout quilibet qui haec tentare velit perspiciet. Quod fateor mihi in vita unquam contigisse non memini.

3) Voir la pièce N^o. 2461.

[p. 217]

Quoad tertium ubique sensum in objectione D. Fatii nullatenus percepi; sed nec potui, nam certum est quod ille me nullius erroris suo ratiocinio convicerit: quod modo non putabitis me ex passione jam loqui, cum errorem meum libere confessus sum, id quod sic ostendo. Primum concedo quod mentem ejus non satis universaliter expresserim dum dixi⁴⁾ quod solum Ellipsi quadrarent quae ille perhibet; sed assumamus ea quam universalissimè. Sint duo foci D. Fatii A, C, in quae infinita



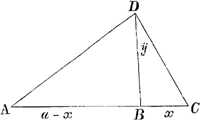fila coincidunt. Jam erit DC √xx+yy et AD √aa-2ax+xx+yy; ponamus numerum filorum AD esse b et numerum filorum DC ∞ c. Erit itaque b√aa-2ax+xx+yy + c√xx+yy ∞ d. Adeoque quicquid ille demonstrat non infinitis curvis convenit, ut putat, sed unicae curvae cujus natura modo expressa quaeque quartum gradum non transcendit haecque curva saltem infinitas species sub se habet; prout datur infinitarum Hyperbolarum et Ellipsium species pro b et c alios ac alios numeros designant: sique ponamus (quem casum ego saltem consideraveram) b et c aequari; quicunque sint numeri et proinde quaecunque fila, non nisi ellipsis provenit; eadem ratione: superiores curvae pro varia cognitarum assumptione, ad inferiores gradus quandoque reducuntur; eadem ratione. Ellipsis ad circulum quoque reducitur: cum itaque si rectè velimus loqui D. Fatio non nisi unicae curvae modo expressae, quaecunque numero sint fila, tangentem hac sua demonstratione exhibuerit; non video certe qua ratione adhuc dum ego aut quicunque alius ullum errorem circa mea (licet aliquis certo adfuerit) potuerim ex ejus objectione perspicere: Quod autem hoc de sinibus intellexerit cum expressè hoc non indicavit id nullo conjicere potui: unde porrofactum quod existimarem, regulam ejus propositam eam ipsam esse quam universalem esse pro determinandis Tangentibus nobis exhibebat; quam ut talem necessario quoque falsam debui dicere et ostendere. Quoad litteras D. Hugenii, miror ultra modum quid dicat in ultimis suis: expecto indies num quae a D. Tsch. confessio erroris adferatur, quae quam diu cessabit, putabo eum illa animi commotione....nondum quievisse⁵⁾: sane videbit hic contrarium ingeniosissimus vir, et licet vix 4 dies sint, quod has litteras acceperim ecce confessio erroris mei. Putatne quod error in mathematicis commissus mihi mentis tranquillitatem ullo modo turbare possit, parum me novit si hoc de me credat.

Certe non magis hoc me turbaret unquam, quam si aliquis mihi lapsum, in calculo arithmetico seu ordinario a me commissum ostenderet, cum Mathesis ad eandem perfectionem redacta ut nimirum aequalis ubique certè calculandi & aberrandi occasio adsit tam ingeniosissimo quam imperitissimo; adeoque hic Inge-

4) Voir la Lettre N^o. 2418, à l'article 2.

5) Voir la Lettre N^o. 2472.

[p. 218]

niosorum judicium non timeo, aliorum non aestimo. Praesertim cum licet in casu illo particulariter in fig. 19 aliquis error sit, non ideo erronea sunt reliqua quae in articulo 3^o pag. 73 ut et in fine ejusdem articuli pag. 75 dixi⁶⁾; haec enim meo judicio tam praestantia sunt, ut qui haecce rectè introspicient non satis hoc inventum existimare poterunt, nec credent quod magis ac pax est hoc extulerim; nam licet ipsam Regulam tangentes exhibendi non exposuissem, certum tamen est NB⁷⁾: quod⁸⁾ ostenderim necessario talem regulam dari^b) quae universalissima sit absolutè pro omnibus curvis (quod existimo pauci adhuc perspicient) non solum pro Geometrico, sed et omnibus Mechanicis curvis; quod haec facillima omnium regularum hactenus exhibitarum necessario esse debeat, quod nullus hactenus de tali cogitavit, et similia: deinde cum securus talem regulam certo dari, non difficile Analyseos perito, eandem detegere, cum jam Tangentes determinandi methodos universales habemus: ubi ex unaquaque tali methodo quascunque alias methodos derivare licet, modo quis laborem non subterfugere velit: adeoque non solum existentiam tam praestantis methodi ostendi, sed et quia curvarum omnium simplicissimam genesin aperui, qua ratione, via admodum simplici eadem possit obtineri; quae sane talia sunt ut licet alius quis illam regulam me ipso prius detegeret, non viderem quare non mihi tanquam primo inventori gratias ideo deberent, hocque judicium non solus habeo, sed in eadem sententia est D. Leibnitsius qui eadem mihi scribit⁹⁾.

Quod autem Clarissimus Hugenius existimat¹⁰⁾ trisectionem hic opus esse; video quod sententiam jam mutavit, nam credebat inprimis litteris hoc opus esse in sig. 19^c). Jam vero cum ex D. Volderi demonstratione revera observavit, verum esse quod non nisi bisectione (prout ego quoque statui) opus sit; ad alios casus hoc adstringit. Sed certè crede mihi, nil nisi bisectione vel verius constructione per solas rectas; cum Tangentes determinare, sed simplicissimum problema quod D. Fatio optimè quoque perspexit, prout in responsione meae ad D. Fatio, clarissime id demonstravi. Quod a nullo credo unquam refutabitur. Quod autem D. Fatio mihi quoque falsam Regulam affinxerit extra omne dubium est; nam licet ut D. Hugenius dicit in fig. 19. Juxta meam erroneam constructionem Arcus FL ad LG sit ut 3 ad 1. ac proinde in reciproca ratione filorum non poterat inde (quod casu se ita habet) D. Fatio colligere, meam regulam universalem (quam nondum pu-

6) Voir la pièce N^o. 2461. 2^e extrait.

7) Nous supposons que ce N.B. a été intercalé par Makreel.

8) Les mots en italiques ont été soulignés par Chr. Huygens, pour marquer les passages auxquels se rapportent ses notes marginales^b),^c),^d).

b) non video [Chr. Huygens].

c) imo de fig. 8 ibi hoc tantum affirmavi tam in priore epistola quam in secunda [Chr. Huygens].

d) non poteras sine trisectione [Chr. Huygens].

b) non video [Chr. Huygens].

9) Consultez, sur cette lettre de Leibniz à von Tschirnhaus, qui ne paraît par avoir été conservée et qui contenait des remarques sur la ‘Medicina Mentis’, un passage de la lettre de Leibniz à Huygens du 13 octobre 1690. On y verra que Leibniz avait reconnu, lui aussi, la fausseté de la règle de von Tschirnhaus et n'avait pas manqué d'en avertir l'auteur.

10) Voir les Lettres Nos. 2470 et 2472.

c) imo de fig. 8 ibi hoc tantum affirmavi tam in priore epistola quam in secunda [Chr. Huygens].

[p. 219]

blicaveram) se ita habere, ut semper arcus in reciproca ratione filorum esset secandus nam contrarium expresse dixeram, Regulam illam niti continua bisectione: nam ego ex. gr. in fig. 8, Trium filorum aliud punctum inveniebam^d). Juxta constructionem fig. 19 deinde itidem aliorum trium filorum aliud punctum juxta eandem construi deinde hunc ac inter haec duo puncta denuo bisecabam, pro determinanda tangente, atque sic in infinitum: Quid autem jam statuam brevi rescies, nam brevi vobis responsionem ad objectionem D. Fatii transmittam quae forte non solum authori sed omnibus Eruditis placebit, sed quia tot negotia jam mihi incumbunt, ut si ad ea cogitem exhorrescam, non credo quod citius poterit fieri, quam elapsis 6 aut 7 septimanis: Rogo itaque omnes amicos, quod haec considerent, et eousque cum patientia exspectent, conabur enim quantum in me omnibus satisfacere; eamque responsioneni, priusquam ea imprimatur censurae D. Hugenii, Volderi, & vobis subjiciam; hocque ultimum et primum erit quod D. de la Crosse¹¹⁾ imprimendum permittam, cum ejusmodi enim viris, qui tam incivili ratione agunt, nullum commercium stabilire unquam cogito¹²⁾ Quod dixerim quod Tractatus meus jejune admodum ab ipso habitus et permulta a meo sensu aliena celata; hoc non solum a me sed a multis aliis ita judicatum, nec mea refert, sed ad ipsum potius spectat, cum tractatus meus aliis satis notus sit: adeo ut crederem ipsum mihi ideo debere obligatum esse. Liber hic ejus mihi ad manus non est alias sat multos errores recenserem; sed non opus est hisce recensendis, tempus terere. NB. Quaeso objectiones D. Fatii contra me quam cito possibile mihi transmittas &c. Quaeso quae supra scripsi D. Hugenio & Voldero insinuare non desines, quibus ipse responsum fecissem, si temporis angustia hoc permitteret, meque amare pergas¹⁴⁾.

Kiesling 23 Augusti a^o. 1687.

Tschirnhaus.

Heri Asbestum incombustibilem hactenus exeditum lapidem, speculo meo usterio in vitrum transmutavi¹³⁾.

d) non poteras sine trisectione [Chr. Huygens].

11) Johannes Grossius, l'un des éditeurs des Acta Eruditorum. Il mourut en 1692.

12) Nous ignorons la cause de cette sortie contre Grossius, à moins qu'il ne faille la chercher dans le silence gardé dans les ‘Acta Eruditorum’ au sujet de la ‘Medicina Mentis’. Consultez la Lettre N^o. 2475, note 2.

14) Cette pièce est la dernière que nous publions au sujet de la polémique entre Fatio et von Tschirnhaus. Huygens n'y a plus pris part. Ceux qui voudront connaître la réponse de von Tschirnhaus à la pièce N^o. 2460, telle qu'il la fit paraître enfin en septembre 1688, et la réplique de Fatio du mois d'avril 1689, pourront les trouver dans la Bibliothèque Universelle et Historique, aux Tomes X, p. 497 et XIII, p. 46. De l'article de von Tschirnhaus, qui a paru sous le titre:
Réponse de M. de T. aux Réflexions de M. de Fatio de Duillier, sur sa méthode de trouver les tangentes des lignes courbes, publiée dans son Traité de la Medecine, de l'Esprit & du Corps communiquée par l'Auteur,
nous ne citerons encore que le suivant, qui se rapporte à la correspondance qui précède et dans lequel von Tschirnhaus mentionne sa lettre à Huygens du 12 mai 1687, notre N^o. 2457:
‘On doit donc savoir qu'avant que M. Fatio publiàt ses Réftexions, je savois que j'avois commis ici quelque erreur, quoique je ne visses pas encore en quoi elle consistoit. Monsieur Huygens m'aiant demandé pourquoi je n'avois publié que quelques cas pour la détermination des tangentes, & non la Regle entière, je lui repondit ainsi, avant que je susses rien de l'écrit de M. Fatio:
Cela enfin est arrivé en partie (ce que je vous dêcouvre avec confiance comme à un Ami sincère) parce que pendant que j'étois occupê à revoir le tout, autant que mes affaires le pouvoient permettre, pour l'envoier & le donner au public, je soupçonnai que je pouvois m'être trompé en quelque chose, & c'est pourquoi je ne voulus pas produire tout le Theorème, mais seulement jusqu' à l'endroit où il me sembloit que je n'avais commis aucune erreur. Je me réservai d'examiner cela en un autre temps avec application; car vous savez qu'il y a quelquefois des Censeurs rigoureux, qui ne considerent point que de semblables choses demandent un esprit fort attentif (pour cela il faut avoir du temps, ce qui m'arrive rarement) & que l'Auteur d'un Theorême peut aisément corriger de semblables bévuës &c.’
Ajoutons que dans la seconde édition de la ‘Medecina Mentis’ (voir la Lettre N^o. 2466, note 1) la construction de la figure 19 de la pièce N^o. 2461 se trouve remplacée par une autre, conforme à la règle de Fatio. Sur cette correction l'auteur s'exprime comme il suit:
‘Hic autem notandum est, circa figuram hanc 19. errorem aliquem in primam editionem irrepsisse, quem animadvertens ingeniosissimus & in hisce studiis apprimè versatus Dominus Fatio de Duilliers eundemque corrigens in egregiam & universalem incidit regulam, ope centri gravitatis simile quid praestandi, quâ de re, si ita placet videri ea possunt, quae ejus causâ nos inter acta fuerunt, insertaque tractatui, qui inscribitur Bibliothèque Universelle Ann. 1687. Tom. 5. pag. 25. Quia autem, dum in demonstrationem alicujus theorematis inquiriimus, circa figuras Mathematicas occupati non facile ad pondera & gravitatem respicimus, inde factum est ut nullatenus tale quid hîc subesse suspicarer, sed per laudatum illum virum admonitus attentè rem considerando illicè demonstrationem hanc detexi, credidique eam ipsam procul dubio esse, in quam iste incidisset. Ast ex ultimâ ejus responsione percepi, demonstrationem meam multò adhuc esse faciliorem, ac quae ab Eodem publicata extat, prout suo loco ostendam.’
Voulant ensuite renchérir sur Fatio, von Tschirnhaus expose une méthode des Tangentes qui s'appliquerait au cas plus général de courbes dans lesquelles, au lieu de la somme des rayons vecteurs partant de quelques foyers, la somme de leurs n-ièmes puissances serait constante. Malheureusement sa méthode, exacte, quoique moins élégante que celle de Fatio, pour le cas n=1, ne l'est plus pour d'autres valeurs de n, à moins que les foyers ne soient situés sur une même droite et que la transversale sur laquelle von Tschirnhaus mesure ses grandeurs f, g etc. ne soit parallèle à cette droite. Fatio, au contraire, avait donné dans sa réplique, citée plus haut, deux constructions différentes, l'une et l'autre élégantes et valables pour toute valeur de n et pour une situation quelconque des foyers.

13) Voir la Lettre N^o. 2444.

b) non video [Chr. Huygens].

c) imo de fig. 8 ibi hoc tantum affirmavi tam in priore epistola quam in secunda [Chr. Huygens].

d) non poteras sine trisectione [Chr. Huygens].