Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 159]

N^o 2461.
E.W. von Tschirnhaus.
1687.
Appendice II au No. 2459.

Extrait de la Medicina Mentis.

(1^e Extrait p. 68, 69).

Assumantur puncta in 5. fig. unicum A. in 6. fig. duo A & B. in 7. fig. tria CAB. in 8. fig. quatuor C, A, B & D &c. sive in eâdem recta existant sive non; sive aequali

Fig. 5

Fig. 6

Fig. 7

distent intervallo sive inaequali, perinde est. Assumatur jam in 5 fig. filum A B, alligatum in A, & continuetur in B; in 6. fig. filum alligatum in A, per C continuetur in B, ubi denuò alligetur; in 7. fig. filum in A alligatum continuetur in D, dehinc in B, postea rursus in D, & iterum dehinc in C, ubi etiam alligetur; in 8. fig. continuetur ex A per E.B.E.C.E. usque in D, atque ita in insinitum: concipiantur jam stylo quopiam in 5. fig. in B; in 6. fig. in C; in 7. fig. in D, ac in 8. fig. in E. &c. omnia fila aequaliter in rectas extendi & ita incoepto styli motu, eoque continuato, quo usque fieri potest, curvae BCD, CDE,

[p. 160]

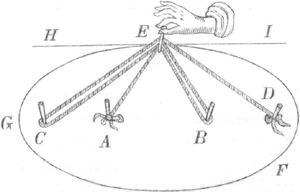Fig. 8

DEF, EFG &c. delineantur. Hinc jam facilè patet, semper in posterioribus contineri, quae in prioribus. Si enim in fig. 8. supponamus duo puncta coincidere, curva 7. fig. describetur, & si in 7. fig. rursus duo puncta coincidant, curva 6. fig. describetur; si vero in hac fig. duo quoque concidant puncta, circulus delineabitur.

(2^e Extrait p. 73-75).

Tangentes statim ex ipsâ descriptione, sine ullius calculi ad eas inveniendas usu, determinari. Quâ de re haec pauca praecipere placet. Sit 1. descripta curva,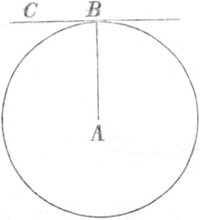

Fig. 14

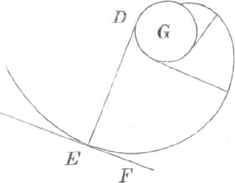Fig. 15

quae unicum habeat centrum: hoc sive sit punctum A, uti in fig. 14. sivè quaecunque curva G in fig. 15. Si jam ad extremitates radiorum, AB in 14. fig. & DE in 15. fig. has curvas describentium, erigantur perpendiculares BC & EF, hae curvas descriptas tangent. Sint 2 curvae ex duobus centris descriptae, sive haec centra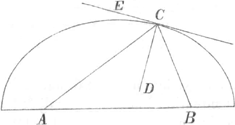

Fig. 16

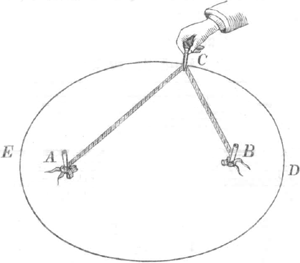
sint puncta, uti in fig. 16. sive quaeçunque curvae, veluti in fig. 17. sive tandem curva quaecunque & punctum, quod fig. 18. exprimitur: si angulo ACB bifariam per lineam CD diviso, tunc excitetur perpendicularis CE, haec curvam hâc ratione discriptam in C tanget. Sint 3. in fig. 19 tria centra B, C, D, seu sint sola puncta, seu solae curvae, seu quaevis curvae, quae

[p. 161]

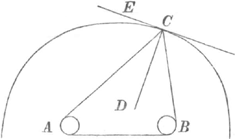Fig. 17

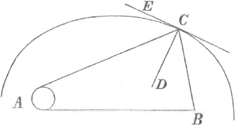Fig. 18

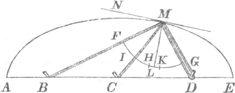Fig. 19

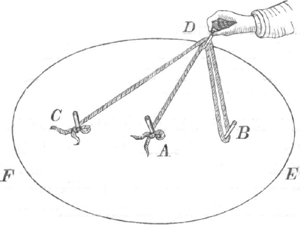
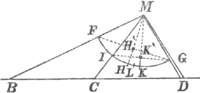
omnibus modis, pro nostro arbitrio, situm variant. Dividatur arćus FG extremorum filorum BM & DM bifariam in H. Dein arcus IG, interceptus inter filum intermedium CM & filum duplicatum DM in K. Denique arcus HK denuò bifariam in L. Ducatur tunc LM, & huic in extremitate M statuatur perpendicularis MN; haec curvam AME in puncto M. tanget¹⁾. Atque ita possem progredi, ostendendo ope ejusmodi continuae bisectionis constanti ratione in infinitum ad regulam ordinatae millium millionum curvarum tangentes exhiberi. Dabiturne per totam mathesin universalius, aliudve utilius theorema, aut praestantior tangentes determinandi methodus? Quis crederet eam hactenus alios latuisse, post tot diversos hâc in re conatus, postquam primum mathematicis, quantae haec sint utilitatis rectè innotuit? Sed facilia multa, ingeniosissimos etiamnum fugiunt, quae tamen permagni sunt momenti. Oportet autem ut theorematis adeo generalis demon-

1) Asin de pouvoir suivre plus sacilement la polémique qui va




s'élever sur la construction représentée dans la figure 19, il sera bon de remarquer dès l'abord en quoi elle différe de la construction exacte, décrite par Fatio dans la pièce précédente, le N^o. 2460.
D'après cette dernière construction, on doit assigner des masses égales aux points F et I et une masse double au point G (voir la figure). Pour déterminer ensuite le centre de gravité commun de ces masses, on peut commencer par composer la moitié de celle du point G avec la masse de F et l'autre moitié avec celle de I. On trouve ainsi les nouveaux centres de gravité H′ et K′, qui sont situés sur les bissectrices MH et MK des angles FMG et IMG.
Jusqu'ici les deux constructions peuvent étre considérées comme identiques en tant qu'elles mènent à la bissection des mêmes angles, mais ensuite, pour achever la construction de la normale, on doit la faire passer selon Tschirnhaus par le milieu L de l'arc HK et selon Fatio par le milien de la droite H′ K′.
D'après les pièces N^o. 2475 et N^o. 2486, c'est surtout en faisant ressortir cette différence entre les deux constructions que de Volder a réussi enfin à faire reconnaître par Tschirnhaus l'erreur qu'il avoit commise.

[p. 162]

stratio sit perquam facilis. Eam quibusdam ex parte explicui, & suo loco tradam, ubi porrò monstrabo²⁾.

2) Cette démonstration ne se trouve ni dans la ‘Medicina Mentis’ ni ailleurs. Consultez la Lettre N^o. 2457, pp. 143 et 144.