Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 154]

N^o 2460.
N. Fatio de Duillier.
mars 1687.
Appendice I au No. 2459.

La pièce a ètè imprimèc dans le Bibliothèque Universelle et Historique¹⁾.

Reflexions de Mr. N. Fatio de Duillier sur une méthode de trouver les tangentes de certaines lignes courbes, laquelle vient d'être publiée dans un Livre intitulé Medicina Mentis²⁾.

L'Auteur de la Medecine de l' Ame propose, dans son Traité³⁾, une méthode qui n'est pas entierement exacte pour trouver les tangentes de diverses lignes courbes, qui se décrivent par des fils. Sans doute il a jugé que cette méthode étoit bonne,

Fig. 1

1) Article II du numéro d'avril 1687.
Il nous a paru indispensable de reproduire ici en entier l'article de Fatio, parce qu'il en est question dans plusieurs des lettres de l'année 1687. Nous y ajoutons, pour la même raison, sous le N^o. 2461, deux extraits de la ‘Medicina mentis’.

2) Sur la part que Huygens a eue dans l'invention de la méthode exposée dans cette pièce, et à la rédaction de la pièce elle-même, consultez la Lettre N^o. 2467, note 2 et l'Appendice II, N^o. 2469.

3) Voir la pièce N^o. 2461.

[p. 155]

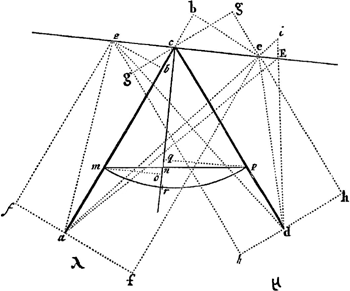
faute d'examiner assez une pensée, qui paroît vraie par induction, & qui semble dans la pratique ne s'éloigner pas beaucoup de la verité: mais qui néanmoins ne répond nullement à l'exactitude geometrique, excepté dans quelques cas particuliers, & lors que les lignes décrites par les fils sont plus simples.

Supposons que a & d, dans la premiere figure, foient les foiers d'une ligne courbe qui passe par le point c, & qui se décrive par le moien d'un sil, dont les deux extrémitez soient attachées aux foiers a & d. Je suppose ici que les extrémitez du fil sont attachées à ces foiers, afin que la ligne courbe soit du nombre de celles que Mr. de T. considere; mais autrement ce que je vai démontrer s'étend à des lignes courbes, qui se peuvent décrire par un fil, dont une extrémité est attachée au stile, & l'autre à un des foiers; & même il s'étend à des lignes courbes, qui ne se peuvent point décrire par des fils, selon la maniere de Mr. de T. à moins d'en emploier une infinité de retors. Soit λ le nombre qui exprime la multitude des fils en a c, & μ le nombre qui exprime la multitude des fils en cd. Ainsi la ligne a c multipliée par λ, plus la ligne c d multipliée par μ, est égale à toute la longueur du fil qui est donnée; & en géneral la nature de la courbe est telle, que de tout autre de ses points tirant une ligne au foier a, & une autre ligne au foier d, la premiere multipliée par λ, plus la seconde multipliée par μ, font toûjours une même somme.

Pour trouver la perpendiculaire sur la courbe au point c par exemple, je prens sur les lignes c a & c d des longeurs égales c m & c p, & aiant mené la soutendante m p je la divise au point n, de maniere que mn soit à n p reciproquement comme le nombre μ au nombre λ; & je dis que la ligne c n est la perpendiculaire demandée. La ligne c e, que je suppose perpendiculaire sur c n sera donc la tangente de la ligne courbe au point c.

En effet quelque point que l'on prenne sur c e, par exemple le point e, que je suppose d'abord placé du côté de a, il se trouve hors de la courbe, comme je le vai prouver.

Soient menées des points m & p les lignes m o, p q, perpendiculaires sur c n, & du point e la ligne e b perpendiculaire sur c a; de plus soit menée e h parallele à c d, & sur e h les perpendiculaires cg, dh; enfin soit menée e f parallele à c a, & sur ef la perpendidulaire a f.

A cause des triangles semblables c m est à o m comme e c est à c b; & c p ou c m est à p q comme e c est à e g; donc o m est à p q comme c b est à e g. Or par la construction o m est à p q comme le nombre μ au nombre λ; donc c b est à e g comme le nombre μ au nombre λ, & par conséquent λ c b est égal à μ e g; c'est à dire que la ligne c b multipliée par le nombre λ est égale à la ligne e g multipliée par le nombre μ.

λ a b, plus λ b c, plus μ c d est la longueur du sil égale à λ f e plus μ e g plus μ g h, égale encore à λ f e plus μ e h. Tirant à present du point e aux foiers a & d les lignes e a, e d, lesquelles représentent la situation qu'auroient les fils s'ils atteignoient le point e, on à λ a e plus μ e d pour la somme des fils qui atteindroient le

[p. 156]

point e, laquelle somme est plus grande que λ f e plus μ c h⁴⁾ qui est la veritable longueur du fil: ce qui marque que le point e n'est pas dans la ligne courbe proposée.

Le point e, qui est du côté de d, n'est pas non plus dans la courbe, comme il paroît par la démonstration suivante. Soit menée du point e la ligne e b perpendiculaire sur c a; de plus soit menée e h parallele à c d & sur eh les perpendiculaires c g, d h; ensin soit menée e f parallele à c a, & sur e f perpendiculaire a f.

A cause des triangles semblables, il se trouve, comme ci dessus, que λ c b est égal à μ e g. A present λ a b moins λ b c plus μ c d est la longueur du fil, égale à λ a b moins μ e g plus μ c d égale encore à λ f e plus μ e h. Mais tirant du point e aux foiers a & d les lignes e a, e d, qui représentent la situation qu'auroient les fils s'ils atteignoient le point e, la somme des fils se trouveroit être λ a e, plus μ e d, plus grande sans contredit que leur veritable somme λ fe plus μ e h. Ainsi le point e n'est pas non plus dans la ligne courbe proposée.

Il n'y a donc aucun point de cette ligne courbe, excepté c, qui tombe sur la ligne e c. J'ajoûte qu'aucun point de la courbe ne tombe, à l'égard de la ligne e c, du côté opposé à celui où se trouve le point n. Car soit i, s'il est possible, un tel point de la ligne courbe, & du point i soient tirées aux deux foiers a & d les lignes i e a, i E d, qui coupent la ligne e c dans les points c⁵⁾ & E, & soient ensuite tirées les lignes, e d & E a. Si λ est plus grand que μ, λ a e plus λ e i plus μ i d sera plus grand que λ a e plus μ e d, qui excede la longueur du fil⁶⁾ comme il a été démontré, ou qui lui est égal si le point e tombe en c: ainsi la ligne courbe ne passe pas en i. Mais si μ est plus grand que λ, μ d E, plus μ E i plus λ i a sera plus grand que μ d E, plus λ E a, qui excede la longueur du fil, ou du moins qui lui est égal; & par conséquent la ligne courbe proposée ne passe pas non plus par le point i.

La méthode de Mr. de T. se réduit à diviser l'arc m p décrit du centre c en r, de maniere que l'arc m r, soit à l'arc r p réciproquement comme le nombre des fils en c d au nombre des fils en c a;⁷⁾ & la ligne menée par les points c & r doit être, selon lui, perpendiculaire sur la courbe. Mais j'ai démontré que la veritable perpendiculaire divise la corde m p en n, suivant cette même raison reciproque: ce qui peut faire juger que la méthode de Mr. de T. approche en quelque sorte

4) Lisez: μ e h.

5) Lisez: e.

6) A la page 278 du livre F des Adversaria de Huygens on rencontre la remarque suivante, qui se rapporte évidemment à ce passage:
Ad demonstrationem Fatii in Bibliothèque universelle. 100 id + ia potest esse minor quam 100 ed + ea propter angulum obtusum i. Sed tunc 100 id + ia non potest esse minor quam 100 Ed + Ea, quae majora vel saltem aequalia ac + cd (lisez ac + 100 cd).

7) Il est vrai que von Tschirnhaus n'a pas formulé explicitement le théorème que Fatio lui attribue ici; mais la construction que Fatio indique n'est en effet qu'une conséquence logique de celle employée par Tschirnhaus dans la figure 19 de la pièce N^o. 2461. Voir là-dessus la Lettre N^o. 2468, au paragraphe N^o. 3 et l'annotation c) de Huygens.

[p. 157]

de la verité, quoi qu'elle ne s'accorde pas avec ce que j'ai démontré ci-dessus. Cela paroîtra davantage, si on la compare avec soin au théoreme suivant, duquel j'ai la démonstration⁸⁾. Je substitue ce théoreme à celui que Mr. de T. donne touchant les tangentes de toutes les lignes qui sont décrites à sa maniere; & il est certain que la construction que mon théoreme fournit, pour déterminer ces tangentes, est plus simple & plus génerale que celle de cet Auteur, outre qu'elle est exacte.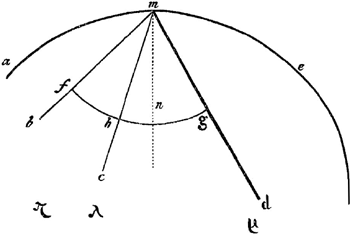

Fig. 2

Soit m, dans la deuxieme figure, un point d'une ligne courbe a m e décrite par quelque nombre de fils que ce soit, comme m b, m c, m d, attachez ou roulez autour des foiers b c d. Ces foiers peuvent être en si grand nombre que l'on voudra & dans toutes sortes de situations imaginables, sur le plan a m e.

La nature de la ligne courbe a m e est telle à l'égard de chacun de ses points, comme m, que la ligne m b multipliée par le nombre ϰ quel qu'il soit, plus la ligne m c multipliée par le nombre λ, plus la ligne m d multipliée par le nombre μ font ensemble une somme connuë.

Du centre m je décris un arc de cercle f h g, qui coupe dans les points f h g les fils m b, m c, m d, c'est à dire les lignes menées du point m aux foiers. Je suppose que dans tous ces points f h g il y ait des poids qui soient entre eux comme les

8) Voir, pour une démonstration simple et suffisamment générale de ce theorème, la pièce N^o. 2469. Cette démonstration, en effet, quoique bornée au cas de trois foyers, mais pris dans une situation quelconque, est sacilement généralisable pour un nombre quelconque de ces points, comme Fatio l'a fait d'ailleurs dans sa réplique à von Tschirnhaus (Bibliothèque Universelle et historique de l'année, 1689, Tome XIII, p. 58-61). C'est donc à tort que M. Cantor dans ses Vorlesungen über Geschichte der Mathematik, T. III, p. 149 (éd. 1898) assure, sur la foi de M. Weissenborn, que la construction de Fatio ne serait par valable dans le cas général.

[p. 158]

nombres ϰ λ & μ propres à chaque fil; & je dis que la ligne m n qui passe par le point m & par le point n, commun centre de pesanteur, de tous les poids f h g, est perpendiculaire à la courbe proposée.

Ainsi qu'elle que soit la multitude des foiers d'une courbe, comme a m e, & quels que puissent être les nombres, ou si on veut les lignes droites ϰ, λ, μ &c. (parce que les lignes droites sont plus commodes que les nombres, pour exprimer toutes sortes de proportions) le probleme de mener la tangente au point donné m de la courbe, est plan, ou plutôt d'une seule dimension & extrémement facile à résoudre.

En effet on peut démontrer, que les tangentes de toutes les lignes géometriques se trouvent par la résolution d'une égalité, ou l'inconnuë ne monte qu'à une seule dimension⁹⁾. Et je tire de là une nouvelle preuve contre la méthode de Mr. de T. Si cette méthode étoit exacte, comme la perpendiculaire sur la courbe de la premiere figure diviseroit un arc de cercle donné suivant une raison donnée, & que cependant on démontreroit d'un autre côté que cette perpendiculaire se trouve par le moien de la regle & du compas, on auroit une demonstration que le probleme de diviser un arc de cercle donné, suivant une raison donnée, seroit un des plus simples de la Géometrie, quoi que nous sachions qu'il est veritablement fort composé.

Je sai bien que M. de T. se sert, dans son Traité, d'une expression qui pourroit faire croire que sa méthode se réduit toûjours à partager quelques arcs par le milieu. Mais pour peu qu'on examine ce qu'il dit, on verra que de simples bissections d'arcs ne lui suffisent pas: ce qui paroitra fort clairement, si on suppose que le fil c a ait cinq doubles dans la premiere figure, & que le fil c d soit simple; ou, ce qui est le même, si on suppose que les nombres λ & μ soient 5. & 1.

Il est donc sûr que cet illustre Auteur s'est trompé; mais c'est dans une chose extrémement délicate, & peut-être en confondant des lignes, qu'il est aisé de confondre ensemble dans le calcul, savoir des arcs de cercle avec leurs sinus. Ainsi il y auroit beaucoup d'injustice à juger, à cause de cette erreur, d'une maniére moins favorable de sa pénétration dans les Mathematiques. Les fautes de calcul & d'inadvertence nous sont fort pardonnables, & nous n'en faisons que trop souvent, pour peu que nous nous hâtions en des recherches difficiles. Elles ne deviennent capitales que quand on s'opiniâtre à les soûtenir, après qu'on a eu le temps de les reconnoître.

9) Allusion à la méthode pour les tangentes, mentionnée dans la Lettre N^o. 1912, ou à la méthode algébrique de Fatio, dont il parle encore dans la lettre à Huygens du 24 juin 1687 (voir le N^o. 2465, note 9), et qui d'ailleurs n'en pourra pas avoir différé beaucoup.