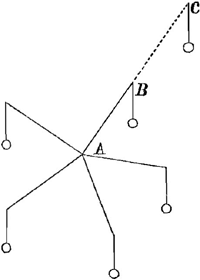
estoient chacun egaux aux perpendiculaires de B sur les lignes AN et qu'ainsi BA estoit le vray axe de pesanteur des fils. |
-
voetnoot1)
- Extrait du Livre F des Adversaria, p. 271.
-
voetnoot2)
- Christianii Hugenii Exercitationes Mathematicae, etc. Fasc. II, p. 56 et suiv.
-
einda)
- A, B, C puncta data in linea recta vel utcunqueGa naar voetnoot4) KDK curva ejusmodi naturae ut ductis ad ejus punctum quodlibet rectis AD, BD, CD harum summa
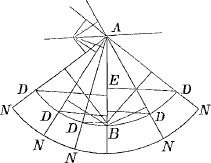
sit datae rectae aequalis. Quaeritur tangens in D.
Sit ea DE, et E punctum proximum D, idque censendum in curva existere. Ab E in rectas AD, BD, CD, si opus sit productas, cadant perpendiculares EG, EH, EF.
Ergo si ex A, B, C ducerentur rectae ad E, crescet ea quae ex C, longitudine DFGa naar voetnoot5), quae ex B diminuetur longitudine DH quae ex A diminuetur item longitudine DG. Ergo ut summa ductarum ex A, B, C ad E sit aequalis tribus ex A, B, C, ad D ductis, hoc est rectae datae, oportet DF aequari duabus DH, DG.
Sit tangenti DE perpendicularis DL, et ex D descripta conferentia secet rectas AD, BD, CD in M, O, N, unde ducantur in DL perpendiculares MQ, OR, NP. Quod si jam pro radio circuli sumatur DE, apparet angulorum DEF, DEH, DEG esse sinus DF, DH, DG. Istis autem angulis aequales sunt singulis singuli PDN, RDO, QDM, quorum sinus sunt NP, OR, MQ. Ergo sicut sinus DF aequatur duobus DH, DG, ita sinus NP aequabitur duobus OR, MQ. Unde facile colligitur punctorum M, O, N centrum gravitatis esse in recta DL. Itaque reperto hoc centro, dabitur recta DL, quae tangenti DE est ad angulos rectos. Eadem autem est constructio quotcunque data fuerint puncta ad D ducendae quarum summa sit data. [Christiaan Huygens].
-
voetnoot4)
- On remarquera que la démonstration qui va suivre s'applique, en effet, à une situation quelconque des points A, B, C, etc.
-
voetnoot5)
- En exprimant, comme le fait Huygens, par les projections de DE sur AD, BD et CD les variations a1, a2, a3, de ces trois lignes, résultant du déplacement DE, on peut ramener la solution du problème à celle d'un problème de statique, savoir: trouver la direction de la résultante d'un système de forces, n1P, n2P, n3P, etc. agissant sur le point D dans la direction des foyers, lorsque n1, n2, n3, etc. représentent le nombre des fils aboutissant aux divers foyers dans le problème corrélatif géométrique. En effet, de la condition n1a1 + n2a2 + etc. = 0, qui caractérise la courbe de von Tschirnhaus, il suit que la somme des moments virtuels, n1Pa1 + n2Pa2 + etc. des forces agissant sur le point D est nulle, lorsque ce point doit rester sur la courbe KK. Le point D est donc en équilibre et la résultante des forces doit être normale à la courbe. Toute propriété des composantes, données en grandeur et en direction, par rapport à la direction de la résultante, peut donc servir à la solution du
problème de von Tschirnhaus. Telle est l'égalité, à laquelle a songé Fatio, des moments des forces par rapport à un point de la résultante, de part et d'autre de cette ligne; ou encore la propriété de l'axe de gravité de masses proportionnelles aux forces et placées dans leurs directions à des distances égales du point d'application.
L'identité du problème de la normale à un point donné des courbes de von Tschirnhaus et de la détermination de la direction de la résultante de quelques forces n1P1, n2P2 etc. agissant sur ce point, se maintient encore dans le cas où les foyers ne seraient pas situés dans un même plan et que le point D décrirait une surface. Dans ce cas, évidemment, la normale de la surface coïncide avec la résultante des forces.
Il semble que des considérations analogues ont guidé Huygens dans la solution du problème de von Tschirnhaus. Dans la collection Huygens on rencontre un bout de papier, sur lequel Huygens a écrit la note suivante:
12 nov. 1687.
Si trahantur omnia fila aequalia ab aequalibus ponderibus, sitque A centrum gravitatis punctorum omnium extremorum seu linearum ipsarum aequalium, manebit nodus seu punctum A ex nostro theoremate (la Prop. II de son écrit: De potentiis fila funesve trahentibus. Chr. Hugenii Opera Varia, ed. 's Gravesande, Tome I, pag. 288). Hinc probari potest summam istam filorum aequalium esse minimam, quia alias pondera trahentia possent descendere mutato loco A nodi; et ideo descenderent.
Quod si ita manent, manebunt etiam licet aliqua fila producantur, ut AB in C. Ergo et linea AC cum reliquis est summae brevissimae.
Ergo quod in plano demonstratur ex problemate Tangentium Fatii et nostro, hic etiam in solido verum esse evincitur. Nempe, a punctis quotlibet in pleno aut solido spatio utcunque sitis ad punctum unum rectae lineae ductae ut sint simul sumptae omnium minimae, oportet punctum hoc esse centrum gravitatis partium aequalium eorum filorum quas abscindit superficies sphaerica circa ipsum tamquam centrum descripta.
Si ex loco A abductum eodem revertitur necesse est ex reversione filorum summam ad A ad puncta omnia simul imminuere, quia alias centrum gravitatis omnium ponderum non descenderet ut facile est ostendere.
-
voetnoot3)
- La phrase manque de clarté par suite de quelque confusion dans les termes employés. Dans le manuscrit elle est précédée d'un commencement de phrase que Huygens a biffé: De là il s'imagina en suite que le point B ne pourroit en tant que centre de gravité des dits points n.
|