Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 176]

N^o 2468.
E.W. von Tschirnhaus.
juin 1687.
Appendice I au No. 2467.

La copie¹⁾ se trouve à Leiden, coll. Huygens.

Responsio ad Reflexiones D.M.N. Fatij de Duillier supra methodum meam determinandi Tangentes Curvarum, qua publicata extat in lib. Med. Ment. et Corp.

Quamprimum has Reflexiones accepi eas attente pervolvi, et sane earum Authorem generosae admodum mentis esse plurimum gavisus sum, quique tam honeste mecum agit, ut meliorem meorum errorum censorem vix optare possem. Quare non dubito defensionem meam ipsi acceptam fore, cum ea non tam mei defensio quam ipsius veritatis sit, quam quantum per multa negotia licet, breviter sed clarè meo judicio, et sans aucune opiniatreté, manifestam faciam.

Notandum itaque.

1. Circa verba supposons que a et d dans-sera donc la tangente de la ligne courbe au point C, Reg. hanc tangentes determinandi, si meis curvis applicetur, quas pag. 68, 69 mei Tractatus exhibui, multo simpliciorem adhuc evadere. Cum enim juxta hunc authorem sit, ut numerus linearum ac ad numerum linearum cd, sic reciproce pn ad nm. Jam vero circa curvas meas loco modo citato^a) numerus linearum ab una parte semper aequalis est linearum numero ab altera parte. Nam in fig. 6^a dantur duae lineae; in 7^a quatuor; in 8^a sex, atque ita in infinitum; adeoque utraque ab parte aequo numero fila seu lineae. Hinc clarissime patet, lineam mp semper esse bifariam dividendam in n, circa meas curvas juxta hunc Authorem siquidem Reg. ejus legitima sit, hoc autem absolute falsum esse ostendam; adeoque Reg. hujus Authoris circa meas curvas (dico expresse meas curvas. nam num ea circa suas curvas bene habeat, jam examini non subjicio) excepto unico casu (de quo statim loquar) falsa est: id quod sic ostendo. Suppono in fig. 6^a in Ellipsi linea angulum ACB bifariam dividens sit perpendicularis ad tangentem in puncto C. Hoc jam mathematicis notum. Jam in fig. 7^a linea angulum CDB bifariam dividens juxta hunc Authorem et modo ostensa est perpendicularis tangenti curvam FDE^b) in puncto D; atqui ope filorum CDB describitur Ellipsis, quae secat curvam FDB in puncto D, ut attendenti statim perspicuum, cui proinde quoque linea bifariam

1) Elle est de la main de P. van Gent.

a) Hic Fatius etsi duos tantum focos ponit, tamen et eos casus comprehendere voluit ubi plures sunt foci, sed quorum aliqui in idem punctum incidere ponuntur. Veluti cum in fig. 7⁶⁾ A cadit in B, vel in fig. 8^a A et B in D vel in C. [Chr. Huygens].

6) Voir les figures de la pièce No. 2461.

b) Non hoc dicit Fatius quando puncta A E C tres focos constituunt [Christiaan Huygens].

[p. 177]

dividens ang. CDB est perpendicularis tangenti ad Ellipsin in puncto D juxta modo suppositum. Adeoque curvae se invicem secantes possunt in puncto sectionis unam et eandem perpendicularem habere ad tangentes in puncto sectionis, quod est absurdum, adeoque Reg. hujus authoris est falsa; si dicat ang. ADB juxta suam Reg. generalem esse bifariam dividendum idem absurdum provenit, adeoque patet propositum. Cum itaque clarum sit, quod Reg. generalis ducendi tangentes D. Fatij, si ad meas curvas referatur sit falsa, adeoque conclusio generalis in demonstratione sua erronea; quaeritur ubinam in praemissis, unde hanc deduxit, author hic erraverit?

2. Hoc autem non difficulter Lector deteget, si pag. 2 haec verba perpendat, dicit enim: Soit λ le nombre qui exprime etc. à toute la longueur du fil qui est donnée. Hoc si lector applicabit in meo Tractatu fig. 7 et 8, et quatenus tales curvae in infinitum concipi possunt, videbit, hoc nullo modo verum esse, nisi statuat ex. gr. in fig. 8 omnes focos coincidere in duos focos A et B, tunc haec res utique se sic habet; verum si infinita talia fila coincidunt in duos focos A et B curva quae describitur (quotquot sint numero fila) non est alia quam Ellipsis (ut parum attendenti erit clarissimum) patet itaque

1. Quod demonstratio authoris sit quidem legitima, sed si ad meas curvas applicetur nihil aliud demonstravit, quam quod in fig. 6^a Ellipsi nimirum linea bisecans ang. ACB sit perpendicularis tangenti in puncto C, id ipsum quod mea Reg. quoque requirit.

11. Quod conclusionem ejus, si ad meas curvas referatur, universaliorem fecerit, quam praemissa requirunt, et in eo error ejus consistit: nam licet infinita fila supponat, si coincidant in duos focos (quod necessarium si praemissae verae debent esse prout modo ostendi) non aliae ac aliae novae curvae describantur prout plura aut pauciora sunt fila, sed unica illa et eadem Ellipsis.

111. Patet quoque quod nullius ideo erroris me convicerit, nihil nempe mihi contrarium statuit, si demonstratio ejus, quatenus est legitima consideretur, et meis applicetur, prout modo ostendi.

1111. Patet tandem quod methodus ejus Tangentes curvarum designandi, non sit universalis pro meis curvis exhibitis; adeoque nullo modo nec simplicior nec generalior methodo mea exhibita. Sed de hoc plura in seqq.

3. pag. 5. dr. la methode de M. de T. etc. perpendiculaire sur la courbe^c). Fateor me haec verba non potuisse satis admirari. Nam certum est, quod nec quidem unquam de hac re cogitavi, nec quoque hanc Reg. in meo Tractatu publicavi²⁾, cum prorsus contraria ibi habeantur (vid. pag. 74. fig. 19) nec quoque ulli homini haec communicavi, a quo D. Fatio talia potuisset impetrare. Patet itaque quod

c) Videris itaque tuam ipsius regulam non intelligere. Nam si in fig. 19 coincidant puncta C D vel in fig. 8 coincidant puncta A,B,D vel A,B,C, jam tua constructio eo redit quo eam redire ait Fatius [Christiaan Huygens].

2) Consultez la note 7 de la pièce N^o. 2460.

[p. 178]

omnes consequentiae, quas hinc deducit, hoc supposito tanquam vero, falsae sunt, nec ad me quicquam spectant.

4. Ad verba pag. 6. Cela paroitr a davantage etc. extremement facile à resoudre, haec notanda habeo, magnam mihi esse suspicionem, quod demonstratio hujus Theorematis quod proponit aliquid falsi includat: alias etenim absque dubio errorem suum animadvertisset, quam annot. 1^a et 2^a manifestum feci. Hoc nimirum Theorema si parum mutetur^d) et simpliciori formâ proponatur accurate mea quae publicavi pag. 74 in meo Tractatu confirmant. Hinc itidem elucescit, quod in infinitum nil aliud opus quam continua bisectione^e) sit³⁾, prout dixi in eadem pag. ad mearum curvarum tangentes determinandas, qua methodo dubito num facilior poterit exhiberi. Sed ne haec gratis dixisse videar, aliquo modo clarius me explicabo. Sint puncta ABCDE etc. ad libitum assumpta, applicentur his fila ea ratione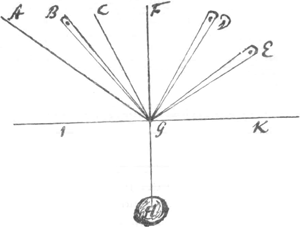



prout in meo Tractatu ostensum, et in praesenti fig. repraesentatum appendatur jam omnibus hisce filis pondus H; dico quod ubi hoc pondus quiescet, linea FHG perpendicularis erit ad tangentem curvae IGK in puncto G^f). Habebunt hic alij fontes inventionis (quos Eruditi alijs non libenter communicant) ex quibus mea examinare poterunt, num se recte habeant nec ne: unde quoque Reg. meam universalem ducendi tangentes?^g) (quam ob rationes ex parte exhibui) proprio marte poterint detegere, quod majori cum fructu et voluptate fiet, quam si hoc ex me ipso didicissent.

5. Ad verba pag. 7. En effect on peut etc. veritablem. fort composé haec respondeo, quod methodus curvarum Geometricarum sit Problema per solas rectas lineas solu-

d) Imo nihil est mutandum [Christiaan Huygens].

e) Bisectione non tamen auguli aut arcus sed linearum rectarum [Christiaan Huygens].

3) Voir la note 1 de la pièce N^o. 2461.

f) Hoc verum quidem sed nihil ad propositum [Christiaan Huygens].

g) Sed haec tua universalis regula falsa est [Christiaan Huygens].

[p. 179]

bile: Hoc facillime derivatur^h) ex methodo Cartesij⁴⁾, item ex mea methodo⁵⁾, publicata in Actis Erudit. Lipsiensibus Anni 1682. pag. 391. Hoc statim est perspicuum. Quod vero etiam curvarum mechanicarum tangentes determinare sit problema simplex forte primus in meo Tractatu docui. Verum licet haec se ita habeant, nullo modo mihi contraria sunt: nam divisio arcus circularis bifaria quam solam adhibendam esse dixi pag. 74ⁱ⁾ est quoque problema unius dimensionis. Nihil aliud supponit quam subtensae bifariam divisionem; adeoque mea methodus non est magis composita quam decet. Adde quod et falsa consequentia hic occurrit: nam supponamus me ad meam methodum tangentium supponere arcum in data ratione esse dividendum (quod tamen mihi nunquam in mentem venit uti ex annot. 3^e clarum) et alium quempiam ostendere, hoc problema simplex seu unius esse dimensionis, hinc non unicè absolute poterit concludere, me ideo errasse: nam omnia simplicia problemata etiam per magis composita solvi queunt, ex. gr. ope Circuli, Parabolae, Conchoidis etc. Sed non contra. Adeoque hoc tantum potest concludi, me compositam magis viam adhibuisse, cum tamen simplicior detur. Unde nec haec, quae author hic contra me profert, ullius me erroris convincunt.

6. Ad verba pag. 8. Je say bien usque λ et μ soient 5 et 1. Hic fatetur ipse Author harum Reflexionum me dixisse non nisi bisectionem esse adhibendam; sed hoc tali ratione proponit, quasi id non expresse, sed quasi tecte hoc proposuissem, cum tamen expressissimis verbis extet pag. 74. Atque ita possem progredi^k) etc. poterit clarius quid scribi. Verum quia hoc adversatur ijs quae modo dixerat, quod Ego arcum in data ratione secandum dixeram, partim ijs, quibus me convincere volebat, me admodum compositam viam inijsse, praecipue vero quia hoc adversatur Reg. suae datae, qua lineae potius rectae in data ratione divisionem solum opus esse praetendit, hasce ob causas porro me convincere vult, hoc non posse esse, quod clarum putat ex eo si casus ponatur ubi fila ab una parte sint ad fila alterius partis, ut 5 ad 1. Verum hoc nunquam circa hanc methodum, ope cujus curvas designo, posse accidere, attendenti manifestum erit, et ex eo quod supra annot. prima dixi^l); nam semper ab utraque parte filorum numerus est aequalis; unde nunquam potest esse ut sit 5 ad 1. Adeoque haec quoque nullo modo convincunt me falsa dixisse, dum non nisi bisectionem sufficere docui.

7. Credo itaque ex his perspicuum esse, Authorem harum Reflexionum hujus meae methodi non solum simplicitatem, sed et ejusdem universalitatem nullo modo perspexisse, alias ea quae publicavit meis pag. 2 non protulisset. Nam hic

h) In quibusdam difficillime vel prorsus non [Christiaan Huygens].

4) Il s'agit de la méthode bien connue pour mener les normales aux courbes algébriques, que Descartes a décrite dans le livre deuxième de sa ‘Géometrie’.

5) Voir la Lettre N^o. 2274, note 8.

i) Sed in curva fig. 8 opus erit trisectione anguli [Christaan Huygens].

k) Sed quod ibi dicis falsum est [Christiaan Huygens].

l) Hic non attendisti fila C,D, in idem posse incidere in fig. 19. Vel fila A,B,C, aut A,B,D in fig. 8 [Christiaan Huygens].

[p. 180]

non solum simplici bisectione curvarum omnium Geometricarum, et infinitarum Mechanicarum, sed absolute omnium curvarum, quae concipi possunt, unico ductu descriptae esse, tangentes determinantur, quo Theoremate nescio num universalius et utilius tota Geometria habeat.

6) Voir les figures de la pièce No. 2461.