Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2465.
N. Fatio de Duillier à Christiaan Huygens.
24 juin 1687.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
Elle fait suite au No. 2456.
Chr. Huygens y répondit par le No. 2473.

Monsieur

J'ai sçû de Monsieur Boile que vôtre santé étoit bien retablie et même que vous aviez repris vos études. Celui de qui nous avons ces bonnes nouvelles étoit venu depuis peu de Hollande. Je croi qu'il est déja parti pour y retourner, mais comme je ne l'ai pas veu je n'ai point pu profiter de son depart pour vous dire des nouvelles de l'Angleterre. Je me suis déja trouvé trois fois à la Societé roiale où j'ai entendu proposer tantôt d'assez bonnes choses et tantôt d'assez mediocres. Quelques uns de ces Messieurs qui la composent sont extremement prévenus en faveur d'un livre

1) Christiani Hugenii etc. Exercitationes Mathematicae Fasc. II, p. 99.

[p. 168]

de Monsr. Newton²⁾ qui s'imprime presentement³⁾ et qui se debitera dans trois semaines d'ici. Ils m'ont reproché que j'étois trop Cartesien et m'ont fait entendre que depuis les meditations de leur auteur toute la Physique étoit bien changée. Il traitte en general de la Mechanique des Cieux; de la maniere dont les mouvemens circulaires qui se font dans un milieu liquide se communiquent à tout le milieu⁴⁾; de la pesanteur et d'une force qu'il suppose dans toutes les planetes pour s'attirer les unes les autres. Il démontre ce que vous avez trouvé touchant la cycloïde et les pendules, et il determine des epicycloïdes qu'il faut lui substituer si on suppose que le centre de la Terre soit fort voisin⁵⁾. Il donne le moien de decrire une surface d'un verre qui serve avec une autre surface donnée pour rassembler les raions qui partent d'un point donné precisement en un autre point. Sa methode concourt avec la vôtre pour la construction car il se trouve que tous les raions emploient un temps égal pour venir d'un point à l'autre⁶⁾, mais ses demonstrations dependent de tout un autre principe. Il avance cette proposition⁷⁾, que la resistance que sent un globe qui se meut dans un liquide, n'est que la moitié de celle que ressentiroit un grand cercle de ce globe, qui se mouvroit suivant son

2) Philosophiae Naturalis Principia Mathematica. Auctore Js. Newton, Trin. Coll. Cantab. Soc. Matheseos Professore Lucasiano, & Societatis Regalis Sodali. Imprimatur. S. Pepys, Reg. Soc. Praeses. Julii 5. 1686. Londini, Jussu Societatis Regiae ac Typis Josephi Straeter. Prostant Venales apud Sam. Smith ad insignia Principis Walliae in Coemiterio D. Pauli, aliosq; nonnullos Bibliopolos. Anno mdclxxxvii. in-4^o.

3) L'impression du troisième livre des ‘Principia’, dont le manuscrit avait été achevé en mars 1687 et présenté à la Société Royale dans sa séance du 6 avril suivant, fut terminée au commencement de juillet.

4) Allusion à la Section VIII, Livre II: ‘De Motu per Fluida propagato’, qui traite de la propagation des ondes, ou à la Section suivante: ‘De motu Circulari Fluidorum’, qui se rapporte à des mouvements rotatoires dans un fluide visqueux, comparables aux tourbillons Cartésiens.

5) Il s'agit ici des Propositions L-LII du Livre I^er, dans lesquelles Newton traite des isochrones hypocycloïdales propres au cas d'une force proportionnelle à la distance du centre, comme il se présenterait dans les cavités d'une Terre homogène. De ces propositions plus générales Newton déduit, dans le corollaire 2 de la proposition LII, l'isochronisme de la cycloïde, appliqué dans les arcs cycloïdaux du pendule de Huygens.

6) La construction, décrite par Newton dans sa Proposition XCVIII du Livre I^er Section XIV, est, en effet, conforme à celle que Huygens donna au Chapître VI de son Traité de la Lumière. Toutefois le théorème simple et élégant de Huygens, d'après lequel tous les rayons emploient un temps égal pour venir d'un même point à un autre, n'a pas été formulé par Newton et ne pouvait pas l'être par lui, parce qu'il ne s'accorde pas avec la théorie corpusculaire de la lumière exposée par Newton dans la Section citée. En effet, d'après cette théorie, l'indice de réfraction d'une substance serait proportionnel à la vitesse de la lumière dans son intérieur, tandis que le théorème de Huygens exige qu'il lui soit inversement proportionnel.

7) Proposition XXXV, Livre II, Section VII. Si Globus & Cylindrus aequalibus diametris descripti, in Medio raro et Elastico, secundum plagam axis Cylindri, aequali cum velocitate celerrime moveantur: erit resistentia Globi duplo minor quam resistentia Cylindri.

[p. 169]

axe, avec la même vitesse. Ce traitté que j'ay veu en partie est asseurement tres beau, et rempli d'un grand nombre de belles propositions, mais je souhaitterois, Monsieur que l'Auteur vous eut un peu consulté sur ce principe d'attraction qu'il suppose entre les corps célestes. On m'a dit qu'il expliquoit assez bien par là le flux et le reflux de la mer⁸⁾, savoir en supposant que la Terre et la Lune s'attirent l'une l'autre. J'avois déja remarqué en Hollande que l'on pouvoit rendre des raisons assez probables du flux et du reflux en supposant vôtre explication de la pesanteur et en imaginant qu'il y a une cause semblable qui produit une pesanteur dans la Lune. Car il resulte de là qu'effectivement la Terre et la Lune s'attirent un peu l'une l'autre et que nous devons avoir la haute mer quand la Lune est au meridien, ou plûtôt, comme il paroit par les observations, deux ou trois heures après qu'elle l'a passé. Vous vous souvenez Monsieur de la methode algebraïque dont je me servois pour determiner les tangentes⁹⁾ des lignes courbes dont l'equation est donnée. Comme cette methode est veritable elle concourt entierement avec la vôtre¹⁰⁾, mais elle a ceci de commode pour moi qu'elle depend d'une reflexion fort simple et fort facile a retenir. C'est ce qui me fit resoudre il y a quelque temps à la mettre au net et à en faire quelque usage. Pendant que je me suis occupé à cela, je me suis attaché en même temps à resoudre cet autre probleme; La proprieté des tangentes d'une courbe etant donnée trouver l'equation de la courbe. J'ai trouvé en quelque sorte le moien de le resoudre toutes les fois qu'il est possible, et de reconnoitre quand la courbe proposée n'est pas Geometrique. Veritablement j'ai besoin que les proprietez des tangentes soient exprimées par la proportion qui se trouve entre deux lignes particulieres paralleles à des lignes données; mais c'est ce qui est toujours assez facile.

Voici des exemples de quelques uns de mes calculs.

Le point A et les lignes x, y etant donnez de position trouver l'équation de la ligne courbe qui passe par A et dont les tangentes comme BAC. ont toutes cette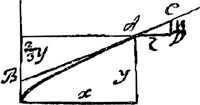



proprieté que la ligne AD parallele à x est a DC parallele à y comme x est à ⅔y. Je fai mon calcul comme il suit¹¹⁾ z. u∷x. ⅔y.

3 u x - 2 zy = 0.

+ 3 - 2

8) Proposition XXIV, Livre III: Fluxum et refluxum Maris ab actionibus Solis ac Lunae oriri debere.

9) Nous ne connaissons pas cette méthode algébrique de Fatio, qu'on ne doit pas confondre avec les considérations géométriques qui l'ont conduit à la construction des tangentes des courbes focales de von Tschirnhaus, communiquée dans la ‘Bibliothèque Universelle’ du mois d'avril 1687 (voir la pièce N^o. 2460).

10) La ‘Regula ad inveniendas Tangentes linearum curvarum’ de Huygens; voir la Lettre N^o. 1912, note 7.

11) On reconnaîtra facilement que la méthode de Fatio se fonde sur la remarque que l'expression pydx+qxdy, multipliée par x^p-1y^q-1, se transforme dans la différentielle totale de x^py^p. Huygens dans sa lettre à de l'Hospital, du 23 juillet 1693, a donné une exposition détaillée de cette méthode.

[p. 170]

y³/x² doit toujours être égal à une même grandeur par exemple à g; car g est donnée à cause que x et y sont donnez pour un cas, ce qui suffit.

Donc l'équation cherchée est y³ - gx² = 0.

Si j'avois z. u ∷ b-y. x-c mon calcul devroit être comme il suit + zx - zc - bu + uy = 0.

+ ½ x² - cx - by + ½yy = gg Equation cherchée.

Si j'avois z. u ∷ b - y + 2x.x - c + 6y.

+ zx - cz + 6yz - bu + yu - 2xu = 0....A.

+ ½x² - cx - by + ½y². Partie des termes de l'equation cherchée.

+6 -2

+6.-2 ∷ + 3.-1 en divisant les premiers termes par 2.

+ 2x³/y. Si ce terme ci étoit dans l'equation cherchée il donneroit dans l'équation A les termes + 6xxz/y - 2x³u/yy qui sont entre eux comme 6yz - 2xu, au lieu qu'il devroit donner les termes mêmes 6yz-2xu à cause des autres termes de l'equation A qui ont déja leurs correspondans. Donc il n'y a point de ligne courbe geometrique de qui les tangentes aient la proprieté proposée¹²⁾.

Le chevalier Gordon¹³⁾ a trouvé une construction de pompe pour les vaisseaux qui fait un effet prodigieux.

Si vous étes encore dans le dessein Monsieur de me donner un exemplaire de

12) Il est à peine nécessaire de faire voir ce que cette conclusion a de prématuré. Voici un exemple qui en démontre l'inexactitude. A l'équation xdx + ydx - xdy + ydy + a² / x dy = 0 il est satisfait par le cercle x² + y²-a² = 0.

13) Sir Robert Gordon, né le 7 mars 1647, fils aîné de Sir Ludovick Gordon, baronet of Gordonstoun, Drainie, Elginshire. Il s'appliqua à la mécanique et la chimie et fut en correspondance stoun, Drainie, Elginshire. Il s'appliqua à la mécanique et la chimie et fut en correspondance avec Robert Boyle. La pompe qu'il inventa attira l'attention par la facilité de la manoeuvre et le rendement favorable. Toutefois, faute d'encouragenment, la construction resta un secret, gardé dans la famille. Robert Gordon devint chevalier en 1673 et succéda comme baronet à son père en 1685. Il était un favori de James II, fut élu membre de la Société royale, le 3 février 1686, et mourut en 1704.

[p. 171]

vôtre traitté de la pendule je vous prie de le remettre à celui qui vous fera tenir cette lettre. Je suis avec un profond respect

Monsieur

Votre treshumble et tresobeissant serviteur N. Fatio de Duillier.

A Londres chés Mrs. Barthelemi et Nicolas Midy Banquiers ce 14/24 Juin 1687.

A Monsieur

Monsieur Huijgens de Zulichem à La Haïe.