|
| |
| |
| |
No 2625.
Christiaan Huygens.
[septembre 1690].
Appendice II au No. 2623Ga naar voetnoot1).
Le manuscrit se trouve à Leiden, coll. Huygens.
Il a été publié par D.J. KortewegGa naar voetnoot2).
| |
§ I.
Fundamentum omnium eorum quae de curvae catenae reperimusGa naar voetnoot3).
Fili gravitate carentis, et aequalia ponder a innexa habentis, tria qualibet internodia continua ac sursum tendentia ita ad planum horizontale inclinantur, ut tangentes angulorum hujus inclinationis crescant aequali excessuGa naar voetnoot4)
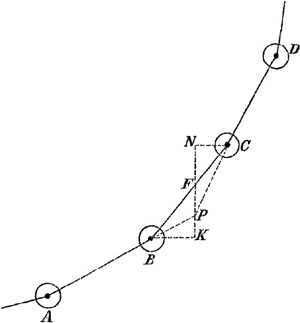
Fig. 1
| |
| |
Sint catenae pondera aequalia innexa habentis A, B, C, D, internodia tria sursum tendentia AB, BC, CD, producanturque internodia extrema et conveniant in P. Et per P ducatur ad horizontem perpend. NPK eique occurrant horizontales BK, CN. Est ergo internodii AB inclinatio ad horizontem angulus PBK, et internodii BC inclinatio angulus FBK, et internodii CD inclinatio angulus PCN. Dico itaque tangentem ang.i PBK tantum superari a tangente ang.i FBK quantum haec superatur à tangente ang.i PCN.
Quia enim concursus rectarum AB, DC, hoc est punctum P incidit in perpendicularem horizonti quae per centr. gr. ponderum BC transit; sunt autem pondera haec aequalia, necesse est perpendicularem KPN secare internodium BC aequaliter in F, unde et BK, CN aequales erunt. Quarum utrovis pro radio adsumta, apparet PK tangentem anguli PBK eadem recta PF superari a tangente ang.i FBK, qua tangens hujus anguli, sive illi aequalis, FCN superatur a tangente ang.i PCN. Sunt autem hi anguli ut jam diximus inclinationes internodiorum AB, BC, CD ad planum horizontis. Ergo constat propositum.
Catenae seu fili suspensi aequalia pondera innexa habentis, si infimum internodium horizonti parallelum fuerit erunt deinceps anguli reliquorum internodiorum cum horizontali plano tales, ut eorum tangentes crescunt secundum rationem numerorum ab unitate incipientium 1, 2, 3, 4, 5, etc.
| |
Catena composita ex virgulis aequalibus WS, SP, PG, GB et dimidia BA, quae horizonti parallela. AB = a. AC = b.
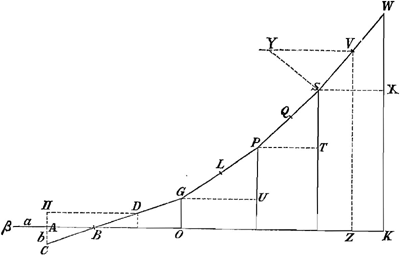
Fig. 2.
| |
| |
Angulorum GBO, PGU, SPT, WSX, etc. tangentes aequaliter crescunt.
GO ad OB ut b ad a,
PU ad UG ut 2b ad a,
ST ad TP ut 3b ad a,
WX ad XS ut 4b ad a.
Hoc facile absque calculo potest demonstrari. Vid. p. 92Ga naar voetnoot6).
YS ad SV ut WX ad XS ducta scilicet SY perpend. in SW er VY parall. XS.
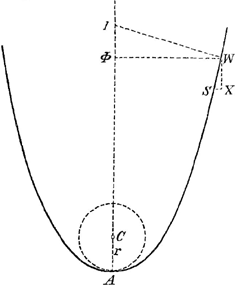
Fig. 3.
YS ad SV ut 4b ad a,
sed SV = a,
YS = 4b
cGa naar voetnoot7) = longitudo catenae WA,
½c:SV = YS(4b):AC(b) = SY.SV/½c, facile enim apparet toties contineri SV in ½ c sive dimidia longitudine catenae, quoties b sive AC continetur in SY.
Ergo et AΠ = 2.YS.SV/c, ducta DΠ parall. BA. Ducta est enim curva quae tangit rectam AB in A, BG in D, GP in L, quam pro curva catenae hic habeo, et quam pro circumferentia circuli, aut etiam parabola, reputo, cujus circumferentiae diametrum hic porro investigoGa naar voetnoot8).
b = AΠ = 2.YS.SV/c: ADGa naar voetnoot9) (2a) = AD (2a): diam.
| |
| |
diam. = 2c.SV/YS, nam 2SV = AD,
½ diam. = c.SV/YS = r
Sed ut YS ad SV ita WX ad XS et ita WΦ ad ΦIGa naar voetnoot10). Ergo c.ΦI/WΦ = r radius curvitatis in A. Theorema praecipuumGa naar voetnoot11).
| |
25 Sept. 1690.
Sit in puncto curvae aliquo K recta KE (fig. 4) ipsi ad ang. rectos quae conveniat cum axe in E, et a C, centro curvitatis in A, ducatur CI parallela KE, usque ad
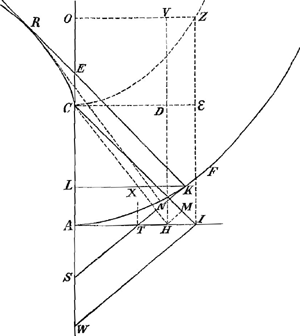
Fig. 4.
| |
| |
tangentem in vertice AI. Dico rectam AI aequalem fore curvae AK. Nam quia perp. KL ad LE ut curva AK ad AC, ut dictum pag. 3a ante hanc.Ga naar voetnoot13). Ut autem KL ad LE ita est IA ad AC; erit curva AK ad AC ut recta IA ad AC, ideoque curva AK aequalis rectae IA.
Ergo si F sit punctum curvae ubi illius tangens inclinatur ad plan. horiz. angulo semirecto, erit curva AF aequalis recto AC.
| |
Ex C ducantur CH, CI minimum angulum ad C constituentes. Sitque NR parall. HC, eademque curvae AK ad ang. rectos. Item KR parall. IC, eademque curvae ad ang. rectos. Erit jam AN = AH, et AK = AI ex superius traditis. Unde NK = HI.
IW est perp. CI, itemque HM. Cumque sicut KN ad MH, hoc est IH ad MH, ita sit KR ad MC seu KR ad IC ut WI ad IA (nam ut IH ad HM ita WI ad IA) sive ut WC ad CI. Itaque WC aequ. KR, hoc est = AC + curva CR, et ablata communi CA, sit curva CR = AW.
| |
Cumque angulus NRK sit aequalis HCI propter parallelismum continentium, erit triang. NRK ad triang. HCI sive HCM (ducta HM perp. in CI) sicut quad. NR ad quad. HC, seu ut quad. KR ad quad. IC, nam IC, HC aequales propter angulum in C minimum.
Sed KR est aequ. CW. Ergo triang. KRN ad triang. ICH ut qu. WC ad qu. CI, hoc est ut WC ad CA.
Si IZ ponatur = CW, erit Z ad parabolam vertice C, axe CO, latere recto CAGa naar voetnoot16). Et quia triang. KRN ad ICH ut WC ad CA, hoc est ut ZI ad Ie, hoc est ut ▭ ZH ad ▭ εH; estque ▭ εH = duplum triang. ICH, erit et ▭ ZH duplum triang. KRN. Atque ita spatium totum ACRKA dimidium spatii ACZIA, quod aequale rectangulo AD cum tertia parte rectang. CZ. Itaque
| |
| |
spatium ACRKA aequale triangulo ICA + ⅓ triangulo IAW, hoc est ½ cr + + ⅙ ceGa naar voetnoot17).
| |
Sit KS tangens in K. Dico superficiem genitam ex conversione curvae AK circum axem AC, aequari circulo cujus radius medius proportionalis sit inter AC et duplam AS. Unde patet curvas ex conversione KA et FA circa axem AC, esse inter se sicut AS, AG quas abscindunt tangentes in terminis K et F.
Demonstratur ex eo quod si ex T intersectione tang. duum AT, KS ducatur TX axi parall., ea debet transire per centrum gravitatis curvae AKF quia tangentes in K et A; hoc est fila catenam FKA sustinentia conveniunt in T.
Jam ut KL ad LE, hoc est ut SL ad KL, sive ut SA ad AT, ita curva KA ad AC ex supradictisGa naar voetnoot19). Unde quod fit ex SA in AC aequ. facta ex AT in curvam AK, ideoque superficies ex conversione curvae AK aequalis cylindricae superficiei cujus altitudo AC, semidiameter basis AS, hoc est circulo cujus radius media prop. inter AC et duplam AS.
| |
Angulorum GBO (fig. 2), PGU, SPT, WSX, etc. tangentes aequaliter crescunt, atqui BG, GP, PS, SW sunt aequales. Ergo GO, PU, ST, WX sunt sinus angulorum quorum tangentes aequaliter crescunt et BO, GU, PT, SX eorundem angulorum sunt sinus complementorum.
Ut inveniatur summa omnium sinuum ut σε, ΠΔ (fig. 5), quorum tangentes respectivae crescunt aequaliter, accipiuntur iisdem sinubus aequales in rectis ρχ, λμ atque ita fit ut summa sinuum quaesita (puta arcus αζ) ad totidem radios, sit ut spatium δωΘζ ad ▭ αζGa naar voetnoot21).
| |
| |
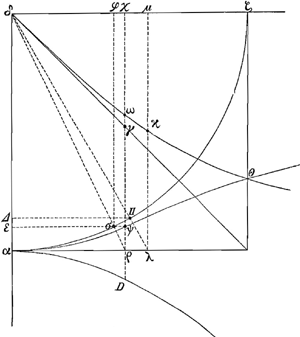
Fig. 5.
Constructio curvae δΘ
x = δχ = χγ = ψε,
y = ωχ = σε,
σδ = a,
ρδ = √ aa + xx,
√aa + xx∶a = x∶yGa naar voetnoot22).
| |
| |
| |
Summa sinuum compl. pro tangentibus aequaliter crescentibus (puta arcus αζ) est ad totidem radios ut spat. αΘζδ ad ▭ αζ, nam ipsi sinus compl. accipiuntur in rectis aequaliter distantibus respectivis, ita nempe ipsi σφ aequalis ψχ in recta ρχ.
Constructio curvae αΘ
ρδ∶grδ = ρχ∶ψχ quae itaque aequalis σφ
√aa + xx∶a = a∶y,
aayy + xxyy = a4,
yy = a4 / aa + xx curva αΘ.
Si itaque αD sit hyperbola aequilatera et sint proportionales Dχ, ρχ, ψχ erit punctum ψ in curca αΘ; nam qu. Dχ = qu. δχ + qu. ρχ.
| |
Ex sinubus qui conveniunt tangentibus Tabularum, inveniuntur sinus qui conveniunt tangentibus proximis aequaliter crescentibus.
| |
| |
Idemque in sinubus complementis.
| |
sinus |
½r |
50000 |
| 12500Ga naar voetnoot25) |
12406 |
1 |
99228 |
| 25000 |
24253 |
2 |
97014 |
| 37500 |
35113 |
3 |
93636 |
| 50000 |
44722 |
4 |
89442 |
| 62500 |
53001 |
5 |
84799 |
| 75000 |
60000 |
6 |
80000 |
| 87500 |
65850 |
7 |
75257 |
| 100000 |
35356 dimidium 70711 |
½ 8ae |
35356 |
| |
_____ |
|
_____ |
| |
330701 |
|
704732 |
| |
| 800000:330701:704732 = 1000000:41338:88091Ga naar voetnoot26). |
|
-
voetnoot1)
- Cet appendice contient la solution du problème de la chaînette telle qu'elle avait été trouvée de premier jet en septembre 1690 (voir la Lettre No. 2623, note 9), et formulée dans l'anagramme, dont nous avons donné l'explication dans l'Appendice précédent. On verra dans la suite que Huygens a commencé bientôt à la retoucher et améliorer. Dans la forme où nous la reproduisons elle a été recueillie sur diverses pages du livre G. Pour obtenir plus d'uniformité dans les notations, qui ont varié dans le cours des recherches de Huygens, nous nous sommes permis d'y apporter quelques changements dont, d'ailleurs, nous avertirons le lecteur dans les notes. De plus, nous avons ajouté une division en paragraphes pour faciliter les renvois.
-
voetnoot3)
- La rédaction de ce paragraphe qui se trouve à la page 97 du livre G, est d'une date postérieure à celle des parties qui vont suivre et qui supposent la connaissance du théorème qu'on y démontre. Probablement Huygens n'a pas jugé nécessaire d'abord de jeter sur le papier les raisonnements qui l'y avaient conduit.
-
voetnoot4)
- On remarquera que, en langage moderne, ce théorème, appliqué à la chaînette, revient à l'équation bien connue:
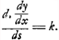
-
voetnoot5)
- Ce paragraphe contient la rectification de la chaînette, la démonstration du premier théorème de l'anagramme et l'introduction du rayon de courbure du sommet comme paramètre. Ces différentes parties sont dispersées sur les pages 57 et 58 du livre G. Autant qu'on en peut juger, elles représentent le commencement des recherches de Huygens sur le problème de la chaînette. En haut de la page 58 on lit encore les phrases suivantes, qui nous apprennent dans quel esprit ces recherches ont été entreprises:
‘Definiendum quid petatur cum proponitur invenienda curva secundum quam catena flectitur. An ut positis x et y normalibus, ita ut x a puncto in data recta accipiatur, aequatione aliqua referatur x ad y. An ut posita quadratura circuli vel hyperbolae possent curvae quaesitae puncta quodlibet reperiri. An ut posita dimensione spatii alicujus denique, puncta ista inveniri queant. An sufficit proprietates aliquas ejus curvae invenire’.
-
voetnoot6)
- Cette page est identique avec la page 97 d'où nous avons emprunté le § I.
-
voetnoot7)
- Le manuscrit a partout dans ce paragraphe l au lieu de c.
-
voetnoot8)
- C'est donc ici que le rayon de courbure du sommet est introduit comme paramètre de la chaînette.
-
voetnoot9)
- Chr. Huygens ajouta encore: ‘Nota quod AD considero tanquam 2a seu duplam AB.’
-
voetnoot11)
- Le théorème est identique avec le premier théorème de l'anagramme. En effet, d'après ce dernier, r = KL/LS. c (voir la figure de l'Appendice I) = LE/KL. c = ΦI/WΦ. c.
-
voetnoot12)
- Suite de la rectification de la chaînette. Cas particulier où la tangente fait un angle de 45o avec l'arc de la chaînette. Ce paragraphe est emprunté à la page 59. Il y est accompagné d'une figure identique au fond avec la partie correspondante de la figure du paragraphe qui suit, mais qui en diffère notablement quant aux lettres qui servent à désigner les points correspondants. Pour épargner au lecteur la confusion qui en pourrait résulter, nous avons préféré d'employer pour les deux paragraphes la figure du § IV, dont les notations sont conformes à celles de la figure de l'Appendice I, et d'apporter les changements qui en résultent dans le texte du § III. Pour reconstituer le texte primitif on n'a qu'à remplacer dans la figure et dans le texte les lettres K, E, I, L par N, P, H, O.
-
voetnoot13)
- C'est-à-dire dans le paragraphe précédent. Consultez la note 11.
-
voetnoot14)
-
Rectification de la développée. Démonstration du deuxième théorème de l'anagramme. Le texte et la figure 4 sont empruntés à la page 59 verso du livre G. Quelques lettres (T, X et E), et la ligne TX, ont été ajoutées à la figure pour l'accommoder au texte des autres paragraphes où nous l'avons employée.
-
voetnoot15)
-
Quadrature de la figure mixte ACRKA. Démonstration du troisième théorème de l'anagramme. Ce paragraphe est emprunté à la page 59 verso.
-
voetnoot17)
- Ici e représente l'arc CR de la développée, qui, d'après le paragraphe précédent, égale AW.
-
voetnoot18)
-
Quadrature de la surface de révolution de la chaînette. Démonstration du quatrième théorème de l'anagramme. Ce paragraphe se trouve à la page 59 recto. Des changements dans la notation y ont été apportés pour la raison mentionnée dans la note 12. Pour le reconstituer dans sa forme primitive on doit remplacer dans la figure 4 et dans le texte les lettres K, S, L, F, G, par F, G, V, N, S. Tout ce paragraphe avait été biffé, mais Huygens ajouta plus tard: ‘non delenda. sunt enim vera’.
-
voetnoot19)
- Voir le § III. D'après ce paragraphe l'arc KA égale IA; mais on a évidemment IA:AC = KL:LE.
-
voetnoot20)
-
Construction de la courbe xxyy = aaxx - aayy de l'anagramme, dont la quadrature permet de trouver le rapport de l'ordonnée AL. (fig. 4) à l'arc AK de la chaînette pour un angle donné de la tangente KS avec la ligne horizontale. Le paragraphe a été emprunté aux pages 58 recto et 61 recto.
-
voetnoot21)
- En effet, si l'on fait subir à la ligne αϱ des accroissements petits et égaux, il est clair d'abord que les tangentes des angles αδσ s'accroissent de même avec des quantités égales. Mais alors la somme des sinus de ces angles, multipliée par le petit accroissement que nous avons supposé, sera représentée par l'aire de la courbe δωϰμ, et la somme de leurs rayons, multipliée par la même quantité, par le rectangle αϱλμ. D'un autre côté, il s'ensuit facilement du théorème qui se trouve en tête de ce paragraphe que le rapport de l'ordonnée VZ (fig. 2) et de l'arc AV de la chaînette, pour un angle WSX = αδ Π donné, est égal à celui de la somme de ces sinus à la somme de leurs rayons.
Ajoutons que si Christiaan Huygens, en vue de l'application qu'il va faire dans le § IX, s'est borné dans sa conclusion au cas αδΠ = 45o, la phrase de l'anagramme: data harum curvarum quadratura catenae puncta quodlibet invenire possum nous démontre qu'il n'a pas manqué la conclusion plus générale que nous venons de formuler. Pour y arriver, on n'a qu'à changer les derniers mots qui précèdent cette note dans le texte comme il suit: (puta arcus αΠ) ad totidem radios, sit ut spatium δωϰμ ad ▭ αμ.
-
voetnoot22)
- Cette équation est identique avec la seconde de celles qui sont mention nées dans l'anagramme. La quadrature d'ailleurs peut s'effectuer facilement et Huygens n'a pas manqué de s'en apercevoir plus tard, comme on le verra dans la suite de cette correspondance. On a, en effet, pour la courbe δωΘ (fig. 5).
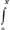 ydx= ydx=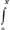 axdx/√aa+xx=a√aa+xx-aa. axdx/√aa+xx=a√aa+xx-aa.
Appliquant ensuite le théorème démontré dans le texte de ce § VII et posant x = a tg ϕ, où ϕ = ∠ αδΠ représente l'angle de la tangente de la chaînette avec la ligne horizontale, on trouve:
AL (fig. 4): arc AK = a√aa + xx - aa∶ax = sec ϕ - 1∶tg ϕ = cosec ϕ - cot ϕ∶1.
Comme on le verra dans la dernière note de cet article, Huygens a fait usage de ce résultat pour corriger la valeur du rapport de l'ordonnée à l'arc de la chaînette pour ϕ = 45o.
-
voetnoot23)
-
Construction de la courbe xxyy = a4 - aayy de l'anagramme, dont la quadrature fait connaitre le rapport de l'abscisse LK (fig. 4) à l'arc AK de la chainette pour un angle donné de la tangente KS avec la ligne horizontale. Le paragraphe est emprunté à la page 61 recto. Plus tard Huygens, comme nous verrons dans la suite de cette correspondance, a su réduire la quadrature de cette courbe au calcul de la somme des sécantes dont les angles croissent par intervalles égaux et petits depuis zéro jusqu'à l'angle ϕ de la tangente KS (fig. 4) avec la ligne horizontale, c'est-à-dire au calcul de l'intégrale
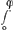 secϕ dϕ. Toutefois, la réduction à la quadrature de l'hyperbole, quoique possible, lui a échappé. secϕ dϕ. Toutefois, la réduction à la quadrature de l'hyperbole, quoique possible, lui a échappé.
-
voetnoot24)
-
Calcul des nombres 10000, 8809, 4134 de l'anagramme, proportionnels à l'arc AK (fig. 4), à l'abscisse LK et à l'ordonnée AL, pour les cas ∠ KTI = 45o. Ce paragraphe est emprunté à la page 61, verso. Plus tard, Huygens y a ajouté la suscription: Dimensio p. approxim spatii αθζδ pag. praec. nam spatium δθζ quadrabile est.
-
voetnoot25)
- La première de ces colonnes contient les tangentes croissantes par intervalles égaux depuis zéro jusqu'à la valeur de la tangente de 45o; la valeur du rayon étant supposée égale à 10000. La seconde contient les sinus et la dernière les cosinus correspondants. Les divisions par 2, que l'on rencontre en haut et en bas de ces colonnes, s'expliquent par l'emploi de la formule approximative
(½ y0 + y1 + y2 +...+ ½ y8) × Δ
que l'on obtient en remplaçant l'aire d'une courbe par une somme de trapèzes. Dans la colonne des sinus y0 = 0, dans celle des cosinus y0 = 100000. Le nombre 800000 représente la somme des rayons.
L'approximation obtenue de cette manière est assez grossière. Aussi Huygens ne s'en est pas contenté, comme la note suivante le montrera.
-
voetnoot26)
- Plus tard Huygens ajouta la remarque: ‘Haec melius page 90 et 91. Hic nimis pauca rectangula 8 cum illic sint 40 et aptiori methodo inventa’. En effet, aux pages citées, c'est-à-dire aux pages 95 recto et verso de la pagination générale du livre G, on rencontre un calcul, dans lequel le nombre des divisions est porté de 8 à 40. De plus, ce calcul se fonde sur l'emploi de l'équation y = a2/√a2 + x2 de la courbe en question, dont les ordonnées successives sont calculées au moyen de logarithmes à sept décimales. De cette manière, le nombre 88135, 5 est obtenu, dont toutefois Huygens ne s'est pas encore contenté, ainsi qu'il résulte du petit calcul suivant, qui a fourni le nombre 88137 mentionné dans la note 6 de la pièce No. 2624 et par lequel Huygens remplaça le nombre 88091 du texte.
Voici ce calcul:
| ex 5 |
880156 |
|
|
diff.ae 0904 |
|
| ex 10 |
881060 |
|
230 videntur fere quadruplae sequentium. |
| ex 20 |
881290 |
065 |
|
| ex 40 |
881355 |
|
|
16 |
add. ¼ 65 |
|
|
881371. |
Haec ergo erit accuratior magnitudo spatii BϕDA pag. 88 (δαψθζ de la figure 5). | |
|