Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 189]

N^o 2182.
De Vaumesle à Christiaan Huygens.
31 Juillet 1679.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre fait suite au No. 2149.

Monsieur

Je vous enuoye enfin les demonstrations geometriques²⁾ dont Je vous parlé il y a huit ou neuf mois dans la lettre que Jeus lhonneur de vous ecrire en cetemps la. elles ne sont pas autant correctes quelles deuvoient estre pour paroistre a paris mais la honte que Jauois destre si long temps a vous enuoyer si peu de chose a fait que Je né pu me resoudre a tarder dauantage a vous les enuoyer me reseruant neanmoins (si elles ont le bonheur dauoir votre approbation et celle des autres mrs. de lacademie qui les pourront voir si vous les en jugez dignes) de les mettre en meilleur estat et selon les defauts que vous y remarquerez. car quoy quelles fussent au point que Je ny pusse remarquer aucune faute Je croy que vous y en trouuriez encor cest pourquoy Jay mieux aimé vous les enuoyer en lestat quelles sont qui est tel que vous les entendrez assez bien pour en juger et mendire votre sentiment que d'attendre dauantage a vous les enuoyer plus correctes a la verité mais ou il y auroit encor eu a corriger vne seconde fois.

Jay mis les figures apart pour la commodité²⁾ de ceux qui liront ces demonstrations car quand la figure dvne proposition est sur la page d'vn feillet et la demonstration sur lautre cest vne incommodité destre obligé de tourner le feillet bien des fois.

puis quil me reste encor du papier vous ne serez pas fasché que Je vous entretienne encor vn peu et que Je vous die quelque chose de notre cycloide circulaire³⁾ en la quelle Je trouue certainnes proprietez qui peuuent, ce semble contribuer a la mesure du cercle car ca esté la consideration de cette ligne courbe qui ma fait trouuer sans que Jy pensasse la quadrature du cercle par latouchement de la spirale que vous voyez a la fin des autres⁴⁾. ce Je veux vous dire a present est que si il y a vne suitte de polygones inscris en vn mesme cercle comme il est dit au commencement de la premiere proposition des demonstrations que Je vous enuoye

1) Au Fasciculus II de l'ouvrage cité dans la Lettre N^o. 2057, note 2.

2) Malheureusement ces démonstrations avec les figures, qui ont accompagné cette lettre, nous manquent.

2) Malheureusement ces démonstrations avec les figures, qui ont accompagné cette lettre, nous manquent.

3) La cycloïde circulaire est mieux connue aujourd'hui sous le nom de cardioïde.

4) Voir, sur cette même quadrature, la Lettre N^o. 2145.

[p. 190]

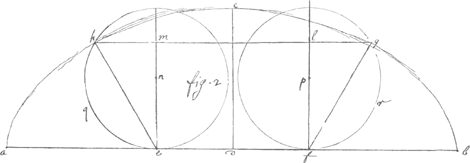
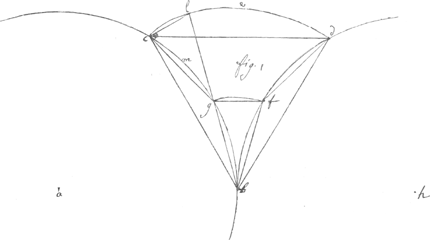
et que ces polygones ayent beaucoup de costez par exemple le premier a 90 costez le second 180 le 3^e 360 etc. Je dis que la difference du cercle et du polygone de 180 costez nest guere que letiers de la difference des polygones de 180 et 90 costez tout de mesme que la difference du cercle et du polygone de 360 costez nest guere que le tiers de la difference des polygones de 360 et 180 costez et ainsij de tous les autres ce que Je prouue ainsij le cercle a b g c⁵⁾ est la base ou cercle immobile dvne cycloïde circulaire dont le point c est le commencement h b f d est le cercle mobille ces deux cercles se touchent au point b les arcs b g c et b f d sont tous deux de 60 degrez c l e d est larc de la cycloide decrit par la reuolution de larc b f d sur c g b. lespace compris de la ligne droitte b d des arcs d e l c et c g b est quintuple de lun des segments de cercle b g c ou b f d si a cet espace on adioute le segment c g b lespace b d e l c est sextuple du segment c g b cet espace donc auec lexagone inscript au cercle a b g c est egal a ce mesme cercle.

Si on ne prend a present que le petit arc c l de la mesme cycloïde qui est decrit par la reuolution de larc f d sur larc c g qui sont les moittiez des arcs b g c et b f d par la mesme demonstration que dessus lespace g c l est sextuple du petit segment de cercle c m g le double de lespace g c l est donc egal a 12 fois le segment c m g le double de cet espace auec le dodecagone inscript au cercle a b g c est donc egal a ce mesme cercle. mais parce que les triangles g c l et c g b sont egaux le double du triangle g c l est le tiers de six fois le triangle c g b et six fois le triangle c g b est la difference du dodecagone et de lexagone inscrit au cercle a b g c donc deux fois le triangle g c l est egal au tiers de la difference des dodecagone et exagone susdits et le double de ce triangle g c l est presque egal a la difference du cercle a b g c et du dodecagone inscript en iceluy car il ne sen faut que deux fois le petit segment c l de la cycloide et ces petits segments diminuant tousiours il est evident que quand les polygones auront beaucoup de costez que la difference du cercle et d'un polygone nest guere que le tiers de la difference de ce polygone et de lautre polygone inscript au mesme cercle et qui n'a que la moittié des costez du premier.

Il me reste encor assez de papier pour vous dire encor comment on peut inferer d'vne des demonstrations que Je vous enuoye ce que vous auez trouué le premier dont Je né pas vu la demonstration qui est que la portion de lespace de la cycloïde ordinaire retranchéé par une ligne parallelle a la base qui passe par le point de laxe eloigné du sommet du quart de laxe est egal au triangle equilat. ou a la moitté de lexagone inscript au cercle generateur⁶⁾ voyez la 2 fig. a b est vne ligne droitte diuiséé en deux parties egalles au point d egalle a la circonfer. du cercle dont le

5) Voir la figure 1, de la planche vis-à-vis de cette page.

6) Voir la Lettre N^o. 503. Il s'agit ici d'une quadrature absolue (indépendante de celle du cercle) d'une partie de la cycloïde, et qui aurait été remarquée pour la première fois par Huygens. Consultez la Lettre N^o. 566.

[p. *3]

[p. 191]

diametre est d c perpendicul. a a b. les lignes a e e f et f b sont egalles. les cercles egaux n e q h et p f r g touchent la ligne a b en des points e et f et leurs diametres sont egaux a d c. les arcs e q h et f r g sont chaquun le tiers de toute la circonf. les points h et g sont donc deux points de la cycloïde ordinaire. Il est certain que le rectangle e m l f est egal au cercle generateur, que le triangle e h m est la moittié du triangle equilateral inscript au cercle. le trapese e h g f est donc egal au cercle generateur et au triangle equilateral inscript en iceluy et que suiuant ce que Jay demonstré que lespace compris des lignes droittes e h et e b⁷⁾ et de larc de la cycloide a h est egal a trois fois le segment de cercle e g h qui adioutez au triangle equilateral sont egaux au cercle generateur. cet espace donc adiouté qu trapese e h g f est egal a deux fois le cercle generateur. et puisque lespace entier compris de toute la cycloide et de sa base est egal a trois fois le cercle generateur les deux espaces restans dont vn est celuy qui est compris de la ligne h b⁸⁾ et de larc de la cycloide h c g et lautre est compris des lignes f b et f g et de larc g b de la cijcloide sont donc tous deux ensemble egaux au cercle generateur mais lespace compris des lignes droittes f b et f g et de larc g b de la cycloide est egal a trois fois le segment f r g donc lautre espace est egal au triangle equilateral inscript au cercle generateur puis que trois fois le segment f r g et et le triangle equilateral sont egaux au cercle. Je finis monsieur et vous prie dexcuser de ceste trop longue lettre de m'honorer dun petit mot de response et de croire que Je suis auec bien du respect

Monsieur

Vostre tres humble et tres obeissant serviteur De Vaumesle.

a hambije ce 31 juillet 1679.

A Monsieur

Monsieur Huguens a Paris.

7) Lisez: e a.

8) Lisez: h g.