Oeuvres complètes. Tome IX. Correspondance 1685-1690

N^o 2612.
Christiaan Huygens.
[1690].
Appendice au No. 2611¹⁾.

La pièce se trouve à Leiden, coll. Huygens.

1) Voir la note 10 de la lettre précédente.

I.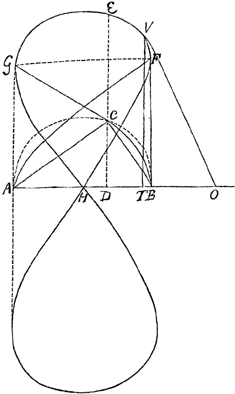

ACB est semicirculus. GEF curva ejusmodi ut semper ED perp. AB sit aequalis duabus AC, CB (vel earum differentiae)²⁾, hujus aequatio (posita HA = a, HD = x, DE = y) est √2aa + 2ax + √2aa - 2ax = y 4aa + 2√.√. = yy 2√.√. = yy - 4aa y⁴ - 8aayy + 16aaxx = 0 VO tangens. Ergo ex regula TO = = 4y⁴ - 16aayy / 32aax³⁾ subt. sive y⁴ - 4aayy / 8aaxsedy⁴ = 8aayy - 16aaxx. Ergo TO = 4aayy - 16aaxx/8aax sive yy - 4xx / 2x sive yy/2x - 2x. Hinc Leibnitio curvae naturam inquirendam proposui in epistola d. 24 Aug. 1690.

2) Les mots entre parenthèses ont été ajoutés plus tard, comme une inspection minutieuse du manuscrit le démontre; il en est de même de la partie de la courbe qui dans la figure correspond à la différence, en opposition à la somme, des lignes AC et CB. Ainsi cette figure ne montra primitivement que la partie qui se trouve au-dessus de la ligne GF et la partie inférieure correspondante. Consultez la lettre de Huygens à Leibniz du 19 décembre 1690 et l'Appendice de cette dernière lettre.

3) Dans cette expression et dans celles qui vont suivre nous avons reproduit les signes des termes tels qu'ils avaient été écrits primitivement. La règle, appliquée par Huygens, est celle même qu'il avait formulée en 1663 dans la Lettre N^o. 1101 et qui fut publiée plus tard dans l'ouvrage cité dans la Lettre N^o. 1912, note 7, et les signes avaient été choisis en conformité avec elle. Dans le cas de la figure où le point O se trouve à droite du point T, elle mène à une valeur positive de la soustangente; dans le cas contraire à une valeur négative. Cette circonstance est mentionnée expressément dans l'exposé de la règle qui, sous ce rapport aussi, ne laisse rien à désirer en précision et en clarté.
Plus tard Huygens, par suite d'un malentendu entre Leibniz et lui sur le signe de la soustangente, sur lequel nous reviendrons à l'occasion de la lettre de Leibniz à Huygens du 13 octobre 1690, a changé partout dans les numérateurs les signes des termes et ajouté la phrase (biffée depuis) ‘sed TO = -yy/2x + 2x = subtangens sic debebam proponere Leibnitio’.

[p. 474]

Spatium AGEFB compositum est ex duabus semiparabolis AFB, BGA, ideoque = 4/3 qu. AGFB unde spat. GEF = ⅓ qu. ejusdem.

II.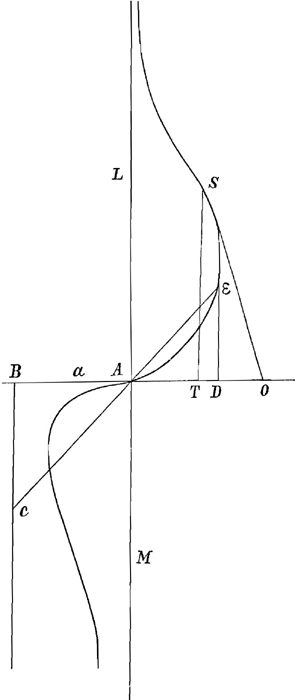

BC parallela AL et perpend. in AB. Curvae AE proprietas est ut, datâ EAC, quadratum AE sit aequale rectangulo ex AB, BC.

[p. 475]

x - y - a | ay/x

aay/x = xx + yy

aay = x³ + xyy

0 = xyy - aay + x³ aequatio curvae.

SO tangens. Ex regula 2xyy - aay / yy + 3xx⁴⁾

xx = aay/x - yy

2xyy - aay / yy + 3aay/x - 3yy | 2xyy - aay / 3aay/x - 2yy | 2xxy - aax / 3aa - 2xy OT.

Hinc curvam inveniendam proposui Leibnitio 24 Aug. 1690⁵⁾.

Si x sit cum signo -, debebit et y esse cum signo -, unde liquet curvam EA descendere sub rectam DAB, et ad alteram partem rectae LAM. Rectang. AT, TS = xy semper minus erit qu.^o AB, sed quamlibet prope accedit minuendo x.

4) Ici encore Huygens a changé plus tard les signes des numérateurs.

5) Plus tard Huygens, après avoir apporté les changements indiqués, ajouta encore la phrase (qu'il n'a pas biffée cette fois): ‘Sed male scripseram OT 2xxy - aax / 3aa - 2xy inversis signis in numeratore’.