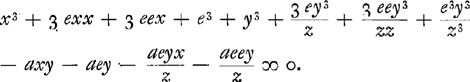Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 312]

N^o 1101.
Christiaan Huygens à J. de Witt.
[25 février 1663].
Appendice au No. 1100.

La minute et la copie se trouvent à Leiden, coll. Huygens.

Inventio Methodi ad Tangentes Linearum Curvarum.

Sit data curva quaelibet geometrica ABC quae cognitam relationem habeat ad rectam aliquam AF, in qua datum punctum A. Ac proinde applicatâ è puncto curvae aliquo ut B, rectâ BF in dato angulo BFA, certa aequatione relatio quae est inter AF et FB expressa habeatur. Si igitur ad datum in ea punctum velut B tangens sit ducenda, concipienda primo est recta EBD quae curvam secans in puncto B itemque in alio ipsi proximo D, occurrat rectae AF in E, et ab utrisque punctis B, D, ordinatim ad AF applicandae BF, DG.

Vocentur jam datae lineae AF, x; FB, y. ponaturque etiam FG data esse quae vocetur e. quaeraturque FE quae dicatur z. Itaque sicut EF, ad FB hoc est sicut z ad y ita EG hoc est z + e ad GD quae erit y + ey/z. Et hoc quidem in qualibet curva perinde se habere liquet.

Nunc porro consideretur aequatio naturam curvae continens exempli gratia x³ + y³ - xya ∞ o ubi a datam longitudinem rectam significet AH. et patet, quum punctum D in curva ponatur, debere eodem modo duas AG, GD, hoc est x + e et y + ey/z ad se mutuo referri atque AF, FB, hoc est x et y. Itaque si in aequatione proposita substituatur ubique x + e pro x et y + ey/z pro y, debebit esse

In hac autem aequatione constat necessario terminos prioris aequationis simplicis reperiri debere, nempe x³ + y³ - axy, qui cum sint aequales nihilo ex proprietate curvae, idcirco his in aequatione deletis, necesse est residuos etiam aequari nihilo; in quorum singulis manifestum quoque est vel unum e vel plura reperiri,

[p. 313]

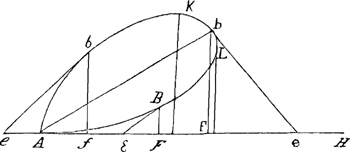
ideoque omnes per e dividi posse. qui autem post hanc divisionem non amplius habebunt e, eos, neglectis reliquis, scio nihilo aequari debere quantitatem que lineae FE sive z ostensuros, si nempe BE jam tanquam tangens consideretur, ideoque FG sive e infinitè parva. nam termini in quibus adhuc e superest etiam quantitates infinite parvas sive omnino evanescentes continebunt. Video ìtaque ex aequatione tota tantum eos terminos scribi necesse esse quibus inest e simplex, velut hic 3 exx + 3ey³/z - aey - aeyx/z ∞ o. Qui termini quomodo facili negotio ex datis aequationis terminis x³ + y³ - axy ∞ o describi possint deinceps explicandum.

Et primo quidem apparet 3 exx + 3ey³/z nihil aliud esse quam secundos terminos cuborum ab x + e et ab y + ey/z, ideo scriptos quia in aequatione habentur cubi ab x + e et y. Nam reliqui omnes termini cuborum ut et quarumvis aliarum potestatum ab x + e et ab y + ey/z, vel plura quam unum e habent, vel nullum; ideoque, ut jam diximus, frustra scriberentur. Eadem igitur ratione, si aliae potestates ab x vel y essent in aequatione proposita, scribendi forent in aequatione altera termini secundi tantum similium potestatum ab x + e et ab y + ey/z. Notandumque secundos hosce terminos ex ipsis datis potestatibus x et y certa ratione confici; nempe ex potestate quavis x veluti x³, mutando unum x in e et praeponendo numerum dimensionum ipsius x; ita hic fit 3 exx. Ex potestate y vero, ducendo eam in e/z, praeponendoque similiter numerum dimensionum ipsius y; ita hic ab y³ fit 3y³e/z. Quorum quidem rationem ex potestatum formatione intelligere facillimum est.

Porro propter xy in termino aequationis - axy, facile quoque apparet quid in aequatione secunda scribendum sit. cum enim substituendum sit pro xy productum ab x + e in y + ey/z, sed ea tantum scribenda in quibus unum e, ideo de duobus x + e tantum e ducemus in y, et tantum x in ey/z, adeoque fient ey + ey/z¹⁾, quibus in a ductis, praepositoque signo -, quia habetur - axy, existet - aey - aexy/z, sicut supra.

1) Lisez: exy/z.

[p. 314]

Sic quoque, si exempli gratia in aequatione proposita habeatur xxy³; sumam, propter xx, duos priores terminos quadrati ab x + e, nempe xx + 2 ex; et, propter y³, duos priores terminos cubi ab y + ey/z, nempe y³ + 3ey³/z: quorum productum pro xxy³ surrogandum. Sed etiam hic, de duobus xx + 2 ex, tantum xx ducendum in 3ey³/z, tantumque 2 ex in y³, (quia caetera plura quam unum e vel nullum haberent) adeo ut fiat 3exxy³/z + 2exy³.

Atque ex his animadvertere licet, semper utrumque horum terminorum describi posse ex dato termino, qui hic xxy³, alterum quidem mutato uno x in e, et praeponendo numerum dimensionum ipsius x; ita enim fit 2 exy³; alterum vero ducendo datum terminum in e/z praeponendoque similiter numerum dimensionum ipsius y; ita enim fit 3exxy³/z. Cumque hac eadem immutatione, paulo ante, etiam secundos terminos potestatum ab x + e et ab y + ey/z, ex potestatibus x et y aequationis datae describi ostensum sit; manifestum jam est, à singulis terminis aequationis datae in quibus x vel potestas ejus, describi praedicta methodo, in secunda aequatione, totidem terminos in quibus non est z. A singulis vero in quibus y vel potestas ejus, describi totidem terminos, dicta etiam methodo, quorum fractionis denominator sit z, nec alibi hanc literam in secunda aequatione repertum iri.

Hoc igitur cognito, quo pacto ex aequatione quavis proposita, velut hic x³ + y³ - axy ∞ o alia describenda sit, ut hic 3 exx + 3ey³/z - aey - aeyx/z ∞ o, animadverto porro, si termini divisi per z ad alteram partem aequationis transferantur, ductisque omnibus in z, dividantur per reliquos terminos in quibus non est z, existere tunc ipsam quantitatem z ∞ - 3 ey³ + aeyx / 3 exx - aey. atque hinc intelligo ad consequendam quantitatem z, ponendos tantum eos terminos aequationis secundae qui descripti sunt ex terminis aequationis primae in quibus y, sublato tantum denominatore z, mutatisque signis + et -. deinde dividendos istos terminos per eos qui descripti sunt ex terminis aequationis primae, in quibus x. Porro ex omnibus tam divisis quam dividentibus patet rejici posse e, adeo ut in hoc exemplo fiat z ∞ - 3 y³ + ayx / 3 xx - ay. Itaque rejicitur e/z ex terminis qui descripti sunt ab ijs qui habent y. Ita autem descriptos eos superius diximus ut ducerentur in idem e/z, praeponereturque numerus dimensionum y. Ergo nihil requiri ap-

[p. 315]

paret ad terminos hosce, (quatenus ad definiendam quantitatem z hic adhibentur,) ex terminis aequationis primae, in quibus y, describendos, quam ut praeponamus tantum ijs numerum dimensionum quas in ipsis habet y, signaque + et - invertamus. Sic nempe ab y³ - axy describetur - 3y³ + axy. A terminis vero qui descripti sunt à terminis aequationis primae quibus x, cum tantum e hic rejiciendum patuerit; cumque hos ita prius descriptos dixerimus, ut unum x mutaretur in e, praeponereturque numerus dimensionum ipsius x; apparet eos quatenus hic ad constituendum divisorem adhibentur, sic tantum describi opus esse ex terminis propositae aequationis in quibus x, ut praeponatur ijs numerus dimensionum ipsius x, ac deinde unum x auferatur. Sic nempe ab x³ - axy describetur 3 x³ - axy; et dempto ubique x uno, fiet 3 xx - ay.

Hinc itaque compendiosa regula oritur ad curvae cujusvis tangentem inveniendam, ex data solummodo aequatione quae proprietatem ejus explicet, et in qua x et y significent eas quas a principio ijs attribuimus lineas datas.

Regula.

Translatis enim terminis omnibus aequationis datae ad unam aequationis partem, qui proinde aequales siunt nihilo, multiplicentur primo termini singuli in quibus reperitur y, per numerum dimensionum quas in ipsis habet y: atque ea erit quantitas dividenda. Deinde similiter termini singuli in quibus x, multiplicentur per numerum dimensionum quas in ipsis habet x et e singulis unum x tollatur; atque haec quantitas pro divisore erit subscribenda quantitati dividendae jam inventae; quo facto habebitur quantitas aequalis z sive FE, a cujus termino E ducetur quae tangat curvam in dato puncto B. Ne autem signa ulla + et - immutare opus sit, sciendum tantum, licet quantitas divisoris, vel dividenda vel utraque, minor nihilo sive negata inveniatur, tamen tanquam affirmatas esse considerandas; hoc tamen observando ut cum altera affirmata est altera negata, tunc z sive FE sumatur versus punctum A; cum vero utraque vel affirmata vel negata est, ut tunc sumatur FE in partem contrariam.

Exempli gratia in curva modo proposita, cum aequatio ejus sit x³ + y³ - axy ∞ o, fiet dividenda quantitas, secundum regulam, 3 y³ - axy; divisor vero 3 xx - ay; Ideoque z ∞ 3 y³ - axy / 3 xx - ay. Evenietque in hac curva, ut si punctum b²⁾ ad quod tangens ducenda est, detur inter puncta K et L, quorum tangentes, altera lineae AF parallela est, altera perpendicularis; eveniet inquam tunc, ut divisore 3 xx - - ay minore existente quam nihil, etiam dividenda quantitas 3 y³ - axy, minor sit nihilo, et contra cum ille major nihilo, etiam haec major sit, sive adfirmatam

2) Consultez la figure de la page suivante.

[p. 316]

quantitatem continens; ac proinde tunc fe non versus A sed in alteram partem sumendam liquet. In alijs vero curvae partibus si punctum detur ut B vel b, semper eveniet altera quantitate negata existente, alteram esse adfirmatam, et contra. unde tunc apparet sumendam FE versus A.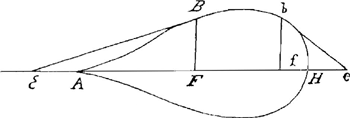

Esto rursus curva ABH, cujus aequatio axx - x³ - qqy ∞ o. Posito scilicet a et q esse lineas datas. AF vero ∞ x; FB ∞ y; FE ∞ z. Hic fiet, secundum regulam, dividenda quantitas - qqy: divisor 2 ax - 3 xx; unde z ∞ - qqy / 2 ax - 3 xx. Ubi, cum dividenda quantitas sit negata, si fuerit etiam divisor minor nihilo, hoc est, si 2 a minor quam 3 x; erit z sive fe sumenda in partem aversam ab A. Si vero 2 a major quam 3 x, sumenda erit FE versus A ex praecepto regulae.

Unde vero comperta sit differentia illa, ut intelligatur, repetenda est figura in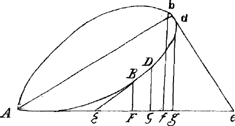



principio horum posita, ubi vidimus AG esse x + e. EG vero z + e, unde fiebat GD ∞ y + ey/z. Si autem tangens ab altera parte lineae BF cadere concipiatur velut b e, atque haec curvam secare fingatur ut ibi factum est, in d. fiet ponendo rursus f g ∞ e et f e ∞ z ut AG³⁾ quidem fiat x + e. sed eg erit

3) Lisez: Ag.

[p. 317]

z - e, unde erit g d ∞ y - ey / z. Atque hinc porro facile est perspicere aequationem secundam quae ex proposita aequatione exscribitur, hoc casu fore 3 exx - 3 ey³ / z - aey + aeyx/z ∞ o, ut nempe termini qui per z dividuntur habeant signa contraria ijs quae habebant in aequatione descripta casu priori quae erat 3 exx + 3 ey³ / z - aey - aeyx/z ∞ o. Ex hac vero sequitur, quando quantitas 3exx - aey sive quando 3 xx - ay, (quae divisorem constituit, secundum regulam) fuerit minor nihilo, sive negata, tunc quantitatem reliquam 3 ey³ / z - aeyx / z sive etiam 3 y³ - ayx (quae quantitatem dividendam secundum regulam constituit) esse affirmatam; aut cum illa est affirmata hanc esse negatam; quia omnes simul aequationis termini aequantur nihilo. At contra ex illa aequatione 3 exx - 3 ey³ / z - aey + aeyx / z ∞ o sequitur quando quantitas 3 exx - aey sive quando 3 xx - ay fuerit negata, tunc reliquam - 3 ey³ / z + aeyx / z sive etiam - 3 y³ + ayx esse affirmatam, sive quod idem est, 3 y³ - ayx esse negatam: aut quando 3 xx - ay fuerit affirmata, tunc - 3 y³ + ayx esse negatam, sive quod idem est 3 y³ - ayx esse affirmatam. Per haec itaque apparet ex quantitatibus per regulam inventis, quae erant 3 y³ - ayx / 3 xx - ay ∞ z judicari posse ad utrum casum constructio tangentis pertineat, nempe, ex comperta dissimilitudine affectionis in divisore et dividendo, sequi ad priorem casum eam pertinere, hoc est, z sive FE accipiendam esse versus A. Ex similitudine vero eorum affectionis, sequi ad contrariam partem sumendam.