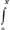Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 546]

N^o 2636.
G.W. Leibniz à Christiaan Huygens.
24 novembre 1690.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et par C.I. Gerhard²⁾.
La lettre est la réponse au No. 2633.
Chr. Huygens y répondit par le No. 2643.

A Hanover ce 14/24 de Novembre 1690.

Monsieur

Je reponds incontinent à la vostre du 18 de Novembre, afin que vous ne me soubçonnies pas d'une vanité ridicule, comme si j'auois crû, que ce que j'auois dit dans les Actes de Leipzig vous auoit servi pour vostre series 1/1a + ⅓a³ + ⅕a⁵ etc. Vous estes trop sincere pour dissimuler l'usage que vous faites des pensées des autres, et vous avés marqué en cela même, que celles de Mr. Neuton vous avoient servi. J'auois dit seulement qu'il y a de l'accord, et cela est ainsi, car je dis en termes expres article 5 n^o 3, resistentias esse in ratione composita elementorum temporis et quadratarum velocitatum. De sorte que les elements du temps estant pris egaux, comme on les prend ordinairement, les resistences sont en raison doublée des vitesses; et cela s'ensuit de ce que j'auois dit que les resistences sont en raison composée des vitesses et des elemens de l'espace. Car les elemens de l'espace sont en raison composée des elemens du temps et des velocités. En symboles, soit resistence r, vitesse v, temps t, espace s, leur elemens dv, dt, ds, il est tousjours vray que ds sont comme dt. v et icy r est comme ds. v, donc r comme dt. vv. Et quoique les resistences dependent de la vitesse, comme vous dites, elles dependent aussi de la quantité des parties du milieu qui resiste. Un globe en mouuement rencontrant un globule en repos, la perte, qu'il fait de sa velocité est proportionnelle à la velocité (les grandeurs des globes et tout le reste demeurant, hors mis la velocité) comme il est aisé de demonstrer. Mais plus il rencontre des globules, et plus grande est sa perte; or le milieu estant uniforme, le nombre des globules sera comme les parties de l'espace. Mais a fin que vous jugies mieux de cet accord, je dis, que j'ay precisement determiné le même rapport entre les temps et les velocités. Il est vray qu'il y a eu une trajection ou transposition³⁾ dans l'edition, qui est de ma

1) Chr. Hugenii Exercitationes Mathematicae etc. Fasc. I, page 44.

2) Leibnizens Mathematische Schriften, Bd. II, p. 59 et Briefwechsel, p. 617.

3) En réalité, il n'en est pas ainsi. Les propositions 4 et 6 sont parfaitement correctes telles qu'elles étaient formulées dans l'article cité et que nous les avons reproduites dans la note 10 de la Lettre N^o. 2632. Leibniz s'en est aperçu plus tard. Aussi, dans sa lettre à Huygens du 5 décembre, notre N^o. 2639, il a rétracté les corrections qu'il propose ici.

[p. 547]

faute, mais j'estois en voyage et bien distrait. En voicy la correction. C'est qu'il faut mettre les espaces pour les temps et vice versa dans les propositions 4 et 6 de l'article 5, et apres auoir ainsi corrigé les propositions, il faut donner la demonstration de l'une à l'autre, et vice versa. De sorte voicy comme il falloit dire dans la prop. 4 en y mettant la prop. 6 corrigée: si velocitates acquisitae sunt ut sinus erunt tempora impensa ut logarithmi sinuum complementi, posito radium seu sinum totum esse ut velocitatem maximam. Et à cela s'ajuste la demonstration qui est mise a la proposition 4^me, cum enim (j'en repete les paroles) incrementum velocitatis sit differentia inter impressionem et resistentiam, hinc ex proecedenti statim sequitur impressionem (gravitatis) esse ad incrementum velocitatis, ut quadr atum velocitatis maximae ad excessum hujus quadrati super quadratum proesentis velocitatis. Ex quo scimus per quadraturas, summam impressionum quae est proportionalis assumto tempori, esse ut Logarithmum, si numerus sit qualem in propositione hac enuntiavimus. Ce sont mes paroles precises et pour vous faire voir qu'elles s'ajustent à la proposition ainsi corrigée et transposée, aussi bien qu'avec vos decouuertes⁴⁾, Appellons comme auparavant le temps t, les velocités v, la plus grande velocité a, les resistences r. Or il est manifeste que les elemens des velocités c'est à dire les differences de deux velocités prochaines se trouuent en adjoutant à la velocité precedente la nouuelle impression faite par la gravité et en soustrayant en mesme temps la resistence ou perte causée par le milieu, donc dv (increment de la velocité precedente pour faire la suivante) est dt - r⁵⁾, or r = dt.vv/aa donc dv = = dt - dt vv/aa ou bien dt/dv = aa/aa - vv, c'est à dire, comme parle ma demonstration: impressio gravitatis (dt) est ad incrementum velocitatis (dv) ut quadratum velocitatis maximae (aa) ad excessum huius quadrati super quadratum praesentis velocitatis (aa - vv). Car dt expriment aussi bien les elemens des temps, que les impressions de la pesanteur, qui sont proportionnelles à ces elemens. Par là vous voyés, Monsieur, que t = ∫ dv . aa / aa - vv, ou parlant à l'ordinaire, que le temps est la somme de aa/aa - vv, c'est à dire selon vostre expression, que le temps est 1/1v + ⅓v³ + ⅕v⁵⁶⁾

4) Consultez la note 7 de la Lettre N^o. 2632.

5) Cette formule suppose que les unités de temps et d'espace soient choisies d'une telle manière que l'accélération de la gravité soit représentée par l'unité. Le choix singulier ou trop peu precisé des unités employées, dont on rencontrera encore un autre exemple dans cette lettre, tend quelquefois à répandre sur les raisonnements et les résultats de Leibniz, un certain vague qui devait rebuter un esprit aussi exact que celui de Huygens. Celui-ci ne s'en cache pas dans sa réponse à cette partie de la lettre.

6) En réalité, le temps est proportionnel à (v/a) + ⅓(v/a)³ + ⅕(v/a)⁵ +...

[p. 548]

etc. Mais selon la mienne, les temps sont comme les logarithmes de √(aa - vv)⁷⁾ c'est à dire les velocités v estant comme les sinus, les temps sont comme les logarithmes sinuum complementi. Et vous trouverés que ces deux expressions s'accordent. J'auois crû mieux faire en m'exprimant ainsi. En echange la proposition 4^me corrigée (les espaces estant mis pour les temps) doit estre mise à la place de la sixieme et alors la proposition sixieme veritable sonnera ainsi: si rationes inter summam et differéntiam velocitatis maximae et minoris assumtae sunt ut numeri, spatia quibus assumtae velocitates sunt acquisitae, sunt ut logarithmj. Et alors la demonstration de la proposition 6^me repondra à sa proposition. En symboles les espaces estant marqués de s et les elemens de ds comme auparavant, puisque r = = ds . v/a et dt = a/v ds⁸⁾ substituant ces valeurs dans l'equation susdite dv = = dt - r, on aura ds=dv . av / aa - vv ou s = ∫ dv . av / aa - vv. Ce qui depend encorde la quadrature de l'Hyperbole ou des Logarithmes. On le pourroit encor exprimer par cette series s = ½vv + ¼v⁴ + ⅙v⁶ etc. mais j'ay crû mieux faire en disant, que les velocités estant v, les espaces sont comme les logarithmes des raisons de a + v à a - v. Ainsi j'ay ces expressions exponentiales (que vous appellés en riant supertranscendentes) √(1 - vv) comme b^t et 1 - v/1 + v comme b^s, b estant un certain nombre constant. Je ne voy pas pourquoy vous trouvés de l'obfcurité dans ces expressions, car il n'y en scauroit plus auoir que dans les logarithmes ordinaires, qui ne vous scauroient donner aucune peine. Et puisque vous avés adjouté quelque limitation à vostre arrest contre ces sortes de formules, en les rejettant, à moins que je n'y aye remarqué quelque utilité notable, j'acheveray d'instruire le procès, a fin que vous puissiés prononcer une sentence definitive. Je crois donc que dans les lignes qui passent les equations de l'Algebre ordinaire, c'est tout ce qu'on peut souhaitter à leur egard en Analyse, que de les exprimer par ces equations nouuelles. Si on le pouuoit tousjours faire, on connoistroit par là parfaitement la nature de la ligne, on pourroit donner ses tangentes, ses quadratures, extensions, centres et même ses intersections avec une courbe donnée, et resoudre par ce moyen des problemes transcendans determinés, en fin je ne voy rien de possible, qui resteroit à faire apres cela, et le tout ne supposeroit que la construction des logarithmes, outre les constructions de la Geometrie ordinaire. On pourra encor determiner les cas quand certains points demandés se peuvent

7) En réalité, comme les logarithmes de a + v / a - v. Consultez la note 10 de la lettre N^o. 2632.

8) Pour justifier cette formule on doit supposer que l'unité de temps soit choisie égale au temps nécessaire pour parcourir l'unité de l'epace avec la vitesse terminale a.

[p. 549]

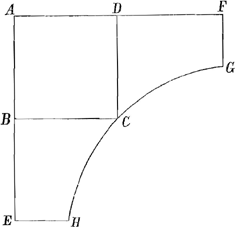
donner par la Geometrie commune. Si ces raisons ne valent rien, je me suis bien trompé de mon calcul. Je croyois vous avoir communiqué quelque chose de fort bon et de grand usage. Et quand j'aurois fait une beveue dans le cas, que je vous avois envoyé, cela ne pourroit rien diminuer de la force de la methode. Par les expressions susdites je donne une equation qui exprime la relation entre l'espace et le temps, car il se trouve 1 - b^s / 1 + b^s = √(1 - b^t). De sorte que les temps estant donnés en nombres, les espaces se trouuent par là et vice versa; en supposant la construction des logarithmes. On aura bien de la peine à arriver icy, par une autre voye, à une equation finie.

Apres avoir examiné la courbe que vous assignés pour la proprieté des Tangentes, et que vous m'aviés proposée, Monsieur, je trouve que vostre courbe semble y repondre, mais qu'elle n'y repond pas de la maniere que la formule est conçue; au lieu que les miennes y repondent. Et il s'y passe quelque chose de curieux à l'égard des signes⁹⁾. Je trouue donc que l'equation estant x³ + xy² = aay, il provient DB = aax - 2xxy / 3aa - 2xy, au lieu que vous m'auiés proposé 2xxy - aax / 3aa - 2xy. Et a sin qu'on ne pense pas que c'est la meme chose, et qu'il faut parler de la façon posterieure, lorsque le point D doit estre pris ad partes oppositas, et non vers A, je reponds que suivant le calcul, il est toujours vray, soit que CD se mene supra ou infra, c'est à dire vers A ou ad partes oppositas, que DB est aax - 2xxy / 3aa - 2xy dans votre courbe, puisque cette valeur s'obtient par un calcul general, et cela prouue seulement, que lorsque cette valeur est une grandeur negative, D doit estre pris non supra (vers A) mais infra B. Et a fin que vous jugiés mieux de la solidité de cette remarque, et que l'Analyse ne scauroit mener à vostre courbe par la propricté que vous aviés proposée, vous trouuerés que les courbes, que j'auois envoyées, satisfont rigoureusement et uniquement a la valeur 2xxy - aax: 3aa - 2xy, et ne scauroient satisfaire à la valeur aax - 2xxy: 3aa - 2xy; car jettant les yeux sur ma derniere lettre¹⁰⁾ vous trouverés cette equation 3dx/x + dy/y = 2xdy + + 2ydx, dont je puis venir à bout. Car la somme de 2xdy + 2ydx est 2xy, mais si la valeur est aax - 2xyy: 3aa - 2xy, vous trouuerés 3dx/x - dy/y = -2xdy + +2ydx. Mais la somme de - 2xdy + 2ydx ne se trouue pas de même, et il faut auoir recours à d'autres adresses, dont je ne m'estois pas servi parce que j'estois devenu fort aisément à ce que vous m'aviés demandé: Apres tout cela, je

9) Consultez la note 3 de la pièce N^o. 2612 et la note 6 de la Lettre N^o. 2627.

10) La Lettre N^o. 2632.

[p. 550]

m'imagine que vostre arrest provisionnel sera addouci, et comme vous devés juger en dernier ressort, et sans appel, vous serés d'autant plus porté à faire droit aux parties.

Je suis bien aise que Mrs. de Leipzig vous ont fait justice dans leurs Actes¹¹⁾; Mais en rapportant la seconde partie de vostre traité il y a une beveue dont je suis fasché. Celui qui a donné cette relation s'est imaginé¹²⁾ que vostre quadrature de l'Hyperbole par 1 + ⅓ + ⅕ + 1/7 etc. estoit la même que celle que j'auois joint à ma Quadrature Arithmetique du cercle, parce que je voyois une certaine analogie assez belle. Cependant la mienne est celle de Mercator, tirée de 1/1 - ½ + ⅓ - ¼ etc., et par consequent differente de la vostre¹³⁾. Je vous asseure

11) Il s'agit des articles des ‘Acta’ d'octobre et de novembre 1690, qui contiennent un exposé assez étendu du Traité de la Lumière et de celui de la Pesanteur.

12) Dans l'article de novembre 1690, cité dans la note précédente, l'auteur de l'exposé du traité de la Pesanteur s'exprimait comme il suit: ‘Hac itaque occasione non solum quadratura hyperbolae per infinitas series profert in medium, quae analoga est quadraturae circuli, quam a celeberrimo Viro G.G. Leibnizio acceptam ad Acta eruditorum 1682, p. 41 sqq., retulimus, imo gemina plane et consentanea illi Arithmeticae Hyperbolae Quadraturae quae dicto in loco proponitur; sed etiam singulares quasdam proprietates lineae Logarithmicae demonstrat.’

13) Dans l'article de 1682, mentionné dans la note précédente, Leibniz avait indiqué l'emploi



de la progression ⅛ + 1/48 + 1/120 + 1/224 + 1/360 etc. pour exprimer l'aire de la figure EBCH, où GCH représente une hyperbole équilatère et AB = BE est supposé = ½. En effet, posant AB = a, BE = x, on a: EBCHE = a²/a + x dx = a²[x/a - ½(x/a)² + ⅓(x/a)³ -..] ou bien, pour x = a = ½:
EBCHE=¼[1 - ½ + ⅓ - ¼ + ⅕ - ⅙ + 1/7 - ⅛ + 1/9 -] = ¼[½ + 1/12 + ⅓0 + + ⅕6 + 1/90 +...] = ⅛ + 1/48 + 1/120 + 1/224 + 1/360 +...
On voit bien que cette progression n'avoit donc rien à faire avec la quadrature de l'hyperbole, proposée par Huygens dans l'Addition au Discours de la cause de la Pesanteur, au lieu cité dans la note 7 de la lettre N^o. 2632.

[p. 551]

que je n'ay aucune part à ce mesentendu, et même je feray en sorte que cela soit remarqué et redressé¹⁴⁾.

Je voudrois pouuoir satisfaire à tous les autres points de vostre lettre, et surtout examiner attentivement ce que j'ay fait sur la figure de la chaine¹⁵⁾, pour faire la comparaison avec vos decouuertes. Mais je suis a present enfoncé dans des vieux papiers et parchemins de nos archives et pressé pour les depecher. Ainsi il me faut prendre du temps pour cela. J'ay demonstration de la regle de la composition des mouuemens, qui me sert de fondement à la decouuerte des tangentes par les foyers¹⁶⁾. Je suis bien aise de scavoir que c'est vous dont M. Fatio entendoit parler¹⁷⁾, pour joindre cette obligation aux autres qu'on vous a. Mons. Spener ne m'a pas ecrit non plus. J'espere qu'il sera plus exact en experiences qu'en correspondences. J'auois eu autre fois la vue d'essayer si par le moyen du vuide on ne pourroit tirer quelque chose des corps, entre autres en y joignant des filtres, puisque ce seroit une espece de presse, plus subtile et plus uniforme que l'ordinaire.

14) Leibniz l'a fait dans son article ‘Quadratura arithmetica communis Sectionum Conicorum quae centrum habent, indeque ducta Trigonometria Canonica ad quantamcunque in numeris exactitudinem a Tabularum necessitate liberata: cum usu speciali ad lineam Rhomborum nauticam, aptatumque illi planisphaerium’, publié dans les Acta d'avril 1691. Après avoir rappelé sa quadrature célèbre du cercle au moyen de la progression 1 - ⅓ + ⅕ - 1/7 +..., il poursuit: ‘Interim insignes quidam Mathematici, quibus veritas primariae nostrae propositionis dudum in his Actis’ (ceux de février 1682) ‘publicatae innotuit, pro humanitate sua nostri qualiscunque inventi candide meminere. Quos inter Ill. Hugenius etiam analogum aliquid in Hyperbola eleganter adjecit, a nostri olim schediasmatis analogia diversum. Ut enim nos dederamus seriem 1/1t - ⅓t³ + ⅕t⁵ etc. per circulum; ita ipse 1/1t + ⅓t³ + ⅕t⁵ etc. per hyperbolam primariam exhiberi notavit’....

15) Voir la Lettre N^o. 2627, note 9.

16) Voir Lettre N^o. 2627.

17) Dans sa réponse à von Tschirnhaus, mentionnée dans la Lettre N^o. 2467, note 2.

[p. 552]

Peut-estre que M. Spener a pensé à quelque chose de semblable avec son siphon qui doit attirer, mais si cela estoit, il ne deuuroit pas avoir manqué. Ainsi je ne scay pas bien ce que c'est. Puis que vous avés fait des experiences de consequence avec l'ambre, je vous diray que feu Mons. Gericke en auoit fait de fort considerables avec des corps electriques. Il m'en ecrivit un jour et j'en chercheray le détail. Ce qui m'a fait croire que la variation de l'eguille a quelque regle (quoiqu'inconnue encor) c'est que j'ay vû des journaux des grands voyages ou elle estoit tres souvent observée et ou elle ne changeoit pas par sauts mais peu à peu.

Comme ma lettre sur les planetes et autres points, que je vous destinois il y a long temps est quasi faite, je la finiray et la mettray au net, pour la vous envoyer aussi tost¹⁸⁾ que je seray un peu plus libre pour pouuoir vaquer à des pensées que je n'ay plus presentes dans l'esprit. Je vous remercie de ce que vous dites de Messieurs Hudde et Witsen. Quoyque je souhaite fort de voir vos pensées punliées, je prefere l'interest de vostre santé à celuy de nostre utilité. Peut-estre pourriés vous donner souuent des pensées detachées qui seroient de consequence sans vous tant attacher à la forme des ouvrages reguliers. Je suis avec tout le zele que je dois

Monsieur

Vostre treshumble et tresobeissant serviteur Leibniz.

A Monsieur Monsieur C. Hugens Seigneur de Zulichem franco Breme

à la Haye.

18) Voir la note 3 de la Lettre N^o. 2632.