Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 9]
| |
No 2659.
| |
[pagina 10]
| |
Si je ne vous honnorois pas autant que je fais, je negligerois une accusation qui n'a pas le moindre fondement. Car je ne voy pas ce qui vous a pû mouvoir à ne pas adjuter foy à une chose de fait dont je vous avois asseuré. Mais vous estimant autant que je dois, je suis bien aise de vous desabuser. J'ay une lettre de Mons. MenckenGa naar voetnoot5) Professeur de Leipzig, qui a soin des Actes, datée du 28 d'Octobre vieux stile, lors que leur Mois de Novembre éstoit déja imprimé (car il paroist le premier jour du mois) ou il me mande (sur ce que je luy avois écrit a l'occasion de vôtre lettre, ou vous vous étonniés de leur silence) que j'en trouverois une relation convenable dans les mois d'Octobre et de Novembre (von des Herrn Hugenii Buch wird mHerr in den October und November Actorum gebührende relation finden), il adjoute que cette fois leur Novembre avoit esté achevé trois semaines plus tost qu'à l'ordinaire. Si vous en desirés voir l'original, je le vous envoyeray. Peut-estre que la veue de ce mois vous aura déja detrompé, et vous aurés remarqué aisément que ce qu'on y dit du consentement de vostre series avec celle que j'avois donnée il y a plusieurs années estant manifestement erronnée, ne pouvoit estre attendu de moy. Je feray temoigner le contraire comme je vous l'ay promis. Mais tout ce proces importe bien peu. Car vous ou moy nous n'avions qu'a voir l'équation de la courbeGa naar voetnoot6) pour connoistre la series, et vous ne l'aviés reduit à l'Hyperbole, que sur la demonstration de Mons. NeutonGa naar voetnoot7), au lieu que je l'avois fait immediatement et avois preferé l'expression par les logarithmes. Mais je n'ay garde de m'imaginer que ce que j'en avois dit vous y ait servi. Je n'avois pas pensé | |
[pagina 11]
| |
pour cette fois à la tangente; ny eu recours à mon theoreme general marqué dans une de mes precedentes, n'ayant eu en vue qu'une expression degagée de toute consideration de la figure, que les logarithmes me fournissoient la plus analytique que je pouvois souhaiter. C'est pourquoy je ne comprends pas comment vous dites de ne pas voir que ma progression v+⅓v3+⅕v5 etc. réponde à la vôtre, parce que, dites vous, je ne me sers pas de la tangente et du secteur hyperbolique. Mais qu'ay je besoin de penser à cette tangente et à ce secteur? N'est ce pas assés, que je donne moyen d'exprimer la quadrature de la figure dont l'ordonnée est 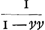 , c'est à dire d'exprimer la grandeur de la series v+⅓v3+⅕v5 etc.=t par les logarithmes, disant que v estant les velocites, les temps t sont comme les logarithmes de , c'est à dire d'exprimer la grandeur de la series v+⅓v3+⅕v5 etc.=t par les logarithmes, disant que v estant les velocites, les temps t sont comme les logarithmes de 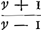 , et vous trouverés tousjours que ∫dv/1-vv ou v+⅓v3+⅕v5 etc. repond au logarithme de , et vous trouverés tousjours que ∫dv/1-vv ou v+⅓v3+⅕v5 etc. repond au logarithme de 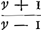 ; c'est à dire les ; c'est à dire les 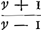 estant pris en progression Geometrique, les grandeurs égales à v+⅓v3+⅕v5 etc. seront en progression Arithmetique. C'est ce que j'avois
dit artic. 5. n. 4. Si rationes inter (v+1 et v-1) summam et differentiam velocitatis maximae (unitatis) et minoris assumtae (v) sunt ut numeri, tempora fore ut logarithmos.
Or je suppose qu'on sçache que la construction des Logarithmes revient à la quadrature de l'Hyperbole. Nous avions tous deux besoin pour un même dessein (c'est à dire pour donner la relation entre les temps et les velocités) de la quadrature de la figure dont l'ordonnée est estant pris en progression Geometrique, les grandeurs égales à v+⅓v3+⅕v5 etc. seront en progression Arithmetique. C'est ce que j'avois
dit artic. 5. n. 4. Si rationes inter (v+1 et v-1) summam et differentiam velocitatis maximae (unitatis) et minoris assumtae (v) sunt ut numeri, tempora fore ut logarithmos.
Or je suppose qu'on sçache que la construction des Logarithmes revient à la quadrature de l'Hyperbole. Nous avions tous deux besoin pour un même dessein (c'est à dire pour donner la relation entre les temps et les velocités) de la quadrature de la figure dont l'ordonnée est 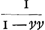 , l'abscisse estant v. Vous l'avés donnée par la series, et moy ne pouvant pas ignorer cette series, j'ay crû mieux faire en la donnant par les logarithmes. Je croyois m'estre expliqué d'une maniere dans la derniere lettre à n'avoir plus laissé d'obscurité. Et pour ce qui est de la correction reïterée, ce n'est que la retractation de la correction, c'est à dire la restitution du premier estat. Car en refaisant le calcul pour vous satisfaire, un abus dans les signes me fit croire que j'avois fait un echange des temps pour les espaces dans les prop. 4 et 6 de l'Article 5. mais depuis j'ay vû qu'il n'y avoit rien à changer comme je vous ay déja mandé. Et lors que vous dites, que s'il est vray que j'aye consideré les resistances de l'air comme en proportion doublée des velocités il faudroit au moins changer l'inscription de l'article 5me, en mettant in proportione quadrata velocitatis, je réponds que si vous aviés consideré ce que je vous avois écritGa naar voetnoot8), vous auriés vû qu'il n'y a rien à changer et je n'aurois pas besoin de repetition mais j'avouë de n'avoir point de droit de vous demander de l'attention. Je dis encor une fois , l'abscisse estant v. Vous l'avés donnée par la series, et moy ne pouvant pas ignorer cette series, j'ay crû mieux faire en la donnant par les logarithmes. Je croyois m'estre expliqué d'une maniere dans la derniere lettre à n'avoir plus laissé d'obscurité. Et pour ce qui est de la correction reïterée, ce n'est que la retractation de la correction, c'est à dire la restitution du premier estat. Car en refaisant le calcul pour vous satisfaire, un abus dans les signes me fit croire que j'avois fait un echange des temps pour les espaces dans les prop. 4 et 6 de l'Article 5. mais depuis j'ay vû qu'il n'y avoit rien à changer comme je vous ay déja mandé. Et lors que vous dites, que s'il est vray que j'aye consideré les resistances de l'air comme en proportion doublée des velocités il faudroit au moins changer l'inscription de l'article 5me, en mettant in proportione quadrata velocitatis, je réponds que si vous aviés consideré ce que je vous avois écritGa naar voetnoot8), vous auriés vû qu'il n'y a rien à changer et je n'aurois pas besoin de repetition mais j'avouë de n'avoir point de droit de vous demander de l'attention. Je dis encor une fois
| |
[pagina 12]
| |
motum a medio retardari proportione velocitatis c'est à dire comme je m'estois expliqué dans le precedent article 4. (dont l'hypothese premiere est la même avec celle du present article 5) que les resistences sont en raison composée des elemens de l'espace ou milieu, et des velocités, et prenant les elemens du milieu pour égaux, ou considerant tout comme égal à l'égard du milieu les resistences sont comme les velocités, car si vous divisés le milieu en parties égales tres petites et le considerés comme egalement parsemé de globules egaux, un grand globe allant la dedans perdra à chaque choc, (c'est à dire à chaque particule du milieu) un degré de vitesse proportionel à la velocité qui luy reste. Et cette consideration a priori m'avoit mené à mon hypothese. Ainsi considerant le milieu comme la base de la division egale (ce qui est le plus naturel) les resistences sont comme les velocités; mais considerant le temps comme la base, c'est à dire divisant le temps en parties egales, tres petites, les resistences ou velocités perduesGa naar einda) à chaque particule de temps, seront comme les quarrés des vistesses. Et la raison est, que les resistances estant en raison composée des elemens de l'espace et des velocités; et les elemens de l'espace estant encor en raison composée des elemens des temps et des velocités, les resistences sont en raison composée des elemens des temps et des quarrés de velocité, ce que je dis en termes expres sous la prop. 3. et comme j'avois deja marqué toutes ces choses, je m'étonne de vôtre conditionelle; s'il est vray que j'aye consideré la proportion doublée; car dans mes precedentes, j'avois expliqué à fonds comment elle avoit lieu, et j'avois rendu raison de mon expression. A parler exactement on ne doit pas direGa naar eindb) que les resistences sont en raison de velocité ny en raison des quarrés des velocités, si ce n'est qu'on adjoute le temps ou le milieu, comme j'ay fait. Enfin on peut examiner à toute rigueur cet article 5, on n'y trouvera rien à dire; il y a seulement une faute à corriger. C'est que l'enontiation de la prop. 3. est toute gâtéeGa naar voetnoot9), je ne scay par quelle megarde; mais cette beveue n'a point d'influence sur tout le reste: Il falloit dire: ResistentiaGa naar eindc) est ad impressionem gravitatis ut quadratum velocitatis acquisita ad quadratum velocitatis maximae; ou bien je pouvois dire quelque chose de semblable à cecy: impressio nova (seu accessio velocitatis), resistentia (seu diminutio velocitatis) et incrementum velocitatis (quod est differentia impressionis et resistentiae) sunt inter se ut quadratum velocitatis maximae, quadratum velocitatis acquisitae, et excessus quadrati maximae super quadratum acquisitae; la preuve de la proposition 3. infere cecy et les preuves des propositions 4. et 6. le supposent, et je ne sçay pas d'ou est venu ce qui pro quo. Mais je laisse enfin ce point sur lequel la seule conside- | |
[pagina 13]
| |
ration que j'ay pour vous m'a rendu si prolixe, à fin de tâcher de vous satisfaire s'il est possible; mais aussi je ne crois pas d'en pouvoir ou devoir dire d'avantage. Vous avés raison, Monsieur, de dire que les courbes que j'avois données pour vôtre probleme sont invariables, et je n'avois pas pris garde que rr/a fait une seule quantité determinée. Mon calcul m'avoit pû mener aussi bien à 2aaxx=aayy-y4 qu'à 2aaxx=aayy+y4, mais ayant la solution qui s'estoit offerte, je n'y avois plus pensé. Vous dites que la premiere se peut quadrer et vous doutés si la seconde se pourroit quadrer aussi, je reponds qu'effectivement il est aussi aisé de quadrer la premiere que de donner un plan egal à la surface decrite par un àrc de cercle tourné à l'entour du diametre; mais la seconde depend de la quadrature de l'Hyperbole. Je ne vous ay pas donné la solution de vos problemes, comme une marque de la perfection de ma Methode, mais comme une marque de son utilité. Je crois meme de vous avoir deja ditGa naar voetnoot10) que pour les resoudre, je ne me suis pas servi de la Methode qui peut toujours reussir pour toutes les lignes ordinaires, car elle est fort prolixe, mais d'une autre, qui est bien plus courte, et bien plus directe et commune aux transcendentes et ordinaires, mais je ne l'ay pas encor mise en perfection pour la pouvoir tousjours conduire jusqu'au bout, parce qu'il y a encor des choses à decouvrir pour applanir des difficultés qui se trouvent dans son chemin. Je n'ay garde de souhaiter qu'on me propose des problemes, dont la solution ne serve qu'à faire croire que je les puisse resoudre. Notre temps est trop pretieux, je suis trop distrait ailleurs pour le present, et la methode pour les lignes ordinaires que je crois suffisante est trop prolixe; il faudroit dresser une espece de tables pour l'abreger, mais je n'en ay pas le loisir. Pour ce qui est des expressions exponentiales, je les tiens pour les plus parfaites de toutes les manieres d'exprimer les transcendentes. Car les Exponentiales donnent une equation finie, ou il n'entre que des grandeurs ordinaires quoy que mises dans l'exposant. au lieu que les series donnent des equations infinies; et les equations differentiales, quoy que finies, employent des grandeurs extraordinaires, sçavoir les differences infiniment petites. Et tout ce que je souhaite pour la perfection de la Geometrie c'est de pouvoir reduire les autres expressions transcendantes aux Exponentiales. Ie ne divise donc pas les courbes Transcendentes en Exponentiales et non exponentiales (comme il semble que vous l'avés pris) mais leurs expressions. Car une meme courbe peut recevoir les trois expressions, que je viens de dire. Par exemple la courbe susdite [qui exprime la relation entre les temps et les vistesses ou bien entre vistesses imprimées par la pesanteur, (qui sont proportionnelles au temps) et entre les | |
[pagina 14]
| |
vistesses absolues, qui en restent à cause de la resistence du milieu] c'est à dire la courbe dont les abscisses sont v et les ordonnées t se peut exprimer serialement par 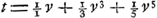 etc. et differentialement par etc. et differentialement par 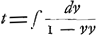 , et enfin exponentialement par , et enfin exponentialement par 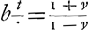 ; ce qui veut dire que ; ce qui veut dire que 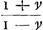 estant comme les nombres, t sont comme les logarithmes; b estant une grandeur constante, dont le logarithme est 1, et le logarithme de 1 estant 0.
Vous faites une demande, Monsieur, à laquelle il est juste que je satisfasse, scavoir si les expressions exponentiales servent à donner quelque description de la courbe et à la marquer en quelque façon par points, ou si je m'en sers seulement à decider que la courbe est transcendente. Je reponds que les expressions exponentiales servent à trouver autant de points qu'on voudra d'une telle courbe, tout comme dans les helices et dans la quadratrice, au lieu que les autres expressions exponentiales servent à trouver autant de points qu'on voudra d'une telle courbe, tout comme dans les helices et dans la quadratrice, au lieu que les autres expressions ordinairement ne donnent pas des points veritables, mais seulement des points approchans; outre qu'elles ne sont pas si maniables par le calcul. Mais il estant comme les nombres, t sont comme les logarithmes; b estant une grandeur constante, dont le logarithme est 1, et le logarithme de 1 estant 0.
Vous faites une demande, Monsieur, à laquelle il est juste que je satisfasse, scavoir si les expressions exponentiales servent à donner quelque description de la courbe et à la marquer en quelque façon par points, ou si je m'en sers seulement à decider que la courbe est transcendente. Je reponds que les expressions exponentiales servent à trouver autant de points qu'on voudra d'une telle courbe, tout comme dans les helices et dans la quadratrice, au lieu que les autres expressions exponentiales servent à trouver autant de points qu'on voudra d'une telle courbe, tout comme dans les helices et dans la quadratrice, au lieu que les autres expressions ordinairement ne donnent pas des points veritables, mais seulement des points approchans; outre qu'elles ne sont pas si maniables par le calcul. Mais il
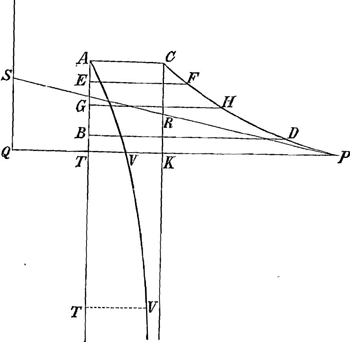 sera bon d'expliquer dans un exemple la maniere de construire ou de marquer des points de la courbe susdite. Soit AC=AB=1 representant la plus grande velocité, et BD droite prise à discretion, soit b. Supposons AC, BD paralleles et cherchant entre elles des moyennes proportionnelles EF, GH, etc. decrivons la courbe des Logarithmes CFHDP. Je dis donc que prenant un point quelconque de cette courbe comme P, et en menant à l'axe AB, une ordonnée PT, alors le | |
[pagina 15]
| |
logarithme ou l'abscisse AT sera t; et le nombre ou l'ordonnée TP sera 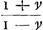 que nous appellerons e. Or e estant assignée il ne reste que de trouver v, ce qui est aisé, car il y aura que nous appellerons e. Or e estant assignée il ne reste que de trouver v, ce qui est aisé, car il y aura 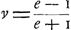 d), c'est à dire dans la droite TP prolongée prenant TK, TQ egales à AC, et erigeant QS normale à QP, et egale à AC, et joignant PS, qui coupera CK (parallele à AB) en R, et enfin dans TP prenant TV égale à KR, il est manifeste que TV sera v, AT estant t; c'est à dire AT estant comme les temps, TV seront comme les velocités, et la ligne AVV asymptote à CK sera la courbe demandée. Il n'est gueres plus difficile de construire les courbes exponentialement exprimées, qui satifont à une de vos soûtangentes, et je m'imagine qu'a present vous serés plus content de ces sortes d'expressions. d), c'est à dire dans la droite TP prolongée prenant TK, TQ egales à AC, et erigeant QS normale à QP, et egale à AC, et joignant PS, qui coupera CK (parallele à AB) en R, et enfin dans TP prenant TV égale à KR, il est manifeste que TV sera v, AT estant t; c'est à dire AT estant comme les temps, TV seront comme les velocités, et la ligne AVV asymptote à CK sera la courbe demandée. Il n'est gueres plus difficile de construire les courbes exponentialement exprimées, qui satifont à une de vos soûtangentes, et je m'imagine qu'a present vous serés plus content de ces sortes d'expressions.
Je seray bien aise de sçavoir si la regle renversée des Tangentes de Mons. Facio contenuë dans les lettres que vous dites avoir receues de luy vous donne quelque contentement, et en quelle sorte de cas vous la trouvés la plus practicable a fin que je puisse juger si elle a quelque rapport à mes meditations. Feu Mons. Gericke m'envoya ses experiences sur un globe de matiere electrique, lorsque son livre n'estoit pas encor imprimé, car je luy avois procuré un privilege de l'Empereur pour ce livre par mes amis. Mais je m'imagine que la substance de ces experiences sera dans le livre, et comme la lettre a esté écriteGa naar voetnoot11) il y a bien du temps, il ne me seroit pas aisé maintenant de la trouver parmy mes vieux papiers. Je seray ravi d'apprendre un jour quelque chose de vos experiences electriques. Pour ce qui est de l'aimant, il est vray que nous ne sçavons pas la regle des declinaisons, je crois neantmoins qu'elles sont reglées avec leurs changemens, et ne dependent pas des causes accidentaires et non liées comme seroient les fibres du globe de la terre suivant ce que GilbertGa naar voetnoot12) et Des CartesGa naar voetnoot13) ont crû. Si elles sont reglées et tant que nous ne sçavons pas comment et pourquoy, c'est une marque que nous n'avons pas encor la vraye hypothese. Je seray bien aise de voir un jour ce qu'on a imprimé en France de la part de l'Academie Royale, sur tout ce qu'il y a de vous. Je me souviens d'avoir aussi remarqué autres fois des voyes de demonstrer la regle de l'equilibre differentes de celle d'Archimede. Mons. Römer me parla aussi d'une sienne, et un Profes- | |
[pagina 16]
| |
seur de Jena nommé WeigeliusGa naar voetnoot14) en a aussi donné. Mais j'ay sur tout envie de voir un jour vôtre maniere, sçachant que vous avés coustume de donner quelque chose d'elegant. J'ay honte de vous parler encore d'une lettre que je vous destine il y a long tempsGa naar voetnoot15) touchant le systeme des Planetes, et qui est demeurée imparfaite par des interruptions, sans que j'aye encor pû la finir. Cependant je m'y mettray au plus tost, et il faut bien aussi que je mette en ordre mes pensées sur la courbe de la chaîne pour les confronter avec les vostres. Les occupations journalieres entierement éloignées de ces choses font que j'ay bien de la peine à reprendre le fil d'un travail interrompu, quand les Idées ne me sont plus recentes. Je souhaitte beaucoup l'honneur de vous voir; mais quand S.A.S. Monseigneur le Duc d'Hanover iroit encor à la Haye, il n'y a pas d'apparence que je le pourrois accompagner, mon employ n'estant pas de suivre la Cour, mais de travailler à des choses dont je suis chargé. Si Dieu me donne la grace de depecher le travail, qui m'occupe à present et qui est de longue haleine, je seray plus libre. Je prie Dieu de vous conserver, dont j'espere de profiter avec le public et je suis avec passion etc.
Monsieur
Vostre tres humble et tres obeissant serviteur Leibniz.
P.S. Quant à la ligne de la chaîne pendante, donnant une oeillade à mon calcul, je m'apperçois que pour la relation entre deux points de la chaîne située dans le meme horison, et entre la partie de la chaîne, pendante dessous, je me puis servir d'une ligne dont l'equation est de la forme de celle que vous aviés marquée xxyy2=a4-aayy2Ga naar voetnoot16). Mais une autre dont je vous avois parlé et dont la forme est xxyy=a4+aayy ne laisse pas d'avoir aussi son usage dans ce probleme.
A Monsieur Monsieur Chr. Hugens Seigneur de Zuylichem. a la Haye. franco Bremen.  |
|