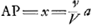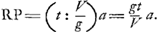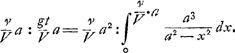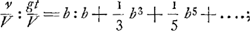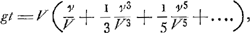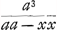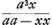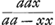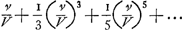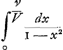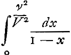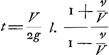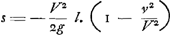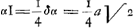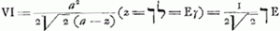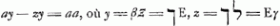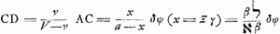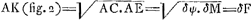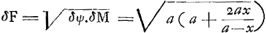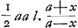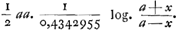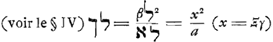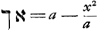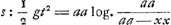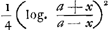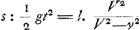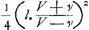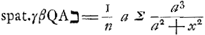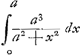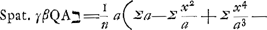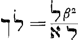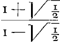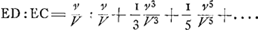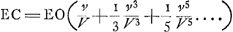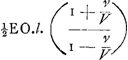Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 23]
| |||||||||||||||||||||
No 2661.
| |||||||||||||||||||||
§ IGa naar voetnoot3).1. Sit ANGa naar voetnoot4) quadratum, cujus latus Aב, diagonalis AN. Referat Aב celeritatem terminalem, sive maximam, quam numquam possit assequi corpus quoddam decidens per aërem, sed quamtumvis prope adaequare. Temporis partes capiantur in recta בN. Quod si igitur descenderet corpus nullo aëre resistente, accrescerent ei celeritatis partes aequales, aequalibus temporis partibus, ut invenit Galileus. Itaque celeritates ita cadentis referant applicatae in triangulo ANΛ parallelae NΛ: sitque celeritas ΛN acquisita tempore בN, corpori nempe non impedito; quam eandem celeritatem maximam seu terminalem esse dixi corporis impediti. Considerentur jam incrementa celeritatis corporis hujus, cui aër resistit; quae cum | |||||||||||||||||||||
[pagina 24]
| |||||||||||||||||||||
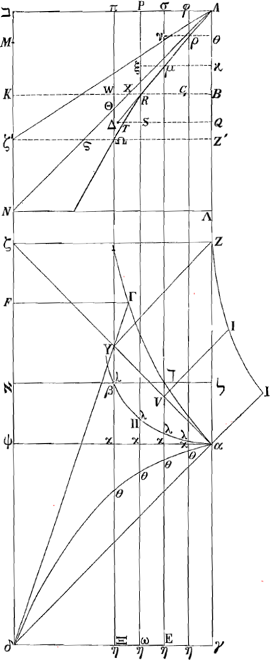 Fig. 1
minora sint incrementis corporis non impediti, sumtis utrobique particulis temporis iisdem, hinc consequitur, ut, si ponatur curva ARΩ, inter quam et rectam | |||||||||||||||||||||
[pagina 25]
| |||||||||||||||||||||
AΛ applicatae, ut RB, referant celeritates acquisitas corpori impeditoGa naar voetnoot5), necessario semper haec minor sit applicata respondente in triangulo ANΛ, ut hic BX. Erunt autem trilinea ARB, ATQ inter se uti altitudines cadendo emensae temporibus AB, AQ; et celeritates in fine aequalium temporum acquisitae, tum motu impedito tum libero, ut applicatae coincidentes ad curvam AR et rectam AN. Velut BR, BX in fine temporis AB. Itemque tempora, quibus eadem celeritas ut ΩZ′ tum impedito tum libero motu acquiretur, ut lineae PΩ et PΘGa naar voetnoot6). Ad examinandam vero naturam curvae ARΩ, sit a puncto ejus aliquo R ducta RS parallela AΛ, eaque temporis particulam referat; sitque S Δ parallela Aב et aequalis ipsi RS: unde juncta R Δ erit parallela AN; secetque S Δ curvam in T puncto. Referet ergo S Δ incrementum celeritatis in tempore RS corporis non impediti; ST vero incrementum celeritatis corporis impediti; ideoque ST minor quam S Δ. Porro si Aב ponatur referre resistentiam, quam pateretur corpus impeditum, si cum terminali celeritate descenderet, velimusque invenire resistentiam, quam patitur acquisita celeritate RB, oportet duabus KB, RB facere tertiam proportionalem CB, quo facto, dico CB referre resistentiam in celeritate RB, quia sunt resistentiae in duplicata ratione celeritatum. Erit autem jam, ut KB ad BC ita S Δ ad Δ T. Quia enim Aב refert resistentiam contra velocitatem terminalem, quae resistentia aequalis est vi gravitatis, qua corpus deorsum pellitur, necesse est in minimis temporum particulis, qualis putanda RS, velocitatem vi gravitatis acquisitam corpori non impedito, quae est S Δ, diminui tali particula T Δ, quae sit ad Δ S ut resistentia tota KB, seu ut vis gravitatis, ad resistentiam CB; atque ita superesse ST velocitatem acquisitam tempore eodem RS corpori impedito: quamobrem tempore WΩ acquiret celeritatem WR, quia ut RS ad ST ita censenda est ΩW ad WR. Sit Aב=a, AP=x. Ergo et RB=x. Et quia proportionales KB, RB, CB, erit KB ad BC, ut a ad xx/a, et BK ad KC ut a ad a - xx/a. Ergo etiam Δ S ad ST, hoc est RS ad ST, hoc est ΩW ad WR, vel etiam Rξ ad ξμ (nam pro recta linea habetur TRμ, cum sit curvae particula minima) ut a ad a-xx/a. Quod si vero | |||||||||||||||||||||
[pagina 26]
| |||||||||||||||||||||
AP in particulas minimas aequales secetur punctis φ, σ, a quibus ducuntur ad curvam AΩ rectae φρ, σμ, parallelae AB, et rursus ρν, μξ complentes rectangula σρ, Pμ: et successive σA, φA, vocentur x, ut ante PA, semper exprimentur rationes μν ad νρ, et ρφ ad φA, rationibus a ad a - xx/a; et erunt invertendo μξ ad ξR, νρ ad μν, Aφ ad φρ, ut a-xx/a ad a. Sunt autem omnes antecedentes μξ, νρ, Aφ, aequales. Ergo si particulis rectae Aπ sumantur particulae ηη aequales in recta γδ, quam aequalem pono Aב, et in quadrato γδψα ducantur parallelae vηϰ; sicut autem ξμ ad ξR, hoc est ut a-xx/a, ita fiat ωϰ=a, ipsi Rξ respondens, ad ωλ; erit
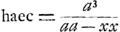 ; et ita exprimentur quoque singulae ηλ, quae erunt ad ϰλ sicut sibi respondentes μν, ρφGa naar voetnoot7), postquam singulae ηγ dicta fuerint x. Jamque sicut omnes simul Aφ, φσ, σP, sive tota AP, ad omnes φρ, νμ, ξR, sive ad totam PR, ita erunt omnes ϰη ad omnes λϰ, atque ita propterea rectangulum αω ad spatium γαΠωGa naar voetnoot8) Et singula spatia ληγα referent singulas rectas spatii RPA singulis λη respondentes.
Haec vero singula spatia, inter λη, αγ, interjecta, mensurantur summa progressionis numericae; singulae enim ; et ita exprimentur quoque singulae ηλ, quae erunt ad ϰλ sicut sibi respondentes μν, ρφGa naar voetnoot7), postquam singulae ηγ dicta fuerint x. Jamque sicut omnes simul Aφ, φσ, σP, sive tota AP, ad omnes φρ, νμ, ξR, sive ad totam PR, ita erunt omnes ϰη ad omnes λϰ, atque ita propterea rectangulum αω ad spatium γαΠωGa naar voetnoot8) Et singula spatia ληγα referent singulas rectas spatii RPA singulis λη respondentes.
Haec vero singula spatia, inter λη, αγ, interjecta, mensurantur summa progressionis numericae; singulae enim 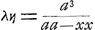 , posito nempe x pro singulis ηγ, quae ipsarum λη distantias ab αγ definiunt; , posito nempe x pro singulis ηγ, quae ipsarum λη distantias ab αγ definiunt; 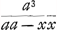 vero aequale vero aequale 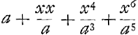 etc., et si pro a unitas ponatur, fit 1+xx+x4+x6+etc.; ac porro, si maxima linearum ηγ, ut hic ωγ, vocetur b; et x successive significet aequaliter crescentes γη, quarum minima, sive excessus, quibus crescunt, dicatur p; et numerus particularum p in ωγ seu b comprehensarum dicatur θ; erit quae ab αγ etc., et si pro a unitas ponatur, fit 1+xx+x4+x6+etc.; ac porro, si maxima linearum ηγ, ut hic ωγ, vocetur b; et x successive significet aequaliter crescentes γη, quarum minima, sive excessus, quibus crescunt, dicatur p; et numerus particularum p in ωγ seu b comprehensarum dicatur θ; erit quae ab αγ
| |||||||||||||||||||||
[pagina 27]
| |||||||||||||||||||||
Est autem γω fractio unitate minor, quia γδ est unitas, unde fit ut membra progressionis ejusmodi continue decrescant, atque eo magis quo γω minor pars fuerit γδGa naar voetnoot9). | |||||||||||||||||||||
§ IIGa naar voetnoot10).Hanc vero progressionem aequari sectori hyperbolico NewtoniGa naar voetnoot11) inde inveni, quod eadem progressione sector ille efficitur; quod et aliter animadvertere potui | |||||||||||||||||||||
[pagina 28]
| |||||||||||||||||||||
ex quadraturis Mercatoris et WallisiiGa naar voetnoot12), quam hic illum imitatus procudit. Posita enim hyperbola BG, cujus asymptoti AH, AE, quadratum vero AB; sumtâque
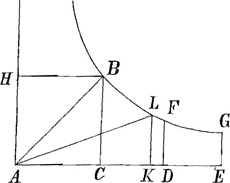 Fig. 2
AD majore quam AC; si AD sit=i; DE vero fractio minor unitate, quae fractio vocetur bGa naar voetnoot13), fit ex quadratura Nicolai Mercatoris spatium FDEG ad quad. HC ut b-½b2+⅓b3-¼b4+⅕b5- etc. ad 1.
Item posita DC=DE, fit ex quadratura Wallisii spatium FBCD ad quad. HC ut
Ergo spatium BGEC ex duobus illis compositum erit ad quadr. BA ut | |||||||||||||||||||||
[pagina 29]
| |||||||||||||||||||||
2b+⅔b3+⅖b5+ etc. ad 1; quam progressionem singulos terminos duplos habere apparet nostrae praecedentis progressionis b+⅓b3+⅕b5+ etc. Unde et nostram aequari constatGa naar voetnoot14) spatio ejusmodi hyperbolico, quod nempe dimidium erit spatii BGEC, hoc est spatio BLKC, sive sectori hyperbolico Newtoni BAL, positâ AK media proportionali inter AC, AE; sic enim fiunt quoque proportionales BC, LK, GE, ideoque spatia BLKC, LGEK inter se aequalia. Hinc optima ratio progressionum ad inveniendos logarithmos, praecipue si CD sit ad DA ut unitas ad numerum, hoc est, si EA ad AC sit ut numerus ad alium binario vel unitate minorem. Sed de his alias. vid. pag. 46 et 45Ga naar voetnoot15). | |||||||||||||||||||||
§ IIIGa naar voetnoot16).Spatio nostroGa naar voetnoot17), quod nunc sit αβΞγ, aequalis debebat esse sector hyperbolicus Newtoni αΓδGa naar voetnoot18) ducta δΓ per Y, ubi rectam αζ perpend. in αδ secat Ξβ producta; est autem αΓ hyperb. ad asymptotos δγ, δΝ. Sicut enim Απ ad πΩ ita est rectangulum αΞ ad spatium αβΞδGa naar voetnoot19), ex demonstrata curvarum harum naturaGa naar voetnoot20). Quare et πΘ erit ad πΩ ut rectangulum αΞ ad spatium αβΞδGa naar voetnoot19). Est autem πΘ ad πΩ ut | |||||||||||||||||||||
[pagina 30]
| |||||||||||||||||||||
tempus, quo corpus non impeditum acquisivit celeritatem ΩZ′, ad tempus quo corpus impeditum acquisivit celeritatem eandem. Jam quia Newtonus, posita celeritate acquisita ad celeritatem terminalem ut αY ad αζ, quarum ratio est eadem quae Aπ ad Aב, quam nos adsumsimus, invenit tempus descensus non impediti ad tempus impediti, quibus obtinetur celeritas eadem αY, sicut triangulum αδY ad sectorem hyperbolicum αδΓ: estque triang. αδY aequale rectangulo nostro αΞGa naar voetnoot21); necesse est et sectorem αδΓ aequari spatio nostro αβΞγ, si recte se habent inventa Newtoni; unde primum didici progressionem meam b+⅓b3+⅕b5+ etc. aequari spatio hyperbolico. | |||||||||||||||||||||
§ IVGa naar voetnoot22).Ut inquiramus porro quam rationem habeat altitudo emensa motu impedito, dum acquiritur celeritas data Z′Ω, ad altitudinem eodem tempore πΩ emensam cum celeritate dimidia celeritatis terminalis, scimus primum haec spatia esse inter se sicut trilineum AΩZ′ ad dimidium rectanguli בZ′, sive ad triangulum AζZ′Ga naar voetnoot23). Jam cum sit spat. AΩπ ad rectang. πZ′ ut omnes φρ, σμ, PR, πΩ ad totidem maximae πΩ aequales; hoc est, sicut summa spatiorum omnium αληγ ad totidem maximo βαγΞ aequaliaGa naar voetnoot24); hoc est, ut cuneus anguli semirecti super spatio αβΞγ per βΞ abscissus, ad prisma super eodem spatio αβΞγ cum altitudine γΞ: sequitur hinc trilineum alterum AΩZ′ esse ad dictum rectang. πZ′, ut cuneus alterGa naar voetnoot25) super spatio αβΞγ abscissus per αγ ad idem prisma super spatio αβΞγ; quia constat hunc cuneum | |||||||||||||||||||||
[pagina 31]
| |||||||||||||||||||||
cum priori constituere simul prisma jam dictum, sicut trilinea AΩπ et AΩZ′ constituunt rectangulum πZ′. Atqui cuneus super spatio αβΞγ abscissus per αγ aequalis est ei, quo cuneus super rectangulo βγ, abscissus per לγ, superat cuneum simul abscissum super spatio trilineo αβל: quem cuneum ajo aequalem esse prismati super trilineo hyperbolico αךל, altitudinem habenti dimidiam δγ. Quod hoc modo demonstro. Si enim ducatur recta aliqua, ut אל, parallela γδ, ac secans curvam αλλ, ut hic in β, fiatque duabus אל, βל tertia proportionalis ךל, erit punctum ך ad hyperbolam αךΓ ante descriptamGa naar voetnoot25) per α punctum ad asymptotos δב, δγ. Nam ponendo אל=a, βל=x, inventum fuit supraGa naar voetnoot26) esse βΞ, quae vocetur y, aequalem 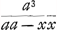 ; unde erit βל sive ; unde erit βל sive 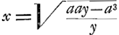 ; et, quia אל est a, invenitur tertia proport. duabus אל,
βל quae erat ךל, aequalis ay-aa/y; sit ךל=z, ergo ay-aa=zy, et ay-zy=aa. Unde liquet punctum ך esse ad hyperbolam dictam, quae per α punctum ad asymptotos δב, δγ descripta est. Quia itaque אל, quae secat curvam αλ in β et hyperbolam αךΓ in ך, ita iis punctis dividitur, ut sint proportionales אל, βל, ךל, erit rectang. ex אל, לך aequale quadrate ex βל: quod cum semper eveniat, ubicumque ducatur recta ipsi אל parallela, sequitur, si tales parallelae ducantur in rectangulo אα, quae latus ejus אψ in particulas aequales dividant, fore omnia rectangula ex ductu harum parallelarum in partes earum inter αל et hyperbolam αך interceptas, aequalia omnibus quadratis partium interceptarum inter αל et curvam αλβ. Vel, sumtis omnium dimidiis, erit summa rectangulorum ex omnibus interceptis spatii ךל in dimidias לא, aequalis summae semiquadratorum ab omnibus interceptis in spatio αβל, atqui ista summa rectang. efficit prisma super spatio αךל, cum altitudine ½ אל. Similique ratione summa illa semiquadratorum essicit cuneum super spatio αβל abscissum
per αל angulo semirecto. Ergo illud prisma huic cuneo aequale est, ut dicebamus. ; et, quia אל est a, invenitur tertia proport. duabus אל,
βל quae erat ךל, aequalis ay-aa/y; sit ךל=z, ergo ay-aa=zy, et ay-zy=aa. Unde liquet punctum ך esse ad hyperbolam dictam, quae per α punctum ad asymptotos δב, δγ descripta est. Quia itaque אל, quae secat curvam αλ in β et hyperbolam αךΓ in ך, ita iis punctis dividitur, ut sint proportionales אל, βל, ךל, erit rectang. ex אל, לך aequale quadrate ex βל: quod cum semper eveniat, ubicumque ducatur recta ipsi אל parallela, sequitur, si tales parallelae ducantur in rectangulo אα, quae latus ejus אψ in particulas aequales dividant, fore omnia rectangula ex ductu harum parallelarum in partes earum inter αל et hyperbolam αך interceptas, aequalia omnibus quadratis partium interceptarum inter αל et curvam αλβ. Vel, sumtis omnium dimidiis, erit summa rectangulorum ex omnibus interceptis spatii ךל in dimidias לא, aequalis summae semiquadratorum ab omnibus interceptis in spatio αβל, atqui ista summa rectang. efficit prisma super spatio αךל, cum altitudine ½ אל. Similique ratione summa illa semiquadratorum essicit cuneum super spatio αβל abscissum
per αל angulo semirecto. Ergo illud prisma huic cuneo aequale est, ut dicebamus.
| |||||||||||||||||||||
[pagina 32]
| |||||||||||||||||||||
Est autem et cuneo super rectang. βγ, abscisso per αγ, aequale prisma super rectangulo ךγ cum altitudine ½ אל, propter proportionales אל, βל, ךל. Ergo, cum ante ostensum fuerit id, quo cuneus super rectang. βγ, per αγ abscissus, superat cuneum simul abscissum super spatio αβל, aequari cuneo super spatio αβΞγ per αγ abscisso; erit hic cuneus aequalis differentiae, qua prisma dictum super rectang. ךγ cum altitudine ½ אל superat prisma super spatio αךל cum eadem altitudine ½ אל; hoc est prismati super spatio αךEγ cum dicta altitudine ½ אל. Ostensum vero fuit trilineum AΩZ′ esse ad rectang. πZ′ ut cuneus super spatio αβΞγ per αγ abscissus ad prisma super spatio αβΞγ cum altitudine γΞ. Ergo jam erit trilineum AΩZ′ ad rectang. πZ′ ut prisma super spatio αךEγ cum altitudine ½ אל ad prisma super spatio αβΞγ cum altitudine γΞ, hoc est in ratione composita ex ratione spatii αךEγ ad spatium αβΞγ, et ex ratione ½ אל ad βל. Est autem rectang. πZ′ ad triangulum Aζ᾽Z′ ut ΩZ′ ad dimidiam ζ᾽Z′, sive ut βל ad ½ אל. Ergo, cum ratio triang. Aζ᾽Z′ ad spatium AΩZ′ componatur ex ratione triang. Aζ᾽Z′ ad rec. πZ′, et rectanguli πZ′ ad spatium AΩZ′; erit jam ratio trianguli Aζ᾽Z′ ad spatium AΩZ′ composita ex ratione ½ אל ad βל et spatii αβΞγ ad spatium αךEγ, et βל ad ½ אל, quae posterior ratio tollit primam. Ergo erit triang. Aζ᾽Z′ ad spatium AΩZ′ ut spatium αβΞγ ad spatium αךEγGa naar voetnoot27). Ergo hanc eandem rationem habebit quoque altitudo emensa tempore AZ′ cum celeritate dimidia terminali ad altitudinem eodem tempore AZ′ emensam casu impedito. Quod erat inveniendumGa naar voetnoot28). | |||||||||||||||||||||
[pagina 33]
| |||||||||||||||||||||
§ VGa naar voetnoot29).Et convenit cum Newtonianis prop. 9 Lib. 2Ga naar voetnoot30). Sed corrigendum ibi in. 7 et 10 ac legendum ABNK pro ABRP. Et lin. [8] pro: cum semisse velocitatis maximae, legendum cum velocitate maxima; sicut recte postea pag. eadem ubi, de ascensuGa naar voetnoot31). Fit enim ipsius spatium hyperbolicum ABNK, quod in meo sche- | |||||||||||||||||||||
[pagina 34]
| |||||||||||||||||||||
mateGa naar voetnoot32) est αIIV, dimidium mei αךEγGa naar voetnoot33). Invenitur autem spatio αβΞγ aequale spatium hyperbolicum, quod sit loco sectoris αΓδ, si ponatur ut אβ ad βל ita δψ ad ψζGa naar voetnoot34) et sumatur ipsi ψζ aequalis ψMGa naar voetnoot35); interque Mδ, δψ inveniatur media proportionalis Fδ: et fiat FΓ
parall. בA. Erit enim spatium αψFΓ aequale spatio αβΞγGa naar voetnoot36); quod logarithmis jam exprimi potest. Est enim = 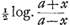 Ga naar voetnoot37). Ponendum autem quadr. αδ sive aa=0,4342955, qualium log. 10 est 1,0000000. Quod si x sit=½ a, fit jam spatium αβΞγ=½ log. 3. Similiter spa- Ga naar voetnoot37). Ponendum autem quadr. αδ sive aa=0,4342955, qualium log. 10 est 1,0000000. Quod si x sit=½ a, fit jam spatium αβΞγ=½ log. 3. Similiter spa- | |||||||||||||||||||||
[pagina 35]
| |||||||||||||||||||||
tium αךEγ, logarithmo expressum, fit= 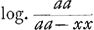 ; et, si x=½a, log. 4/3. Est enim spatium αךEγ, relatum ad quadr. αδ, aequale logarithmo rationis VEGa naar voetnoot38) ad αγ, sive αψ ad דא, hoc est a ad a-xx/aGa naar voetnoot39), sive aa ad aa-xx. ; et, si x=½a, log. 4/3. Est enim spatium αךEγ, relatum ad quadr. αδ, aequale logarithmo rationis VEGa naar voetnoot38) ad αγ, sive αψ ad דא, hoc est a ad a-xx/aGa naar voetnoot39), sive aa ad aa-xx.
| |||||||||||||||||||||
§ VIGa naar voetnoot40).Invenio autem et rationem trilinei AΩZ′ ad triang. AςZ′, hoc est rationem altitudinis emensae casu impedito ad altitudinem emensam eodem tempore casu non impedito, [donec utrimque perveniatur ad celeritatem datam Aπ]Ga naar voetnoot41), esse in ratione composita ex ratione spatii αךEγ ad αβΞγ et quadrati αδ ad αβΞγ, hoc est, ex ratione composita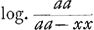 ad ad 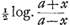 et aa ad et aa ad 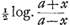 . Et in numeris sit x=½a, erunt istae altitudines in ratione composita ex ratione log. 4/3 ad ½ log. 3 et aa ad ½ log. 3. Et posito aa ∞ 0,4342955 secundum ultimam nostram quadraturam hyperbolaeGa naar voetnoot42), log. 4/3 est 0,1249388, log. 3 . Et in numeris sit x=½a, erunt istae altitudines in ratione composita ex ratione log. 4/3 ad ½ log. 3 et aa ad ½ log. 3. Et posito aa ∞ 0,4342955 secundum ultimam nostram quadraturam hyperbolaeGa naar voetnoot42), log. 4/3 est 0,1249388, log. 3
| |||||||||||||||||||||
[pagina 36]
| |||||||||||||||||||||
est 0,4771212; ut 5,426035861540 ad 5,691115987236, fere ut 20 ad 21Ga naar voetnoot43). Ratio enim spatii AΩZ′ ad triang. AςZ′ componitur ex rationibus spatii AΩZ′ ad rectang. πZ′ et rectanguli πZ′ ad triang. AςZ′. Sed ostensum estGa naar voetnoot44) rationem spatii AΩZ′ ad rect. πZ′ componi ex ratione spatii αךEγ ad spat. αβΞγ, et ex ratione ½ אל ad βל. Rationem vero alteram, rectanguli πZ′ ad triangulum AςZ′, constat eandem esse, quae ΩZ′ ad ½ Z′ς, hoc est, quae πΘ ad ½ πΩ, hoc est, quae rectanguliGa naar voetnoot45) αΞ ad ½ spat. αβΞγ, quae, posito ss pro spatio αβΞγ, est eadem compositae ex αγ seu אל ad s, et γΞ sive βל ad ½ s. Itaque ratio spatii AΩZ′ ad triang. AςZ′ erit composita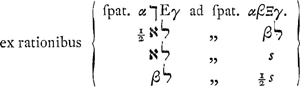 hoc est, quia βל se mutuo tollunt, ex rationibus αךEγ ad spatium αβΞγ, et ½ quadr. אל ad ½ ss, seu ½ αβΞγ; sive et quadrati אל seu αδ ad spat. αβΞγ. Quod erat demonstrandum. | |||||||||||||||||||||
§ VIIGa naar voetnoot46).Est autem πΘ ad πΩ ut tempus quo grave, cadens libere, acquireret celeritatem dimidiam maximae, ad tempus quo eandem celeritatem acquireret motu impedito. Sed si in universum celeritas data sit pars quaevis maximae celeritatis; tunc tempus descensus liberi, ad tempus descensus impediti hic est ut ▭ ax ad spatium αβΞγGa naar voetnoot47). Hoc est ut ax ad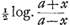 . .
| |||||||||||||||||||||
[pagina 37]
| |||||||||||||||||||||
NB. x hic lineam significat, partem scilicet γδ rectae; item a totam γδ. Itaque ax semper est portio certa quadrati aa.
ut ▭ αΞ ad spatium αβΞγ. hoc est ut πΘ ad πΩ, hoc est ut ½ aa ad ½ log. 3, fere ut 10 ad 11. Qui nostra quadratura hyperbolae non utuntur quae est in Additione dissertationis de causa gravitatis necessario adhibere debent reductionem logarithmorum ordinariorum, diminuend. eos in ratione 10000000 ad 4342955. | |||||||||||||||||||||
§ VIIIGa naar voetnoot49).Colligitur igitur ex jam demonstratis, si velocitates aequaliter crescentes dicantur x, maxima seu terminalis velocitas sit a, tempora fore sicut summas rectarum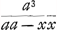 , quod recte habet et Leibnitius. Spatia vero cadendo emensa, ut summae , quod recte habet et Leibnitius. Spatia vero cadendo emensa, ut summae  , cum Leibn. habeat summas , cum Leibn. habeat summas  . Tempora vero, sive summas rectarum . Tempora vero, sive summas rectarum 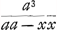 , fore , fore 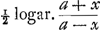 , (hic x significat velocitatem in fine temporis acquisitam, ut in reliquis deinceps, et deberet pro eo scribi X majus) ubi Leibnitius habet , (hic x significat velocitatem in fine temporis acquisitam, ut in reliquis deinceps, et deberet pro eo scribi X majus) ubi Leibnitius habet 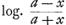 , seu, quia ponit a=1, , seu, quia ponit a=1, 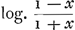 . Recte quidem dixerat tempora esse ut logarithmos rationis a+x ad a-x, sed non bene videtur scribere . Recte quidem dixerat tempora esse ut logarithmos rationis a+x ad a-x, sed non bene videtur scribere 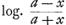 pro logarithmo rationis a+x ad a-x, quia talis fractionis logarithmus sit negativus. Non erravit etiam, quod tempora dixerit esse ut logarithmos rationis a+x ad a-x, cum tamen mihi sint ut ½ logarithmi rationis hujus a+x ad a-x: quia eadem est ratio logarithmorum ac ½ logarithmorum inter se. Sed tunc pro tempore quo, casu non impedito, acquiritur velocitas ter- pro logarithmo rationis a+x ad a-x, quia talis fractionis logarithmus sit negativus. Non erravit etiam, quod tempora dixerit esse ut logarithmos rationis a+x ad a-x, cum tamen mihi sint ut ½ logarithmi rationis hujus a+x ad a-x: quia eadem est ratio logarithmorum ac ½ logarithmorum inter se. Sed tunc pro tempore quo, casu non impedito, acquiritur velocitas ter- | |||||||||||||||||||||
[pagina 38]
| |||||||||||||||||||||
minalis, non est ponendum hyperbolae
quadratum aa sive 1, ut Newtonus fecitGa naar voetnoot50) et ipse voluit, ut puto, Leibnitius. Invenio etiam spatia descendendo emensa fore ut logarithmos 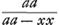 , cum Leibnitius habeat log. , cum Leibnitius habeat log. 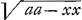 vel log. vel log. 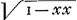 . Rursus hic inverse posuisse videtur pro logarithmo rationis aa ad aa-xx, logarithmum aa-xx/aa, sive quia aa est unitas, logarithmum (1-xx). Sed cum ponat log. . Rursus hic inverse posuisse videtur pro logarithmo rationis aa ad aa-xx, logarithmum aa-xx/aa, sive quia aa est unitas, logarithmum (1-xx). Sed cum ponat log. 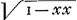 , erravit rursus, quia debebat dicere log. 1-xx, ut posset referri ad aa=1. Nam alioquin eadem est ratio logarithmorum radicum, quae logarithmorum quadratorum ab iisdem radicibus, ut jam antea dictum fuit. Puto ipsum vice versa errasse in apponendo signo √ adeoque, ubi ½ , erravit rursus, quia debebat dicere log. 1-xx, ut posset referri ad aa=1. Nam alioquin eadem est ratio logarithmorum radicum, quae logarithmorum quadratorum ab iisdem radicibus, ut jam antea dictum fuit. Puto ipsum vice versa errasse in apponendo signo √ adeoque, ubi ½ 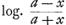 seu log. seu log. 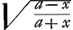 scribere debuerat, scripsisse scribere debuerat, scripsisse 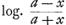 .
Et ubi debebat esse log. (1-xx) scripsisse log. √(1-xx), et tamen saepius jam calculum suum correxerat.
A ב seu בN est ad ΩπGa naar voetnoot51) ut quad. αδ ad spat. αβΞγ, seu ad .
Et ubi debebat esse log. (1-xx) scripsisse log. √(1-xx), et tamen saepius jam calculum suum correxerat.
A ב seu בN est ad ΩπGa naar voetnoot51) ut quad. αδ ad spat. αβΞγ, seu ad 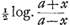 ; si quad. αδ sit quadr. hyperbolae. Et posito hoc quadrato=43429, etc., uti poterimus logarithmis tabul. ; si quad. αδ sit quadr. hyperbolae. Et posito hoc quadrato=43429, etc., uti poterimus logarithmis tabul.
| |||||||||||||||||||||
§ IXGa naar voetnoot52).Notatu dignum quod spatium AΩZ′ semper dimidium est spatii hyperbolici ךαγE. | |||||||||||||||||||||
[pagina 39]
| |||||||||||||||||||||
Nam cum spatium αβΞγ sit ad rectang. αΞ ut Ωπ ad πAGa naar voetnoot53), ex ante demonstratis, hoc est ut rectang. Aζ′ ad rectang. ex A ב, Aπ, seu rectang. αΞ; sequitur hinc spatium αβΞγ aequari rectang. Aζ′. Atqui ostensum fuitGa naar voetnoot54) triangulum Aζ′Z′, seu ½ rectang. Aζ′, esse ad spatium AΩZ′, ut spatium αβΞγ ad spatium αךEγ; ergo etiam ½ spatii αβΞγ ad spat. AΩZ′ ut spatium totum αβΞγ ad spat. αךEγ. Et permutando ut 1 ad 2, ita spat. AΩZ′ ad spat. hyperbolicum αךEγ. | |||||||||||||||||||||
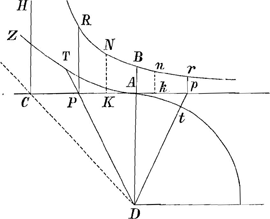
§ XGa naar voetnoot55).2. Sit quadratum בVGa naar voetnoot56), cujus diagonalis AN. Latus vero Aב referat celeritatem terminalem, quam superare non possit grave per aërem cadens. Ponatur autem nunc illa celeritate terminali sursum projici. Et quaeratur primum tempus totius ascensus impediti, seu ratio ejus ad tempus totius ascensus non impediti, atque etiam altitudo totius ascensus impediti ad altitudinem totius ascensus non impediti. Scimus celeritatem sursum libere tendentis diminui aequaliter aequalibus temporis partibus. Ideoque si tempora talis ascensus accipiantur in latere quadrati בN, quo totius ascensus tempus designetur, celeritates recte designari per applicatas in triangulo NבA, lateri Aב parallelas. Veluti, si tempus ascensus sit בB, celeritatem corporis non impediti in fine ejus temporis fore BX, ratione nimirum celeritatis terminalis Aב. Sed celeritatem reliquam in motu impedito, exacto tempore eodem בB, constat minorem fore quam BX. Sit ergo BR; sitque curva ARG, cujus applicatae ad Nב referant celeritates relictas in motu impedito. Totum vero tempus ascensus impediti erit Gב, ac minus quidem tempore ascensus liberi בN. Jamque altitudo tota ascensus impediti ad non impediti erit ut spatium ARGב ad triangulum AבN; quoniam utraque altitudo fit ex particulis temporis in celeritates iis temporum particulis existentes. Ad inquirendum vero naturam curvae ARG, sit e puncto ejus aliquo R ducta recta minima RS parallela בN, et ST parallela Aב, quae occurrat curvae in T; | |||||||||||||||||||||
[pagina 40]
| |||||||||||||||||||||
sitque R Δ parallela AN. Referet ergo S Δ decrementum celeritatis non impeditae per temporis particulam RS, impeditae vero celeritatis decrementum per tempus idem RS erit ST, ut quidem S Δ sit ad Δ T sicut quadratum KB ad quadratum RB; quia resistentiae sunt in duplicata ratione celeritatum. Et in minimo tempore eandem rationem habere recte censentur particulae celeritatis amissae, quam resistentiae ipsas producentes: Erat autem S Δ particula celeritatis amissa
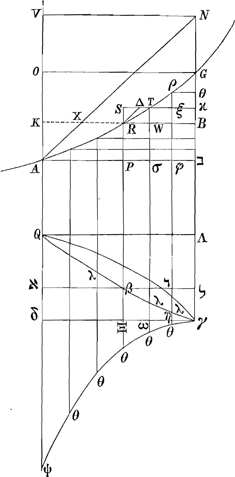 Fig. 3.
ex resistentia gravitatis, sive etiam quam resistentia tota terminalis tempore RS effectura erat. | |||||||||||||||||||||
[pagina 41]
| |||||||||||||||||||||
Quod si igitur A ב sit a, et BR celeritas=x; erit S Δ ad Δ T sicut aa ad xx; et ST ad S Δ ut aa+xx ad aa. Unde et ST ad SR, sive RW ad WT, ut aa+xx ad aa. Si divisa igitur intelligatur tota ב A in particulas aequales Pσ, σφ, φב etc. Itemque PR, σT, φρ ad curvam AG, et rursus RW, Tξ, ρθ, erit in singulis trilineis minimis RWT, Tξρ, ρθG, basis ad perpendicularem, ut aa++xx ad aa, si nempe vocentur successive x applicatae RB, Tϰ, ρθ, quae fiunt productis basibus istis. Sit δψ=δA; et γθψ parabola vertice γ. Ad hanc continuatae RP, Tσ, ρφ, facient singulas Pθ, σθ, φθ=a+xx/a; unde, si fiunt duabus θP, ΞP tertia proport. βP, et sic porro, erunt singulae βP, λσ, λφ=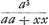 ; hoc est rationes ΞP ad βP, ωσ ad λσ, ηφ ad λφ, etc. singulae eaedem, quae RW ad WT, Tξ ad ξρ, ρθ ad θG; ideoque quadratum totum Aγ ad spatium γβQAב, ut recta בA, seu בN, ad בG. Atqui, ob singulas λφ, λσ, βP= ; hoc est rationes ΞP ad βP, ωσ ad λσ, ηφ ad λφ, etc. singulae eaedem, quae RW ad WT, Tξ ad ξρ, ρθ ad θG; ideoque quadratum totum Aγ ad spatium γβQAב, ut recta בA, seu בN, ad בG. Atqui, ob singulas λφ, λσ, βP=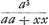 , constat ex Nic. Mercatoris methodo, secundum Leibnitsii quadraturam circuli, summam omnium harum, hoc est spatium γβQAב esse aequale circulo intra quadr. Aγ inscriptoGa naar voetnoot57). , constat ex Nic. Mercatoris methodo, secundum Leibnitsii quadraturam circuli, summam omnium harum, hoc est spatium γβQAב esse aequale circulo intra quadr. Aγ inscriptoGa naar voetnoot57).
Ergo ut quadratum ad circulum sibi inscriptum, ita est hic Nב tempus ascensus liberi ad Gב tempus ascensus impediti. Ad altitudinum porro rationem investigandam, quae sunt hic ut triang. ANב ad spatium AGב, constat, ex jam dictis, rectam ρφ referri spatio AφλQ, rectam Tσ spatio AσλQ, atque ita porro. Unde omnium ρφ, Tσ, etc. summa, hoc est spatium GבΛ refertur summa omnium AφλQ, AσλQ etc., hoc est cuneo anguli semirecti super spatio בAQβγ abscisso per בγ. | |||||||||||||||||||||
[pagina 42]
| |||||||||||||||||||||
Hujus vero cunei solidum ut noscatur, fiat duabus אל, βל tertia proportionalis ךל; erit jam punctum ך ad hyperbolam transeuntem per γQ, habentemque asymptoton בA. Quia enim, posita βל=x, inventa fuit βP= 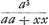 , ךל autem est xx/a; si βP sive בל vocetur y, et ךל vocetur z, erit , ךל autem est xx/a; si βP sive בל vocetur y, et ךל vocetur z, erit 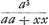 =y, et xx/a = z, five xx=az, unde, restituto valore xx, erit =y, et xx/a = z, five xx=az, unde, restituto valore xx, erit 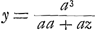 , sive , sive 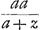 , atque adeo ay+zy=aa, unde facile apparet punctum ך esse ad hyperbolam γךQ, uti diximus. Quia porro rectang. אלך aequale est quadrato ex βל, idque in omnibus applicatis parallelis, erit prisma super spatio γךQΛ, cum altitudine δγ, aequale quadratis omnibus βל et reliquarum applicatarum ad curvam γβQ. Ideoque prismatis illius dimidium aequale cuneo super spatio γβQΛ abscisso per γΛ. Est autem et prismatis super rectangulum AΛ cum altitudine δγ dimidium aequale cuneo super idem
rectangulum AΛ per בΛ abscisso. Ergo prisma super spatio toto γךQAב cum dimidio altitudinis δγ aequabitur cuneo super spatio toto γβQAב abscisso per בγ. , atque adeo ay+zy=aa, unde facile apparet punctum ך esse ad hyperbolam γךQ, uti diximus. Quia porro rectang. אלך aequale est quadrato ex βל, idque in omnibus applicatis parallelis, erit prisma super spatio γךQΛ, cum altitudine δγ, aequale quadratis omnibus βל et reliquarum applicatarum ad curvam γβQ. Ideoque prismatis illius dimidium aequale cuneo super spatio γβQΛ abscisso per γΛ. Est autem et prismatis super rectangulum AΛ cum altitudine δγ dimidium aequale cuneo super idem
rectangulum AΛ per בΛ abscisso. Ergo prisma super spatio toto γךQAב cum dimidio altitudinis δγ aequabitur cuneo super spatio toto γβQAב abscisso per בγ.
Est autem prisma super γβQAב ad cuneum super idem γβQAב per γב, ut rectang. Oב ad trilineum GבA. Ergo etiam prisma super γβQAב cum altitudine δγ, ad prisma super γךQAב cum ½ altitudine δγ, ut rectangulum Oב ad trilineum GבA. Ergo et spatium γβQAב ad ½ spat. γךQAב ut rectangulum Oב ad trilineum GבA. Sed per ante ostensa erat quadratum בδ ad spat. γβQAב ut quadr. Vב ad rectangulum בO, sunt enim haec ut Nב ad Gב. Itaque jam ex aequo erit quadr. בδ ad ½ spatium γךQAב ut quadratum Vב ad trilin. GבA. Sunt autem quadrata בδ, Vב aequalia; ergo et ½ spatium hyperbolicum γךQAב aequale trilineo GבA, unde et ½ spat. γךQAב ad ½ quadr. בδ; seu totum ad totum, ut trilineum GבA ad ½ quadr. בδ sive ½ quadr. בV; quod erat inveniendum. Est autem spatium hyperbolicum γךQAב ad quadr. בδ ut logar. binarii ad quadratum hyperbolaeGa naar voetnoot58), hoc est ut fere 30103 ad 43430. Ergo hanc rationem habebit altitudo ascensus impediti, incipientis cum celeritate terminali, ad altitudinem ascensus liberi, eadem cum celeritate incipientis. | |||||||||||||||||||||
[pagina 43]
| |||||||||||||||||||||
§ XIGa naar voetnoot59).Invenire rationem inter tempus descensus ad tempus ascensus cum corpore projicitur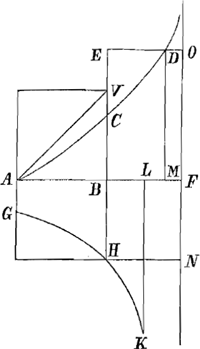 Fig. 4
sursum celeritate terminali. Curva ad ascensum ACGa naar voetnoot60). Curva ad descensum CD. Oportet spatia ABC, CED esse aequaliaGa naar voetnoot61). Quaeritur ratio BC ad CE quae est temporum. AB=BF=BH. GHK hyperbola ad asymt.os AF, FN. Spat. ABC=½ ABHGGa naar voetnoot62). BL=LF. Spatium HBLK=ABHG. Ergo debet esse spat. CDE=½ spat. HBLK. BM media prop. inter BF, BL. MD parall. BE. Dico spatium CDE aequari CBAGa naar voetnoot63). Si enim BF=1, erit BL=½, et BM=√½. [UndeGa naar voetnoot64) ex supra demonstratis, log.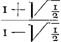 =spat. HBLK. Ex iisdem vero =spat. HBLK. Ex iisdem vero
| |||||||||||||||||||||
[pagina 44]
| |||||||||||||||||||||
est OE ad EC ut quad. BN ad ½ spat. HBLK, hoc est ad ½ log. 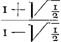 ]. ].
Atqui BC ad BV seu OE ut circulus inscriptus qu. AV seu quo BN ad ipsum | |||||||||||||||||||||
[pagina 45]
| |||||||||||||||||||||
qu.um BNGa naar voetnoot65). Ergo ex aequo BC ad EC ut circulus in quadr. BN ad ½ log. 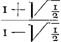 seu ½ log. seu ½ log. 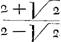 .
14 - 11 - 4343 - 3412 ½ log. .
14 - 11 - 4343 - 3412 ½ log. 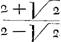 =3826,8 =3826,8
3827:3412 ut tempus descensus ad tempus ascensus prox.e cum projicitur celeritate terminali. |
| ||||||||||||||||||||