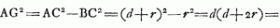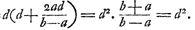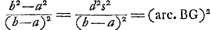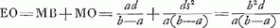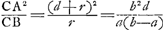|
| |
| |
| |
No 2693.
Christiaan Huygens à G.W. Leibniz.
1er septembre 1691.
La lettre se trouve à Hannover, Bibliothèque royale.
La minute se trouve à Leiden, coll. Huygens.
La lettre a été publiée par P.J. UylenbroekGa naar voetnoot1) et C.I. GerhardtGa naar voetnoot2).
Elle est la réponse aux Nos. 2682 et 2688.
Leibniz y répondit le 21 septembre 1691.
Sommaire:Ga naar voetnoot3)
S'il l'a fait expresGa naar voetnoot4) de ne marquer pas la raison de א à בGa naar voetnoot5), ni que AΘGa naar voetnoot6) est la soustangente de la Logarithmique? J'ay bien reconnu, en conferant vostre construction avec celle de Mr. Jo. BernouillyGa naar voetnoot7), que cela doit être ainsi, mais comment avez vous cru que sans cela j'eusse pu le scavoir? ou vos autres lecteurs?
Qu'il a merveilleusement reussi et aussi Jo. Bernouilly!
Ce que j'ay cherché, c'estoit principalement de voir de quelle nature estoit la courbe proposée, et si elle se pouvoit construire geometriquement ou s'il estoit besoin de supposer quelque quadrature d'une autre courbe. Ce qui s'est trouvè ainsi. Dans cette recherche j'ay remarquè quelques unes des proprietez de cette Catenaire, qui se sont ossertes. Les autres que vous ou Mr. Bernouilli avez decouvertes, je ne les ay point cherchées, comme la dimension de l'espace entre la courbe et sa base, les centres de gr. de cet espace et celuy de la courbe, parce que je [les] croiois incomparablement plus difficiles a trouver qu'elles ne sont. Je n'ay point esperè aussi que la quadrature de la courbe xxyy=a4-aayy dont j'ay dit que la construction de la chainette depend, estoit reduisible à la quadrature de l'hyperbole, a la quelle vous et Mr. Bernouilly avez reduit vostre construction, ce qui me paroit le plus beau de tout ce que vous avez tous deux decouvert.
Il est a souhaiter ce que vous dites que Mr. Bernouilly en fasse voir le rapportGa naar voetnoot8) je voudrois aussi qu'il adjoutast les demonstrations, ou manieres de trouver.
Bernoulii theorema 1, 3, 5, 6, 7, 8, 9, 10, 11 ex meis facile deducunturGa naar voetnoot9) et pleraque velut
| |
| |
corrolaria, quartumGa naar voetnoot10) non inveni, sed quomodo inventum sit non difficulter perspexi. Illud vero ne quidem quaesiveram. DuodecimumGa naar voetnoot11) ex eodem sundamento haberi poterat, cujus etiam constructio brevior Bernouliana erit, si tantum AL ponatur aequalis GK, sic enim fit L centr. gr. curvae EBF; quod se non puto ignorasse. Estque inventio centri gr. spatij CA (C) in tua figura. afsinis admodum istiGa naar voetnoot12). Spatii BAOEGa naar voetnoot13) dimensionem non habet Bernoulius ex qua etiam dimensio spatij MPO deducitur.
Il n'a rien non plus de la surface du conoide.
Je ne trouve aucune erreur ni dans vos inventions ni dans les sienes. apres les avoir toutes examinées.
Car horsmis la reduction de la construction a la quadrature de l'hyperbole, ou au Logarithmes, je vois les fondements de tout ce que vous et Mr. Bernoully avez de plus que moy; mais cette reduction, que j'estime fort, je ne vois pas jusqu'icy comment vous y estes parvenus, et vous me ferez plaisir de me l'apprendre. Quand je considere que vous avez tous deux rencontrè cette reduction, je dis qu'il faut que ce soit ou quelque stupiditè qui m'empesche de la voir, ou de ce que je suis beaucoup moins versè que vous et luy en ce qui regarde les quadratures, et comment les unes dependent des autres; ce qui est certain; ou de ce qu'on n'y peut arriver que par vostre nouveau calcul duqnel dans tout le reste je ne vois pas encore la necessitè; mais je veux croire qu'il sert a faire remarquer plus facilement les diverses proprietez des lignes qu'on examine, parce que je vois que Mr. Bernoully aussi bien que vous Mr. a deconvert des choses touchant cette chainette, que je ne me suis pas proposees à chercher, parce que je les croiois trop eloignées; mais a vous et luy il semble qu'elles se soient offertes.
J'ay souvent considerè que les lignes courbes que la nature presente souvent a nostre vue, et qu'elle decrit, pour ainsi dire, elle mesine, renferment toutes des proprietez sort remarquables. Telles sont le cercle que l'on rencontre partout. La parabole, que decrivent les jets d'eau. L'ellipse et l'hyperbole, que l'ombre du bout du stile parcourt et qu'on rencontre aussi ailleurs. La cycloide qu'un clou qui est dans la circonference d'une roue decrit. Et enfin nostre chainette qu'on a remarquée par tant de siècles sans l'examiner. De telles lignes meritent à mon avis qu'on se les propose pour exercice, mais non pas celles qu'on forge de nouveau seulement pour y emploier le calcul geometrique. C'est pourquoy je ne voudrais pas m'amuser à poursuivre ces differentes natures de chaine que Mr. Jo. Bernouilly propose, comme devant achever et pousser plus avant cette speculation.
Pour ce qui est de la courbure du ressort dont Mr. J. Bernoully fait mention elle merite d'estre recherchée, puis que c'est encore une des lignes que la Nature decrit. Mais malaisement trouvera 't on icy des principes aussi seurs, que ceux qui servent a la speculation de la chaine. Il parle en suite de la courbe que produit une voile tendue par le vent, comme estant d'une meditation tres sublime. Et il ajoute qu'une partie de la voile qui a sa soustendante perpend.re a la direction du vent doit se plier en arc de cercle, ce qui me paroit si faux que je veux plutost croire que je n'entens pas bien sa proposition que de luy imputer une erreur si grossiere.
| |
| |
1 Septembre 1691.
Monsieur
Peu de jours apres que jeus receu vostre lettre du 24 Jul. l'on m'apporta les Acta de Leipzich de May et Juin, où je vis avec bien du plaisir outre vos inventions touchant la Catenaria, les quelles vous veniez de me communiquer, celles de Mr. Jo. Bernouilly. Je vous admiray tous deux, et vous, Monsieur, surtout, d'avoir si bien reussi à decouvrir les proprietez de cette courbe, et ayant examinèGa naar voetnoot14) vos constructions et vos Theoremes, je trouvay que tout quadroit ensemble, comme aussi avec ce que j'ay donnè, en ce que nous avons de commun et qu'il n'y avoit aucune erreur. Je consideray ensuite pourquoy plusieurs de vos decouvertes m'estoient echappées, et je jugeay que ce devoit estre un effet de vostre nouvelle façon de calculer, qui vous offre, à ce qu'il semble, des veritez, que vous n'avez pas mesme cherchées, car je me souviens que dans une de vos lettres precedentesGa naar voetnoot15), vous m'aviez dit, en parlant de ce que vous aviez trouvè touchant la Catenaria, que le calcul vous offroit cela comme de soy mesme, ce qui certainement est fort beau. Pour moy je puis dire que j'ay trouvè tout ce que j'ay cherchè et plus, mais je n'ay point cherchè ni vostre dimension de l'espaceGa naar voetnoot16),
ni les deux centres de gravitèGa naar voetnoot17), n'ayant pas esperè qu'ils fussent trouvables. Ainsi ils me sont echappez, quoyque j'en aye estè fort pres. Car j'ay assez reconnu, en examinant vos theoremes là dessus, par quelle voie j'y aurois pu parvenirGa naar voetnoot18) et que ces theoremes ont une mesme origine. J'ay aussi remarquè en passant que Mr. BernouillyGa naar voetnoot19), pour avoir le
| |
| |
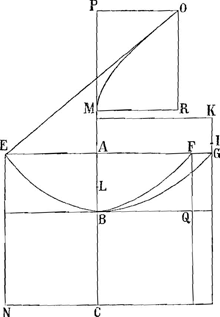
centre de gravitè L de la courbe EBF, au lieu qu'il prend BL egale à IK, n'avoit qu'à prendre AL egale à GK, et qu'ainsi le rectangle de GA, AL est tousjours egal à l'espace hyperbolique Ga naar voetnoot20) BGA. Par où il auroit encore facilement trouvè le centre de gravitè de l'espace EBF, ou, qui vaut autant, de vostre espace AONC Ga naar voetnoot21).
Ses propositions 1, 3, 5, 6, 7, 8, 9, 10, 11Ga naar voetnoot22) sont en partie les mesmes et en partie aisées à deduire des choses que j'avois trouvées, en estant comme des corollaires, quoy qu'il y en ait de fort jolies, dont peut-estre je ne me serois jamais avisè. Pour ce qui est de la surface du ConoideGa naar voetnoot23), je vois qu'il n'en dit rien, ni vous, Monsieur, touchant la courbe dont la Catenaria s'engendre par evolution, apparemment parce que vous n'y avez pas songè. Apres ma dimension
| |
| |
de l'espace BMOE, et la vostreGa naar voetnoot24) de l'espace BEA dans la 2e fig. de Mr. BernoullyGa naar voetnoot25) l'on peut aussi trouver celle de l'espace MOR, que la courbe MO retranche du rectangle MPOR, lequel espace devient egal au rectangle FC, lorsque BA est egal à RM ou BCGa naar voetnoot26), mais qu'a-t-on à faire, direz vous, de chercher si avant!
J'avois fait tout cet examen, et les remarques dont je viens de parler sans beaucoup de peine, et dès les premiers jours, mais je n'ay pu trouver la Reduction de la construction de la Courbe à la quadrature de l'Hyperbole, et c'est ce qui m'a fait differer de vous faire response. Car cette reduction me paroissant fort belle, parce qu'elle donne la maniere de trouver avec facilitè des points dans la courbe, j'aurois estè bien aise d'en decouvrir auparavant la methode par ma propre meditation, qui, à dire vray, a estè interrompue par plusieurs affaires et distractions de
| |
| |
toute sorteGa naar einda). Ensin je n'y vois point de jour encore, et puisque Mr. Bernoulli aussi bien que vous, a reussi en ce point, j'en conclus qu'il faut que vostre nouveau calcul vous ait conduit tous deux, ou bien une plus grande connaissance que vous vous estes acquise, l'un et l'autre, en ce qui est des quadratures et leurs relations et dependances mutuelles. J'ay recherchè la dessus ce que je me souvenois d'avoir vu dans les oeuvres posthumes de Mr. FermatGa naar voetnoot27), mais ce Traité est imprimè avec tant de fautes, et de plus si obscur, et avec des demonstrations suspectes d'erreur, que je n'en ay pas scu profiter. Vous me ferez donc tres grand plaisir, Monsieur, si vous me voulez donner quelque lumiere en cecy, ce que peut-estre vous pouvez en fort peu de paroles. J'avois reduit cette construction, comme vous scavez, à la dimension de la Courbe xxyy=-aayy+a4Ga naar voetnoot28) et je vois maintenant quel espace hyperbolique est
egal à un espace de cette courbeGa naar voetnoot29), mais je ne scay pas comment j'aurois pu trouver cela; et il se peut que vostre Reduction est fondée sur autre chose, ce que je seray bien aise d'apprendre. Si Mr. Bernoully en examinant le raport entre nos inventions (ainsi que vous le souhaitez) vouloit en mesme temps expliquer les fondemens de ses decouvertes, il ne seroit pas besoin que vous prissiez la peine de m'instruire, et il m'aideroit par là a entendre vostre calculus differentialis, dont je commence avoir grande envie; mais peut-estre il nous fera attendre encore longtempsGa naar voetnoot30).
Je ne voudrois jamais m'amuser à ces differentes natures de chaines, que Mr. Jo. BernouillyGa naar voetnoot31) propose comme devant achever ou pousser plus avant cette
| |
| |
speculation. Il y a de certaines lignes courbes que la nature presente souvent à nostre vue, et qu'elle decrit pour ainsi dire elle mesme, lesquelles j'estime dignes de consideration, et qui d'ordinaire renferment plusieurs proprietez remarquables, comme l'on voit au Cercle, aux Sections coniques, à la Cycloide, aux premieres ParaboloidesGa naar eindb) et à cette Catenaria. Mais d'en forger de nouvelles, seulement pour y exercer sa geometrie, sans y prevoir d'autre utilitè, il me semble que c'est difficiles agitare nugas, et j'ay la mesme opinion de tous les problemes touchant les nombres. Calculis ludimus, in supervacuis subtilitas teritur, dit quelque part Seneque en parlant de certaines disputes frivoles des philosophes Grecs.
Pour ce qui est de la courbure du Ressort, dont l'autre Mr. Bernouilly fait mentionGa naar voetnoot32), elle peut meriter quelque attention estant encore une de ces lignes que la nature decrit quoyque je doute fort si on trouvera des Principes aussi surs que ceux qui servent à la speculation de la Chainette. Il parle outre cela de la courbe que produit une voile tendue par le vent, comme estant d'une meditation tres sublime. En quoy je veux croire que je n'entens pas ce qu'il veut dire, parce que cette courbure en arc de cercle, qu'il donne à une partie de la voile, me paroist trop absurde (en l'interpretant simplement) pour qu'il se puisse estre trompè si grossierementGa naar voetnoot33).
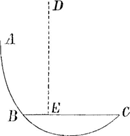
Voicy a peu pres la fig. 2e de Mr. BernouillyGa naar voetnoot34) à laquelle se rapportent les 2 remarques precedentesGa naar voetnoot35). Vous avez fort bien fait de m'advertir dans vostre
| |
| |
lettre que BC, ou bien AO dans vostre sigure doit estre la soutangente de la Logarithmique, car j'aurois eu de la peine à le deviner, et il me semble que vous en deviez informer vos lecteurs dans les Acta. Dans cette construction par la Logarithmique, qui est fort ingénieuse, la proprietè de la soutangente, que j'ay remarquée pag. 179 de mon Traitè de la LumiereGa naar voetnoot36), est venue fort à propos, car il a falu la supposer pour y parvenir si je ne me trompe.
J'espere que vous aurez trouvè du temps pour achever ce que vous m'avez promis touchant les tangentes, et je l'attens avec impatience; mais je ne souhaite pas moins d'apprendre la Reduction dont je vous ay parlè, et dont je vous auray l'obligation toute entiere. Je suis avec infiniment d'estime etc.
P.S. Je ne scay pas pourquoy ces Mrs. de Leipsich m'ont donnè cette fois le titre de Dynasta in ZulichemGa naar voetnoot37) au lieu de Zeelhem, qu'ils ont mis cy devant et qui estoit comme il faut. On pourroit croire qu'ils parlent de deux Christiani Hugenii; vous pouvez par occasion, Monsieur, les detromper. |
-
voetnoot1)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 90.
-
voetnoot2)
- Leibnizens Mathematische Schriften, Band II, p. 98 et Briefwechsel, p. 659.
-
voetnoot3)
- Ce sommaire ou cette minute se trouve à la page 121 recto et verso du livre G des Adversaria; sa rédaction diffère sur plusieurs points de celle de la lettre elle-même; ainsi nous avons cru utile de la reproduire ici.
-
voetnoot4)
- Il s'agit de la solution de Leibniz du problème de la chaînette, citée dans la note 1 de la pièce No. 2681.
-
voetnoot5)
- C'est-à-dire la raison de K à S de la note 4 de la Lettre No. 2688.
-
voetnoot8)
- C'est-à-dire le rapport entre les diverses solutions. Allusion à la remarque de Leibniz de la Lettre No. 2688: ‘j'espère que Mr. Bernoully fera une plus exacte comparaison’.
-
voetnoot10)
- ‘Spatium funicularium BAE (voir la figure de la présente lettre) vel BAF est aequale rectangulo sub BA et AF, diminuto rectangulo sub CB et FG’. Voir d'ailleurs le § I de l'Appendice No. 2694.
-
voetnoot11)
- ‘Si ad AG applicentur duo Rectangula AI, AK, quorum unum AI ei quod sub semilatere transverso CB et recta FG comprehenditur rectangulo, alterum AK quod ipsi spatio Hyperbolico BGA aequatur; et differentiae latitudinum KI sumatur in axe a vertice B aequalis BL, erit punctum L centrum gravitatis curvae Funiculariae EBF’. Voir encore le § III de l'Appendice No. 2694.
-
voetnoot13)
- Lisez BMOE et consultez la figure de la présente lettre.
-
voetnoot14)
- On rencontre cet examen aux pages 116 verso jusqu'à 119 recto du livre G des Adversaria, sous les dates des 5, 6 et 7 aoùt.
-
voetnoot16)
- Il s'agit de l'aire AONCA de la figure de la Lettre No. 2688. Selon Leibuiz elle est égale au rectangle sur OA et AR. Dans le § I de l'Appendice de cette Lettre, la pièce No. 2694, Huygens retrouve et démontre ce théorème.
-
voetnoot17)
- Le centre de gravité P de l'arc AC (voir toujours la sigure de la Lettre No. 2688) et le centre de gravité Q de l'aire AONCA. La construction de Leibniz de la distance OG du premier de ces centres à la droite NO diffère de celle énoncée par Bernoulli (voir la note 11 et la figure de la présente lettre) et aussi de celle de Huygens démontrée au § III de la pièce No. 2694. Elle est comme il suit: ‘Arcui AC vel AR, ordinatae BC, parametro OA inventa quarta proportionalis Oθ, addatur abscissae OB et summae dimidia OG, dabit G centrum gravitatis’. La construction de EA, et celle de Oβ, OG une sois trouvée, sont au contraire identiques avec celles démontrées par Huygens aux § III et IV de la pièce No. 2694. Toutes ces constructions sont d'ailleurs exactes.
-
voetnoot18)
- Voir la pièce No. 2694, aux paragraphes cités dans les deux notes précédentes.
-
voetnoot19)
- Il s'agit de son douzième théorème, cité dans la note 11 de la présente lettre.
-
voetnoot20)
- Consultez, pour la démonstration de ce théorème, le § III de la pièce No. 2694.
-
voetnoot22)
- Voici les théorèmes, tels que Bernoulli les avait formulés, avec l'indication, autant que possible, des théorèmes de Huygens avec lesquels ils sont identiques ou dont ils se déduisent facilement.
Remarquons d'abord que le BC de Bernoulli (voir ici et dans la suite la figure de la présente lettre) est égal au rayon de courbure r du sommet, employé par Huygens comme paramètre de la chaînette.
1. ‘Ducta tangente FD, erit AF:AD=BC:BF curvam’. Voir le théorème ‘KL:LS=CA ad AK curvam’ de la pièce No. 2624, démontré au § II de la pièce No. 2625. D'apres les notes marginales citées dans la note 1 du No. 2540, Huygens ajouta en marge de son exemplaire des Acta: ‘Idem ex meis: sed ego et hoc, nempe quod DF - AF ad AD ut AB ad BF curvam’. (Voir le théorème 2 de la IIIe partie de la pièce No. 2668).
3. ‘Curva BE vel BF aequalis est rectae AG, i.e. portiones curvae funiculariae ad axem applicatae consiciunt Hyperbolam aequilateram: insignis est hujus curvae proprietas’. ‘Idem ex meis’ (notes marg.). Le théorème, en effet, se déduit assez facilement au moyen des théorèmes (δ) et (ε) du § IV de la pièce No. 2669, en remarquant qu'on a d'après la construction indiquée: 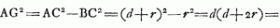 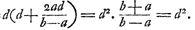 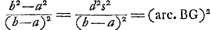 . Voir d'ailleurs le § II de la pièce No. 2694. . Voir d'ailleurs le § II de la pièce No. 2694.
5. ‘Curva MNO, ex cujus evolutione describitur Funicularia BE, est tertia proportionalis ad CB et AG’. ‘Idem ex meis’ (notes marg.). Le théorème est identique au théorème: ‘CA ad AI ut AI ad AW=CR’ de la pièce No. 2624. Voir la démonstration au § IV de la pièce No. 2625.
6. ‘Recta vero evolvens EO est tertia proportionalis ad CB et CA’. ‘Idem ex meis’ (notes marg.). Le théorème se déduit des théorèmes (δ), (ε) et (ζ) du § IV de la pièce No. 2669, en observant qu'on a 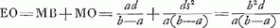 et de même: CA et de même: CA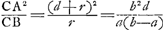 . .
7. ‘Recta BM usque ad principium curvae MNO sumta aequatur ipsi BC’. Pour la comparaison des solutions de Huygens et de Bernoulli ce théorème doit être considéré comme constituant la définition de la droite BC de Bernoulli. Huygens ajouta en marge: Idem ex meis, et insuper quod DF-FA ad FA ut AB ad BM. Voir le théorème 3 de la IIIe partie de la pièce No. 2668.
8. ‘MP est dupla ipsius BA’. ‘Idem ex meis. Verum’. (notes marg.). Ce théorème encore se déduit facilement des theorèmes (δ), (ε) et (ζ) déjà cités, en faisant usage, pour le calcul de MP, de la relation: AP:EO=AF:FD, où FD représente la tangente de la chaînette au point F.
9. ‘Rectangulum sub CB et PO duplum est spatii hyperbolici ABG’. Probablement ce numéro 9 a été ajouté par mégarde, l'annotation ‘idem ex meis’ des notes marginales y fait défaut et il n'est pas facile de voir comment ce théorème pourrait être déduit des résultats de Huygens, où la quadrature de l'hyperbole ABG n'entre en aucune manière.
10. ‘Recta CP bisecta est in puncto A’. ‘Idem ex meis’ (notes marg.). Le théorème est une conséquence immédiate des théorèmes 7 et 8.
11. Curva EB est ad curvam MNO, ut recta CB ad rectam AG’. ‘Idem ex meis’ (notes marg.). Le théorème ce déduit immédiatement des théorèmes 3 et 5.
-
voetnoot24)
- Voir la note 16 de la présente lettre. En effet, l'aire BEA se déduit immédiatement de celle dont il est question dans cette note.
-
voetnoot26)
- On rencontre ce calcul à la page 122 recto du livre G. Huygens y arrive pour l'espace MOR à la formule générale: 4/3 AG3/BC-2CA.AG+2BC. AF. Dans le cas particulier, dont il s'agit, on a:CA=2BC et AG=√CA2-BC2=BC√3 et par suite la formule se réduit à l'expression 2BC × AF=CA × AF, comme le texte l'indique.
-
einda)
- J'espere de Mr. Bernoully l'analyse par vostre methode. Trocq de Fatio.
Tschirnhaus que dit-il.
Dynasta in Zulichem [Christiaan Huygens].
-
voetnoot27)
- Voir, sur les ‘Varia Opera’ de Fermat, publiés en 1679, la note 1 de la Lettre No. 221. Il s'agit ici surtout du traité ‘De aequationum localium transmutatione et emendatione ad multimodam curvilineorum inter se vel cum rectilineis comparationem, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus’, qui occupe les pages 255-285 du Tome I de l'édition complète des ‘OEuvres de Fermat’, publiées par les soins de MM. Paul Tannery et Charles Henry, sous les auspices du ministère de l'instruction publique. Gauthier-Villars et fils, 1891. in-4o.
-
voetnoot29)
- D'après une annotation de Huygens sur la meme feuille manuscrite qui contient la minute de la pièce No. 2681, il avait trouvé que l'aire MAξθζ de la sigure de notre pièce No. 2694, devrait être le double de l'aire hyperbolique MAζ. Or, la courbe Aξθ de cette même sigure, désinie dans l'annotation mentionnée par la relation θφ=λφ2/ζφ, s'identisic, suivant le dernier alinea du § VIII de la pièce No. 2625, avec la courbe αψθ de la figure 5 de cette pièce No. 2625, c'est-à-dire avec la courbe x2y2=-a2y2+a4.
-
voetnoot30)
- En esfet, Jean Bernoulli ne publia une analyse du problème de la
chaînette qu'en 1742, dans ses ‘Lectiones Mathematicae, de methodo integralium, aliisque, conscriptae in usum Ill. Marchionis Hospitalii, Cum Auctor Parisiis ageret, Annis 1691 & 1692’.
-
voetnoot31)
- Il s'agit des chaînettes à densité inégale, mentionnées par Jean Bernoulli vers la fin de l'article, cité dans la note 1 de la Lettre No. 2681, qui contient sa solution du problème de la chaînette ordinaire.
-
eindb)
- Non pas celles cy [Christiaan Huygens].
-
voetnoot32)
- Dans l'article de Jacques Bernoulli qui parut dans les ‘Acta eruditorum’ de juin 1691, sous le titre: ‘Specimen alterum calculi differentialis in dimetienda Spirali Logarithmica, Loxodromiis Nautarum, et Areis Triangulorum Sphaericorum; una cum Additamento quodam ad Problema Funicularium, aliisque’.
-
voetnoot33)
- Voici le passage en question de l'article cité dans la note précédente: ‘Istis vero omnibus
multo sublimior est speculatio de Figura veli vento inflati; quanquam cum Problemate Funiculario eatenus affinitatem habet, quatenus venti continuo ad velum adlabentis impulsus ceu funis alicujus gravamina spectari possunt. Qui naturam pressionis fluidorum intellexerit, haud difficulter quidem capiet, quod portio veli BC, quae subtensam habet directioni venti DE perpendicularem, curvari debeat in arcum circuli. At qualem curvaturam induat reliqua portio AB, ut difficilis est perquisitio, sic in re nautica eximii prorsus usus futura est, ut praestantissimorum Geometrarum occupationem juxta cum subtilissimis mereri videatur’.
Ajoutous que l'étrange assertion de Jacques Bernoulli reposait sur la supposition que le vent ne pouvant s'echapper de la partie BC de la voile la pression y serait partout égale tandis qu'il en serait autrement pour la partie AB.
-
voetnoot35)
- C'est-à-dire les remarques sur la construction du centre de gravité de la chaînette et sur la quadrature de l'espace MOR.
-
voetnoot36)
-
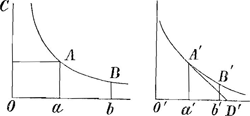
Voici la propriété en question Soit AB une hyperbole décrite sur les asymptotes Oa et OC, et A′B′ une logarithmique (y=C.e-x/k) àsoustangente constante a′D′. Alors, si Aa=A′a′; Bb=B′b′ (ou plus généralement: A′a′:B′b′=Aa:Bb), on a la relation suivante: ‘espace hyperbolique ABba: ‘parallelogramme de l'hyperbole’ OA=a′b′:a′D′
|