Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 109]

N^o 2688.
G.W. Leibniz à Christiaan Huygens.
24 juillet 1691.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et C.I. Gerhardt²⁾.
Elle fait suite au No. 2682.
Chr. Huygens y répondit par le No. 2693.

A Hanover ce 14/24 de Juillet 1691.

Monsieur

Il y a plusieurs semaines, que je Vous ay écrit de Wolfenbutel, que j'y avois receu vostre lettre avec la solution de la ligne catenaire enfermée dans une lettre pour Messieurs de Leipzig, et que je n'avois pas manqué de la leur faire tenir. Depuis j'ay attendu à vous écrire de nouveau jusqu'à ce que j'ay receu le tout imprimé dans leur mois de Juin, ou vous trouverés, Monsieur, vostre solution avec celle de Monsieur Bernoulli et la mienne³⁾. J'ay pris plaisir de voir qu'on s'est rencontré. Cela nous asseure de ne nous estre pas mépris au moins dans le fonds; il est vray que je n'ay pas eu le loisir de faire une comparaison exacte, neantmoins ayant vû, que plusieurs conclusions s'accordoient, j'en juge autant des autres, ou s'il y a quelque faute (quoy que je n'en aye point remarquée) il ne sera pas difficile de la redresser. J'ay aussi cherché quelques uns de vos cas particuliers par mon calcul, et il m'est venu la meme chose. Ainsi je m'imagine qu'il y a de l'accord. J'espere que Monsieur Bernoulli fera une plus exacte comparaison; et comme il employe ma methode, je prends part à ce qu'il a fait. Luy et moy nous avons reduit le probleme à la quadrature de l'Hyperbole, nous avons donné tous deux non seulement les tangentes et l'extension de la courbe, mais aussi le centre de gravité de la courbe, et moy j'y ay adjouté le centre de gravité de l'espace. Nous avons donné tous trois les tangentes et l'etendue de la courbe. Mons. Bernoulli s'est rencontré avec vous Monsieur à penser à la courbe dont l'evolution sert à descrire la ligne catenaire, et il a remarqué la dessus de fort jolies choses. De sorte qu'il me semble, qu'il a tres bien fait. Cependant il estoit bien eloigné, il y a deux ou

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 87.

2) Leibnizens Mathematische Schriften, Bd. II, p. 95 et Briefwechsel, p. 652.

3) Voir, sur ces trois solutions, la pièce N^o. 2681, note 1.

[p. 110]

trois ans, de se promettre quelque chose de cette nature, avant qu'il s'est façonné à mon calcul, comme il avoue luy même.

Avec tout cela ses constructions sont fort differentes des miennes. Car il se contente de supposer la quadrature de l'Hyperbole ou l'extension de la courbe parabolique, et moy j'ay reduit le tout aux Logarithmes, tant parce qu'ainsi tout vient d'une maniere tres simple et tres naturelle (tellement que la courbe catenaire semble estre faite pour donner les Logarithmes) que parce qu'ainsi je puis trouver par la Geometrie ordinaire une infinité de points veritables, ne supposant qu'une seule proportion constante une fois pour toutes, qu'on ne scauroit donner jusqu'icy Geometriquement que par l'etendue d'une courbe, ou quelque chose de semblable, au lieu qu'autrement on est obligé à chaque point de la courbe qu'on demande de recourir aux voyes extraordinaires.

Ne scachant point, Monsieur, si vous avés deja receu le mois de Juin de Leipzig,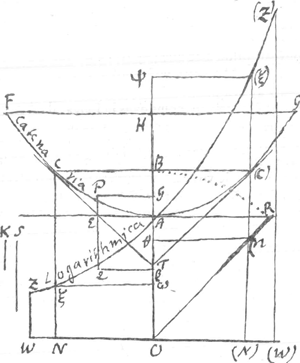



je mettray ici l'abregé de mon discours en peu de mots. FCA (C) G la catenaire, et Z ξ A (ξ) (Z) la Logarithme. On prend AO et ZW en raison S et K⁴⁾, constante et perpetuelle, une fois pour toutes les lignes catenaires et pour tous leur points. Faisant OW=O(W)=AO. Et puisentre AO et WZ, item entre AO et (W)(Z)(supposant(W)(Z) AO et WZ en progression Geometrique continuelle) on met pour ordonnées comme Nξ ou (N)(ξ) autant de moyennes proportionnelles qu'on veut; pour decrire la courbe logarithmique ZξA (ξ) (Z). Or posant ON et O(N) egales, NC ou OB ou OR est moyenne arithmetique entre Nξ et (N) (ξ) (dont la moyenne Geometrique est AO parametre de la catenaire). Ainsi la courbe cate-

4) Comme on verra dans la note 6 de cette lettre, la raison S:K=0A:ZW n'est autre que le nombre e, base du système des logarithmes népériens.

[p. 111]

naire se construit fort bien par les Logarithmes, et si elle se suppose construite par le moyen d'une chainette, elle sert à donner les Logarithmes sans calcul, ex dato numero, ou bien numeros ex dato Logarithmo⁵⁾. Voicy le reste des proprietés je suppose OR=OB et que G, P, Q sont les centres de gravité de CA (C), AC, AONCA. OR-AR=Nξ, OR+AR=(N) (ξ). Triangula OAR et CBT sunt similia (ou bien EAT); AR=AC; ψω=CA (C)=bis AC. Rectang. RAO=Spat. AONCA; Oθ:OA∷BC:AR, Oθ+OB=bis OG==quater Oβ; et AE=GP=βQ.

Je n'ay pas expliqué quelle doit estre la proportion de K à S ou de WZ à OA; mais vous jugerés aisement, Monsieur, qu' AO doit estre egale à la soustangentiale (comme vous l'appelés) de la logarithmique, et que par consequent, posant OW=AO, la raison de AO à WZ est toujours la même et determinée⁶⁾. Ainsi toutes les logarithmiques aussi bien que toutes les catenaires sont semblables ou d'une mesme espece.

J'ay donné encor quelque chose dans le mois precedent, ou j'ay redressé quelques fautes⁷⁾ de mon vieux essay de resistentia medii; j'ay aussi rendu justice à vôtre series pour l'Hyperbole qu'on a eu tort de dire la même avec celle que j'avois donnée autre fois⁸⁾. Je me suis aussi servi de l'occasion pour expliquer la ligne loxodromique, ou des rumbes par les logarithmes⁹⁾, ce que j'avois trouvé

5) Consultez, sur ces constructions et sur les théorèmes divers qui vont suivre, la solution de Leibniz, citée dans la note 1 de la pièce N^o. 2681, où ils se trouvent exposés plus explicitement.

6) Posant OA=a, O(N)=x, (N)(ξ)=y, on a, d'après la désinition de Leibniz y dx/dy=a, d'où il suit y=ae^x/a. C'est donc là l'équation de la logarithmique Z(Z) qui a servi à la construction de la chaînette et, puisque OW=a, on a OA:WZ=a:ae^-1=e:1.
Quant à la chaînette elle-même, la construction NC=½(Nξ+(N)(ξ)) amène immédiatement son équation analytique bien connue y=½ a (e^a/x+e^-a/x). Ainsi, la solution de Leibniz se distingue-t elle de celles de Huygens et de Bernoulli surtout en ce point qu'elle fait connaître presque explicitement cette équation analytique.

7) Voir, sur l' ‘Additio ad schediasma de medii resistentia’, qui parut dans les Acta d'Avril 1691, les Lettres N^o. 2659, note 4 et N^o. 2664, note 5.

8) Voir la Lettre N^o. 2636, aux pages 550 et 551.

9) Voir l'article de Leibniz des ‘Acta’ d'Avril 1691, cité dans la note 14 de la Lettre N^o. 2636. Nous reviendrons sur cet article dans une note de la lettre de Leibniz à Huygens du 21 septembre 1691.

[p. 112]

il y a plusieurs années. Mais la catenaire m'en avoit fait ressouvenir. Aussi sçait-on (ce me semble) que la chose se reduit à la somme des secantes appliquées à l'arc dont vous avés remarqué Monsieur dans vôtre solution que la catenaire depend aussi. Mons. Bernoulli y a joint aussi dans ce dernier mois, la consideration de la Loxodromique¹⁰⁾. Mais il ne s'estoit pas apperçu, que la Loxodromique se reduit à la quadrature de l'Hyperbole, ou aux Logarithmes où [ou] à la Catenaire.

Je voulois écrire il y a plus de trois semaines, pour envoyer ma solution que Mr. Fatio demande. Mais j'ay trouvé que vos lettres estoient restés à Wolfenbutel. Car comme j'y vay souvent, j'y ay un logis, où je laisse plusieurs papiers, mais les vostres y estoient restés par megarde. Et je n'ay pas voulu me hazarder sur ma memoire. Ainsi je ne puis satisfaire à ma promesse que dans quelques semaines, quand je seray à Wolfenbutel. Cependant je suis avec ardeur

Monsieur

Vostre tres humble et tres obeissant serviteur Leibniz.

10) Il s'agit d'un article de Jacques Bernoulli qui parut dans les ‘Acta’ de juin 1691 sous le titre ‘Specimen alterum calculi differentialis in dimetienda Spirali Logarithmica, Loxodromiis Nautarum, et Areis Triangulorum Sphaericorum: una cum Addimento quodam ad Problema Funicularium, aliisque, per I.B.
Ajoutons que l' ‘Additamentum’, mentionné dans le titre, contient une extension du problème de la chaînette à quelques cas où la densité varie suivant une loi connue et au cas où la chaînette est supposée extensible.