Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 95]

N^o 2681.
Christiaan Huygens aux éditeurs des Acta Eruditorum.
Appendice au No. 2680.
5 mai 1691.

La minute se trouve à Leiden, coll. Huygens.
La pièce a été publiée dans les Acta Eruditorum¹⁾.

^a) Clarissimis et Eruditione conspicuis Viris Actorum Eruditorum auctoribus Lipsiae.

Si Catena CVA suspensa sit ex filis FC, EA utrinque annexis, ac gravitate carentibus, ita ut capita C & A sint pari altitudine, deturque angulus inclina-

1) Dans la livraison de juin 1691, page 281, à l'exception toutefois du dernier alinéa, et avec le titre: Christianii Hugenii, Dynastae in Zülechem, Solutio ejusdem problematis.
La pièce y fait suite à la ‘Solutio problematis funicularii, exhibita a Iohanne Bernoulli, Basil. Med. Cand. et à l'article: ‘De linea in quam flexile se pondere proprio curvat, ejusque usu insigni ad inveniendas quotcunque medias proportionales et Logarithmos. Auctore G.G.L.’.
Ces trois solutions sont précédées de l'avertissement suivant:

Solutiones Problematis A.J.B.

in Actis A. 1690. p. 219 propositi.

‘Benevolus Lector haud gravate recordabitur Problematis a Clarissimo Basileensium Professore Jacobo Bernoulli, Actorum anno 1690, mense Majo p. 219, propositi. Hujus solutionem, methodo sua impetratam, si ante anni exitum nemo solutum a se Problema significaverit, se publicaturum ejusdem anni mense Julio p. 360, pollicitus est celeberrimus G.G.L. Solvit vero illud, solutionemque nobis communicavit praeterito mense Decembri proponentis Frater, Dominus Joannes Bernoulli, Medicinae Candidatus, in hisce studiis versatissimus; eamque, ut suo tempore alteri illi Leibnitianae jungeremus, humanissime per Fratrem nos compellavit. Factum inde est, ut Virum supra memoratum celeberrimum pulsaremus de edenda sua: quam etiam nuperrime nobis pro summa humanitate sua transmisit. Huic etiam debemus quod vir summus Dn. Christianus Hugenius non dedignatus est, cum plurima favoris ergo nos significatione, & sua Problematis dicti solutione Acta haec nostra exornare. Exhibemus ergo Tibi B.L. & geminam solutionem ab Illustri Virorum pari, & Bernoullianam; sed eo ordine quo ad manus nostras pervenere’.

a) Hasce inclusi literis eodem die ad Leibnitzium datis [Cht. Huygens].

[p. 96]

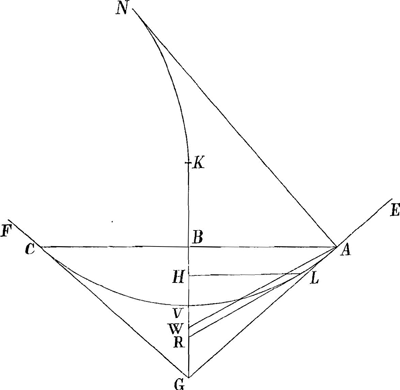
tionis filorum productorum CGA, & catenae totius positus, cujus vertex sit V, axis VB.

1. Licebit hinc invenire tangentem in dato catenae puncto²⁾. Veluti si punctum datum sit L, unde ducta applicata LH dividat aequaliter axem BV. Jam si angulus CGA sit gr. 60. erit inclinanda a puncto A ad axem recta AW, aequalis 3/2 AB, cui ducta parallela LR, tanget curvam in puncto L. Item si latera GB, BA, AG sint partium 3, 4, 5, erit AW ponenda partium 4½.

2. Invenitur porro & recta linea catenae aequalis vel datae cuilibet ejus portioni³⁾.

Semper enim dato angulo CGA, data erit ratio axis BV ad curvam VA.

Velut si latera GB, BA, AG sint ut 3, 4, 5, erit curva VA tripla axis VB.

3. Item definitur radius curvitatis in vertice V, hoc est semidiameter circuli maximi qui per verticem hunc descriptus totus intra curvam cadat⁴⁾. Nam si

2) Consultez la sousdivision (γ) du § IV de la pièce N^o. 2669. En effet, il résulte de la page 108 recto du livre G. qui porte la suscription: ‘missa ad auctores actorum Lipsiensium 5 Maj 1691’, que les résultats numériques qui suivent, ont été calculés au moyen de la formule AW=eb-ea/d+a, qui se retrouve vers la fin de la sousdivision mentionnée. Dans cette formule on a: a=AB, b=AG, d=BV, e=HV.
Ajoutons que les numéros 1-6 de la présente pièce correspondent avec les mêmes numéros de la le et de la IIIe partie de la pièce N^o. 2668.

3) Voir la sousdivision (δ) du paragraphe cité dans la note précédente. D'après cette sousdivision on a: arc AV=s/b-a BV, où s=BG.

4) Voir la sousdivision (ε), d'après laquelle: VK=a/b-a BV.

[p. 97]

angulus CGA sit 60 gr., erit radius curvitatis ipsi axi BV aequalis. Si vero angulus CGA sit rectus, erit radius curvitatis aequalis curvae VA.

4. Poterit et circulus aequalis inveniri superficiei conoidis, ex revolutione catenae circa axem suum⁵⁾.

Ita si ang. CGA sit gr. 60. erit superficies conoidis ex catena CVA genita aequalis circulo, cujus radius possit duplum rectangulum BVG.

5. Invenientur etiam puncta quotlibet curvae KN, cujus evolutione una cum recta KV radio curvitatis in vertice, curva VA describitur. Atque evolutae ipsius KN longitudo⁶⁾.

Velut si ang. CGA fuerit 60 gr., erit KN tripla axis BV. Si vero latera GB, BA, AG sint ut 3, 4, 5, erit illa 9/4 axis BV.

6. Praeterea spatij NKVAN quadratura datur⁷⁾.

Posito enim ang^o. CGA 60 gr., erit spatium illud aequale rectangulo ex axe BV, et ea quae potest triplum quadratum ejusdem BV. Si vero latera GB, BA, AG sint ut 3, 4, 5, erit idem spatium aequale septuplo quadrato BV cum parte octava.

7. Porro puncta quotlibet catenae inveniri possunt, posita quadratura curvae alterutrius harum: xxyy ∞ a⁴-aayy vel xxyy ∞ 4a⁴-x⁴. Vel etiam data distantia centri gravitatis ab axe, in portionibus planis, quas abscindunt rectae axi parallelae in curva harum priore⁸⁾.

Quadratura autem hujus curvae pendet a summis Secantium arcuum per minima aequaliter crescentium⁹⁾: quae summae ex Tabulis sinuum egregio quodam adhibito compendio inveniuntur quamlibet proxime¹⁰⁾. Hinc ex. gratia inventum quod si ang. CGA fit rectus, et ponatur axis VB partium 10000; erit BA, 21279 non una minus. Curva autem VA per superius indicata¹¹⁾ congnoscitur bic esse partium 24142, non una minus.

5) Voir le § VI de la pièce N^o. 2625. D'après ce paragraphe, le rayon du cercle mentionné dans le texte égale √2KV × VG; où, dans le cas ∠CGA=60^o, on a, d'après le troisième théorème de la présente pièce, KV=BV.

6) Voir la note 8 de la pièce N^o. 2668 et la sousdivision (ζ) du § IV de la pièce N^o. 2669. D'après cette sous-division on a KN=ss/a(b-a) BV.

7) Voir le § V de la pièce N^o. 2625, d'après lequel l'aire en question est égale à l'expression: ½ arc. VA × VK+⅙ arc. VA × KN, d'où les résultats numériques qui vont suivre se déduisent facilement au moyen des formules mentionnées dans les notes précédentes.

8) Consultez la 11^e partie de la pièce N^o. 2668, à laquelle cette première partie de ce numéro 7 correspond.

9) Voir le § I de la pièce N^o. 2634.

10) Consultez sur ce ‘compendium’ la lettre de Huygens à Leibniz du 16 novembre 1691.

11) Il s'agit du deuxième théorème de la présente pièce. On a, en effet, d'après la formule de la note 3, pour le cas présent: arc. AV=1/√2-1BV=(1+√2) BV=2,4142...BV.

[p. 98]

In his omnibus non nisi ad casus singulares solutiones problematum dedi vitandae prolixitatis studio, et quoniam non dubito quin Regulas universales Viri docti affatim sint exhibituri. Quod si tamen aliquae ex nostris requirentur, eas lubenter mittam¹²⁾. Ac jam pridem omnes apud Claris. virum G.G. Leibnitzium involucro quodam obtectas deposui¹³⁾.

Rogantur Viri Clarissimi, deque scientiarum studijs quam optime meriti, ut quae de Problemate Catenae Bernouliano pagellis hisce exposui, si digna videbuntur cum caeteris quae Eruditorum cohors suppeditabit in lucem edere velint.

Ita jam pridem non uno nomine sibi obstrictum novo officio devinciar.

Chr. Hugenium.

D. Hagae Com. 5 Maj. 1691.

12) On rencontre aux pages 128 verso et 129 recto du livre G des Adversaria le commencement d'un article, destiné pour les ‘Acta’ ou plus probablement, puisqu'il est rédigé en Français, pour l'‘Histoire des ouvrages des sçavans’. Dans cet article Huygens se proposait d'exposer ‘les voies qui (l'ont) conduit à (ses) découvertes’ sur la chaînette. Nous reproduisons cet article inachevé, qui doit avoir été composé dans les derniers mois de l'année 1691, à la fin de la correspondance de cette année.

13) Voir les Lettres N^o. 2623, du 9 octobre 1690, et N^o. 2667, du 26 mars 1691.