Oeuvres complètes. Tome IX. Correspondance 1685-1690
(1901)–Christiaan Huygens–
[pagina 541]
| |||||||||||||
No 2634.
| |||||||||||||
§ I.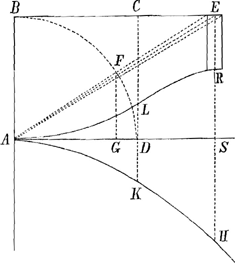 AKH hyperbola aequilatera, centro B, semi axe BA. BE perp. AB. ut et AS. HE parall. AB. Proportionales sunt HE, SE, RE. Item KC, DC, LC, et ita ubique. et curva ALRGa naar voetnoot2). [Jam si sit in fig. pag. 14a, ut WX ad XS, ita hic BE ad BA. Erit ibi longitudo catenae VSPA ad rectam AZ, sicut hic ▭ BS ad spatium ALREB]Ga naar voetnoot3). Triangulum minimum FA est ad ▭ minimum ER in ratione composita ex Δo FA ad Δo EA et ex Δo EA ad ▭ ER. Hoc est in rat. compos. ex rat. qu. AF, ad qu. AE et rate SE ad 2RE. Est autem RE=FG sinui compl.i anguli EAB, quia HE = AE et quia prop.les HE, SE, RE ut et AE, ES, FG. | |||||||||||||
[pagina 542]
| |||||||||||||
Dicatur AF, r. AE, s; FG seu RE, c. Ergo ratio triang.i seu sectoris minimi
adeoque sector totus FAB ad spatium ERLABE sicut radius multiplex per numerum integrorum omnium graduum arcu FB contentorum ad duplam summam omnium secantium graduum integrorum usque ad secantem AE inclusiveGa naar voetnoot4). | |||||||||||||
§ II.BVZ est hyperb. aequilatera centr. A vertice B. AD et BC perpend. AB. 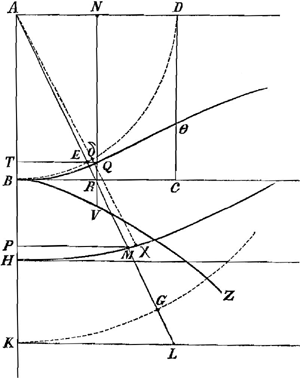 | |||||||||||||
[pagina 543]
| |||||||||||||
VN, RN, QN proportionales, et sic ubique. Curva est BQθGa naar voetnoot5) per puncta sic inventa. BD quadrans peripheriae centro A. Eam secat RA in E. ET perp. AB. Jam est AT = NQ et TEQ recta lineaGa naar voetnoot6). Ostensum est pag. 17a in fineGa naar voetnoot7), sectorem ABE esse ad spatium ABQN sicut radii omnes sectoris ABE, arcum BE in particulas aequales dividentes, ad duplam summam omnium secantium, arcubus aequaliter per istas particulas crescentibus convenientium. Sicut autem secans earum quaevis dupla ut LA (posita nempe AK = 2AB et KL perp.i ÀK) ad radium EA, ita triangulum minimum MAX (sumpta MA media prop.i inter LA, EA, vel inter GA, RA; quia GA dupla EA, et RA dimidia LA) ad triangulum minimum EAδ, seu sectorem minimum. Ideoque si totus sector BAE ita in sectores minimos aequales divisus intelligatur et simul eorum radiis continuatis spatium AHM in triangulos minimos. Erit omnes isti sectores minimi ad omnia haec triangula minima, hoc est totus sector ABE ad spatium AHM, ut omnes radii sectorem ABE dividentes ad omnes duplas secantes ipsis convenientes, hoc est ut sector idem ABE ad spatium ABQN. Ideoque spatio huic aequale erit spatium AHM. Fit vero et spatium BTQ aequale spatio HPM, quia triang. APM = rectang.o TN, ut facile demonstratur. Si AP sit x:PM = y. AB = a, fit 4a4 - x4 = xxyyGa naar voetnoot8) aequatio curvae HM. Si AN sit x:NQ = y, fit a4 - aayy = xxyy, aequatio curvae BQθ, quarum quadratura unius a quadratura alterius pendet. AH med. prop. AK, AB. AP, AH, AM semper sunt proportionales. quia 4a4 = xxyy + x4, unde xx + yy ad 2aa ut 2aa ad xx, et √xx + yy∶√2aa ut √2aa∶x, hoc est MA ad HA ut haec ad AP. |
|