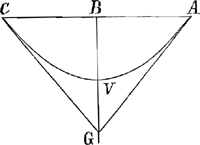
Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 63]
| |||||||||||||||||||||||||||||||||||||||||||
No 2669.
| |||||||||||||||||||||||||||||||||||||||||||
§ IGa naar voetnoot2).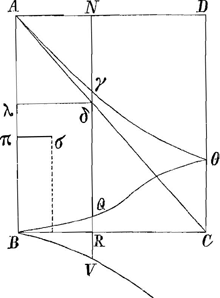 Fig. 1.
BQθ est curva pag.ae praecedentisGa naar voetnoot3), altera nempe ex iis quae ad catenariae constructionem requiruntur. Altera est Aγθ. Dico spatium prioris BQNA ad spatium posterioris AγN esse ut AB ad πσ distantiam centri gravitatis spatii BQNA ab recta AB. Adeo ut si detur hoc centrum gr. non opus est quadratura spatii AγN, neque ipsius spatii consideratione (ad inveniendam scilicet rationem AB ad BV axem catenae, est enim BV ipsi πσ aequalis)Ga naar voetnoot4). Quia enim ut VN ad RN ita RN ad QNGa naar voetnoot5), itemque ut VN ad RN ita δN ad γNGa naar voetnoot6). Erit RN ad QN ut δN ad γN. Quare | |||||||||||||||||||||||||||||||||||||||||||
[pagina 64]
| |||||||||||||||||||||||||||||||||||||||||||
γN ducta in RN aequabitur QN ducta in δN, sive in δλ. idque ubique: Ergototum spatium AγN suspensum ex brachio librae quod aequale sit AB, aequiponderabit spatio ABQN ut jacet ponderanti super axem AB: sive eidem spatio ex centro grav. suae σ suspenso, et ex distantia σπ ponderanti. Ergo spatium ABQN erit ad spatium AγN, ut AB distantia ad distantiam σπ. (Sed spatii AγN quadratura opus est ad inveniendum longitudinem curvae AV quia per illam quadraturam inventum est quod ut diff.a AR-AB ad BR ita est BV ad curvam AV. Item ad alia utilis est eadem quadratura, quam postea inveni, vid. pag. 82 et 87)Ga naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||
§ IIGa naar voetnoot8).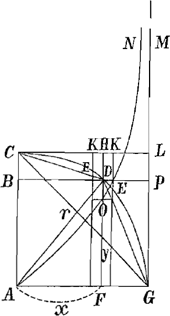 Fig. 2.
ACG circuli quadrans. CLG A quadratum; à puncto peripheriae D cadunt in AG et AC perpendiculares DF, DB.
Hujus curvae spatium infinitum AONMG, aequale est quadrato CG. Item spatii ejus portio ut OAF, est ad rectangulum FC, ut BC ad BD. | |||||||||||||||||||||||||||||||||||||||||||
[pagina 65]
| |||||||||||||||||||||||||||||||||||||||||||
(Sive spatium OAF est aequale ▭o BL ut facile apparet ex calculo)Ga naar voetnoot10). Quia enim AD ad DF ut particula curvae minima EDE ad KK, erit AD seu HF ducta in KK=DF ductae in EE. idemque pars superficiei cylindricae ex KK circa AG, aequalis parti superficiei sphaericae ex EE circum eandem AG. Unde (ut notum est) tota superficies cylindrica ex CL circa AG aequalis superficiei sphaericae ex arcu CDG circa AG. Porro quia superficies ex EE circa AG ad supersiciem ex eadem EE circa CA, sicut DF ad DB, erit et superficies ex KK circa AG, ad superficiem ex EE circa CA, ut DF ad DB, hoc est, ex constructione, ut HF ad FO; atque ita tota superf. cylindrica ex CL circa AG ad superficiem sphaericam ex arcu CDG circa CA, ut omnes HF ad omnes OF, hoc est ut quadratum CG ad totum spatium infinitum AONMG. Est autem ostensum superf. cyl. ex CL circa AG aequalis superficiei sphaericae ex arcu CDG circa AG, ideoque et superficiei sphaericae ex arcu CDG circa CA, quia utraque dimidiae sphaerae superficiei aequalis est. Ergo ratio superficiei ex CL circa AG ad superf. sphaericam ex arcu CDG circa CA erit ratio aequalitatis, ac proinde et ratio qu.i CG ad spatium infinitum AONMG erit aeqalitatis, quod erat dem.m. Porro ex ratione demonstrandi, patet etiam superficiem cylindricam ex CH circa AF, sive ex arcu CD circa AF esse ad superficiem ex eodem arcu CD circa CB, ut rectangulum HA ad spatium curvae OFA; atqui ex Archimede est superf.s ex CD arcu circa AF ad surperf.m ex eodem arcu CD circa CB sicut excessus quadrati CG supra qu. GD ad quadr. ex CD recta, hoc est sicut excessus AG supra GF, seu sicut AF aut BD ad BC. Ergo et rectang.m HA ad spatium OFA ut BD ad BC, quod erat dem. | |||||||||||||||||||||||||||||||||||||||||||
§ IIIGa naar voetnoot11).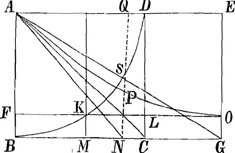 Fig. 3.
Ulterior disquisitio circa catenae curvam ex animadversa quadratura curvae APOE quae pag. 20 erat δθ.
| |||||||||||||||||||||||||||||||||||||||||||
[pagina 66]
| |||||||||||||||||||||||||||||||||||||||||||
ex proprietate curvae ad catenam: aaxx-aayy=xxyy pag. 20Ga naar voetnoot12)
aa/b = FK; ex a=FL et a - aa/b = KL; aa - a3/b = ▭ MD=sp. AOF ex proprietate curvae pag. 58Ga naar voetnoot13) quae est eadem atque illa pag. 20 mutatis reciproce x in y, unde et illa pag. 20 quadraturam recipit, quod nunc demum animadversi.
Item spat. AOE ad spat. APQ ut AG-AB ad NA-AB. | |||||||||||||||||||||||||||||||||||||||||||
§ IVGa naar voetnoot14).Sit AV catena pendensGa naar voetnoot15). AG tangens in A. angulus BAG=BAG in 1a fig. | |||||||||||||||||||||||||||||||||||||||||||
[pagina 67]
| |||||||||||||||||||||||||||||||||||||||||||
(α) Jam divisam ponendo catenam AV [2a fig.] in particulas aequales, earum summa est ad VZ ut totidem radii ad sinus omnes complimenti in arcu SB [1a fig.] qui pertinent ad totidem tangentes aequaliter crescentes in recta BG. Item summa particularum aequalium catenae AV est ad AZ sive BV, ut totidem radii ad sinus omnes in arcu SB qui ad easdem illas tangentes pertinent. Hoc utrumque pag. 14 ostenditurGa naar voetnoot16). 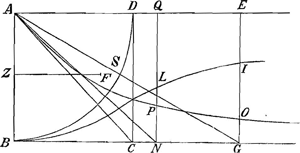 Fig. 4.
1a fig. 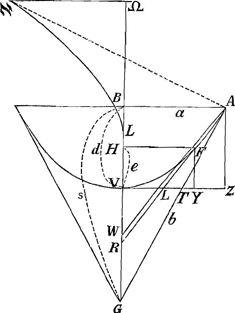 Fig. 4.
2a fig. (β) Porro sicut curva AV, recta VZ, et recta AZ, ita sunt inter se ▭ BE [1a fig.], spatium ABIE, et spatium APOE. Hoc explicatur pag. 20 et 14Ga naar voetnoot17). | |||||||||||||||||||||||||||||||||||||||||||
[pagina 68]
| |||||||||||||||||||||||||||||||||||||||||||
Quia ut AV, VZ, ZA, sunt summae totidem radiorum, totidem sinuum complimenti, et totidem sinuum, pro angulis quorum tangentes aequaliter sese exedunt; ita quoque ▭ BE, spatium ABIE, et spatium APOE, quando ang. AGB utrobique est idem.
(γ) Habeat BV [2a fig.] ad VH, sive AZ ad FY rationem datam, (puta duplam), sitque FR tangens in F. Et secetur spatium APOE recta NPQ, ut sit spatium APOE ad spat. APQ ut BV ad VH; dico angulo ANQ esse aequalem angulum tangentis HFR. Est enim YF ad ZA ut summa sinuum (summa nempe sinuum qui pertinent ad angulos quorum tangentes sese aequaliter excedunt, quod de his omnibus sinibus ita est intelligendum) usque ad angulum FLY seu HFR, ad summam sinuum usque ad angulum ATZ seu GAB, sed ut YF ad ZA, seu ut HV ad VB, ita quoque spatium APQ ad sp. APOE. Ergo summa sinuum usque ad angulum HFR ad summam sinuum usque ad ang. GAB sicut spat. APQ ad spat. APOE; hoc est sicut summa sinuum usque ad ang. ANQ ad summam sinuum usque ad ang. AGE sive GAB, in 1a fig. vel etiam in 2.da. Ergo summa sinuum ad usque ang. HFR aequalis est summae sinuum adusque ang. ANQ; ideoque ang. HFR aequalis ang.o ANQ, quod erat dem. Si AB, BG in utraque fig.a magnitudine sibi respondeant, erunt et AG aquales, et AN aequalis AW, cui tangens FR parallela ducenda est. Si AB=a. AG=b, fit spatium APOE=ab-aa, vid. pag. 82Ga naar voetnoot18). Si BV=d. VH=e. Et ut d ad e ita faciendum spatium APOE ad sp. APQ. Sit AN=x. Ergo spat. APQ=ax-aa. Ergo
Hinc problema de invenienda quavis tangente, per unam AG datam. p. 83Ga naar voetnoot19). | |||||||||||||||||||||||||||||||||||||||||||
[pagina 69]
| |||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||
[pagina 70]
| |||||||||||||||||||||||||||||||||||||||||||
§ VGa naar voetnoot26).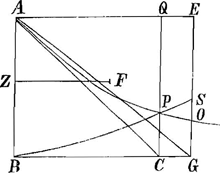 Fig. 5.
fig. 1a 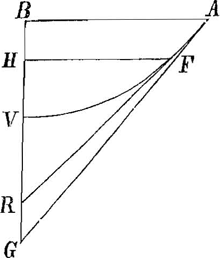 Fig. 5.
fig. 2da AB=3 BG=4 GA=5
Quaeritur VH et HF definientes punctum F, cujus tangens FR inclinetur ad BR angulo semirecto. Sit in fig. 1a ABCQ quadratum, et GB ad BC ut 4 ad 3 sintque curvae ut supraGa naar voetnoot27) BPS, APO. Jam ut spat. AOE ad spat. APQ, ita est BV [fig. 2da] ad VHGa naar voetnoot28). Hoc est ut 2 ad 3√2-3 sicut ostenditur initio pag. hujusGa naar voetnoot29) quia spatia sunt ut GA-AB [fig. 1a] ad CA-AB, vid. pag. 82Ga naar voetnoot30). Sic quidem dato vertice V [fig. 2da] invenitur punctum H, atque etiam F, dato catenae positu. Sed nec punctum V potest inveniri nisi approximatione quadraturae vel ope distantiae centri gr.isGa naar voetnoot31) portionis BSEA ab AB, quae in hac catenae positione AV est prox. 601Ga naar voetnoot32) partium qualium AB 1000 nec rursus punctum F nisi ex cognita per ejusmodi approximationem ratione inter HV, HF quae est proxe ut 46996Ga naar voetnoot33) ad 100000. | |||||||||||||||||||||||||||||||||||||||||||
[pagina 71]
| |||||||||||||||||||||||||||||||||||||||||||
Ex charta crassa (carton) figura ABSEA abscindatur, postquam curva BPS inscripta fuerit: invenitur autem facile per puncta ex libello sinuum; nam posita tangente BG cujuslibet anguli BAG, erit ES sinus compl. anguli ejusdemGa naar voetnoot34). Figurae resectae ABSEA centr. gravitatis mechanice inveniatur F. Erit jam in catena pendente fig.a 2da, si angulus BGA quem facit tangens in A, aequalis sit ang.o BGA in fig. 1a, ratio applicatae in catena ad axem ejus BV, sicut in fig. 1a AB ad ZFGa naar voetnoot35). Sic inveni, si AB applicata sit 1000 partium AG 5000, unde BG 4900Ga naar voetnoot36), fore BV=1720 prox. Si AB sit 1000. BG 2446, tunc AB, BV fore aequales. Si AB 1000. sintque AB, BG, GA ut 3, 4, 5; fore BV=601. Si AB 1000, AG 2000, ut in triango aequilatero, fit BV=763. Si AB 1000, itemque BG; fit BV=469. Sed accuratâ supputatione si fuerit hic AB 10000, fit BV=4699Ga naar voetnoot33). Quoniam charta illa non prorsus aequalis est ubique crassitudinis, melius ex linteo uno, vel pluribus conglutinatis, ipsoque glutine duratis ac dein levigatis figurae rescinderentur. Parata figura una longiore, quaelibet breviores ex ipsa in aliam chartam circumscribi possunt, quarum exscissarum centrum gr. inveniatur. |
| ||||||||||||||||||||||||||||||||||||||||||


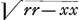
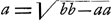 :
: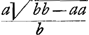
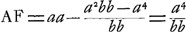 , qu.FK,
, qu.FK,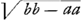 =AE;
=AE;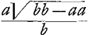 =AF;
=AF;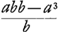 =▭FE
=▭FE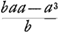 =sp. AOF
=sp. AOF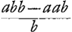 =ab-aa=sp. AOE.
=ab-aa=sp. AOE.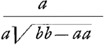 (▭ BE): ab-aa (spat. AOE)=√bb-aa(AE):(b-a) (SG)
(▭ BE): ab-aa (spat. AOE)=√bb-aa(AE):(b-a) (SG)