Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 59]

N^o 2668.
Christiaan Huygens.
1691.
Appendice I au No. 2667¹⁾.

La pièce se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek²⁾ et C.I. Gerhardt³⁾.

Chifre envoiè à Mr. Leibnitz le 26 Mars 1691⁴⁾ et à Mr. De Beauval⁵⁾ le 27 Mars.

1) Cet Appendice contient l'explication de l'anagramme de la Lettre N^o. 2667, telle qu'elle se trouve aux pages 93 verso et 94 recto du livre G des Adversaria. On l'a divisée en trois parties et, à l'exemple d'Uylenbroek, mis en regard les anagrammes avec les explications, lesquelles, dans le manuscrit de Huygens, se trouvent écrites à la suite des premiers.

2) Christiani Hugenii etc. Exercitationes Mathematicae, Fasc. II, p. 83.

3) Briefwechsel, p. 644.

4) Voir la Lettre N^o. 2667.

5) Nous ne connaissons pas la lettre de Huygens à Basnage de Beauval. La communication n'a pas été insérée dans l' ‘Histoire des Ouvrages des Sçavans’, rédigée par cet auteur.

I^e Partie.

	s.c.a.p.s.s.e.f.ae.u.a.g.c.q.c.s.i.e.a.	Si catena ad parietem suspensa sit ex filis aequalibus, utrimque annexis, gravitate carentibus, quarum capita sint in eadem altitudine, deturque angulus inclinationis filorum et catenae positus^6):
	d.a.i.f.e.c.p. hae 7 literae desunt in Leibnitziano, additae in Beauvallino.
1.	p.i.t.i.d.q.c.p.	Possumus invenire tangentem in dato quolibet catenae puncto^7);
2.	r.ae.c.v.c.e.p.	rectam aequalem catenae vel cuilibet ejus portioni;
3.	r.c.i.v.	radium curvitatis in vertice.

6) A propos des mots en italiques, Huygens a ajouté plus tard l'annotation suivante: hoc oblitus eram in illo quod ad Leibnitsium, addidi in eo qd. ad Beauvallium.

7) Les numéros 1 à 6 de cette première partie et ceux de la troisième correspondent de telle manière que les résultats annoncés dans la première sont donnés explicitement au même numéro de la troisième partie.

[p. 60]

4.	c.ae.s.c.e.r.c.c.a.	circulum aequalem superficiei conoidis ex revolutione catenae circa axem;
5.	c.e.l.l.c.e.c.c.d.	constructionem et longitudinem lineae, cujus evolutione curva catenae describitur^8);
6.	m.s.c.e.p.c.	mensuram sectoris cui evoluta pro centro.

8) Ce numéro fait exception à la règle de la note précédente pour autant que la construction de la développée n'est pas indiquée expressément au numéro correspondant de la troisième partie de cette pièce, mais la rectification une fois obtenue, cette construction est facile, puisque p.e. KR=AC+CR (voir la figure de cette pièce).

II^e partie.

p.c.i.p.p.q.c.a.h. xxyy=a^4-aayy xxyy=4a^4-x^4.	Puncta catenae inveniri possunt posita quadratura curvae alterutrius harum: xxyy=a^4-aayy^9), xxyy=4a^4-x^4^10);
v.d.d.c.g a.a.i.p.c.p. Hoc in gryphis quos dedi deest.	(vel data distantia centri gravitatis ab axe in portionibus curvae prioris^11). hoc in gryphis quos dedi Leibnitzio et Beauvallio non est additum sed postea per literas^12) ad Leibnitsium misi.

9) Voir le § VIII de la pièce N^o. 2625.

10) Voir la pièce N^o. 2634.

11) Voir la sousdivision γ de la pièce N^o. 2669.

12) Voir la Lettre du 21 avril 1691 de Huygens à Leibniz.

III^e partie.

1.

s.u.a.c.t.a.p.a.q.i.a.e.d.c.p.e.v., i.s.t.i.c.c.^13) a.a.q.^14) i.a.a; e.e.h.c.ae.i.a.c.c.a.a.; h.i.p.a.p.d.d.t.c.i.i.h.p.

Si, ut axis catenae totius ad partem axis quae inter applicatam ex dato catenae puncto et verticem, ita sit tangens in capite catenae^15) ad aliam, quae huic ipsi applicatae addatur; et ex his compositae aequalis inclinetur a capite catenae ad axem^16), huic inclinatae parallela a puncto dato ducta, tanget curvam in ipso hoc puncto. vid. pag. 87^17).

13) Plus tard, Huygens a indiqué dans une note marginale que l'on doit intercaler ici les lettres d s a, en ajoutant: ‘haec omissa in missis ad Leibn. et Beauvallium’.

14) On doit de même intercaler ici la lettre h représentant le mot huic, lequel également, comme le prouve l'inspection du manuscrit, a été ajouté après coup.

15) Plus tard Huygens intercala ici les mots: ‘demta sua applicata’, en ajoutant ‘hoc omissum in eo quem ad Leibnitsium misi et ad Beauvallium’.

16) Il s'agit de la ligne AW (voir la 2^a fig. de la figure 4 de la pièce N^o. 2669) qu'il faut prendre égale à VH(AG-AB) / VB+AB.

17) Voir la sousdivision γ du § IV de la pièce N^o. 2669. En effet, la construction indiquée se déduit facilement de la formule finale de cette sousdivision.

[p. 61]

2.	u.t.i.c.c., d.a., e.a.a., i.s.a.d.c.l.	Ut tangens in capite catenae, demta applicata, est ad axem, ita subtangens ad dimidium catenae longitudinem. vid. p. 82 et 87^18).
3.	a.i.q.a.a.r.c.i.v.	Atque ita quoque applicata ad radium curvitatis in vertice. vid. ibidem^19).
4.	s.c.c.e.c.r.c.a.ae.e.c.c.r.e.m.p.i.d.r.c.i.v.e.p.a.q.i.v.e.t.	Superficiei curvae conoidis ex catenae revolutione circa axem aequalis est circulus cujus radius est medius proportione inter duplum radium curvitatis in vertice et partem axis quae inter verticem et tangentem. vid. pag. 16^20).
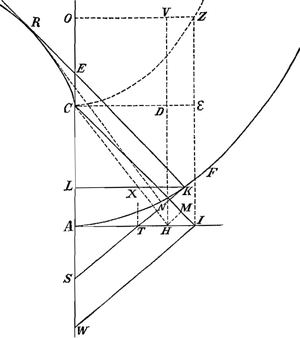
5.	u.r.e.a.e.d.i.t.e.a.a.q.s.i.r.c.i.v.^21) a.c.c.e.c.d.	Ut rectangulum ex applicata et differentia inter tangentem et applicatam ad quadratum subtangentis, ita radius curvitatis in vertice^22) ad curvam cujus evolutione catena describitur. vide pag. 17^23) ubi patet evolutam CR aequari rectae AW, positis proportionalibus CA, AI, AW. Est autem AI=curvae seu AK.

18) Voir la sousdivision δ du paragraphe cité.

19) Voir la sousdivision ε.

20) Voir le § VI de la pièce N^o. 2625.

21) Les lettres en italiques doivent être remplacées par la seule lettre a, comme Huygens l'indique en ajoutant: ‘hic error non erat correctus in eo quod ad Leibnitsium misi 26 Mart. 1691, sed in eo quod ad Beauvallium postridie misi, ita ut hic’.

22) Les mots en italiques ont été biffés depuis et remplacés en marge par le mot ‘axis’.

23) Il s'agit du § IV et de la figure 4 de la pièce N^o. 2625. Pour faciliter la lecture nous reproduisons la figure. Voir la page suivante.

[p. 62]

		Unde AW seu CR = cc/r. Est autem r seu radius curvitatis = ad/ b-a^24) ut videre est pag. 87. Itemquec=ds/b-a utibidem. Unde sit cc/r = dss/ ab-aa ut in hac 5^a proportione.
6.	s.c.e.p.c.e.ae.r.e.l.c.d.e.c.e.s.e.e.s.r.c.i.v.	Sector cui evoluta pro centro est, aequatur rectangulo ex longitudine catenae dimidia et composita ex sextante evolutae et semisse radii curvitatis in vertice. vid. pag. 17^25).

24) Voir, pour l'explication des lettres, la sousdivision ζ du § IV de la pièce N^o. 2669, laquelle en effet, se trouve à la page citée, c'est-à-dire à la page 94 verso de la pagination générale.

25) Voir le § V de la pièce N^o. 2625. En effet, la formule de ce paragraphe peut s'écrire c(⅙e+½r), où c représente la demi-longueur de la chaînette complète CVA (voir la figure de la note 1 de la pièce N^o. 2669).