Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 135]

N^o 2694.
Christiaan Huygens.
[août 1691.]
Appendice de la pièce No. 2693¹⁾.

La pièce se trouve à Leiden, coll. Huygens.

1) Cet appendice, que nous avons emprunté aux pages 119 verso et 120 recto du Livre G, contient la quadrature de la chaînette et la détermination des centres de gravité de l'arc et de l'aire d'un segment de cette courbe. Nous l'avons divisé en quatre paragraphes.

§ I²⁾.

Sit catena AV; vertex A; axis CAM; Aλ tangens in vertice; Vπ tangens in

2) Quadrature de la chaînette. On retrouvera cette quadrature, obtenue par un raisounement semblable, dans un article qui a paru dans l' ‘Histoire des Ouvrages des Sçavans’ de Février 1693 sous le titre ‘Lettre de Mr. Huygens à l'Auteur’, où Huygens est revenu sur le problème de la chaînette (voir la Correspondance de l'année 1693).

[p. 136]

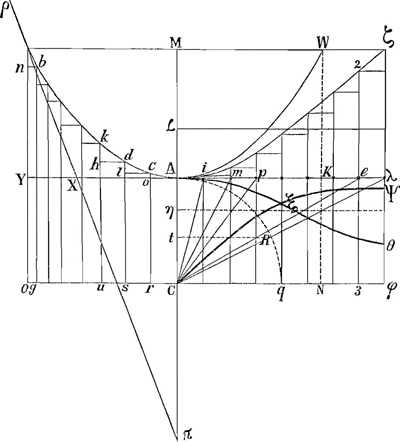
V. Sit Aλ aequ. catenae AV, et fiat angulus AλC aequ. VπA. Et divisa sit Aλ in totidem partes aequales quae sunt internodia aequalia in AV.

Ex demonstratis pag. 92³⁾, scimus angulos cAo, dcl, kdh tales esse ut tangentes eorum crescant aequaliter ut numeri 1, 2, 3, 4, etc.; cumque ulterius Vbn sit aequalis ang.^o λCA, eo quod AλC factus sit aequ. nVb, sequitur internodia Ac, cd, dk etc. inclinari ad perpendiculares seu axi MC parallelas, sicut respective inclinantur Ci, Cm, Cp, etc. ad rectam Aλ.

Porro est AV curva, seu Aλ recta, ad VY, ut ▭ Cλ ad spatium Cξψφ⁴⁾, quod aequale esse ostendimus rectang.^o CRλ⁵⁾. Ergo Aλ ad VY ut ▭ Cλ ad ▭ CRλ, hoc est ut Aλ ad λR. Ergo VY=λR. Et tota VO aequ. Cλ, nam CR=YO seu CA ex constr.^ne Eodem modo ostenditur bg aequalis Ce, atque ita de caeteris.

Notatu dignum quod spatia cC, dr, ks etc. sunt omnia inter se aequalia si portiones curae Ac, cd, dk, etc. sint aequales. Nam si has tanquam internodia recta consideremus, et tanquam radios circuli habeamus, erunt Ao, cl, dh, etc. sinus complementorum angulorum ACi, ACm, ACp, etc. eoque erunt inter se sicut sinus compl. angulorum horum in quadrante CAq; sed hi sinus in secantes istorum angulorum ducti essiciunt quadratum radii, (velut λC in Ct facit ▭ aequale qu. CR, quia λC ad CA seu RC, ut RC ad Ct). Ergo eaedem secantes ductae unaquaeque in rectas Ao, cl, dh etc. sibi respondentes, hoc est quae subjacent internodiis tantundem ab A distantibus, quantum secantes quaeque, efficient quoque rectangula acqualia inter se Ar, cs, du etc., ac singula aequalia ▭ Ar, unde sequitur spatium totum AVOC aequari rectang.^o Aφ. Unde dimensio cognoscitur spatii AMV⁶⁾.

3) Il s'agit du § I de la pièce N^o. 2625. Huygens ajouta ici en marge: ‘Imaginandum internodium, horizonti parallelum, esse minimum respectu caeterorum’.

4) Voir le § VII de la pièce N^o. 2625 et surtout la note 21 de cette pièce.

5) D'après le § III et la figure correspondante de la pièce N^o. 2669, on a: spat. AOE=a(b-a), où a=AB, b=AG. En appliquant ce résultat à notre figure, on trouve:spat. Cξψφ==AC×(Cλ-AC)=CR×Rλ. Huygens, plus tard, annota ici en marge: ‘hac tamen quadratura nihil opus erat’. En effet, il n'était pas difficile de montrer que les accroissements successifs de la diagonale Cλ égalent partout ceux de l'ordonnée Vy, comme par exemple Cp-Cm=kh (parce que kd=mp et ∠hkd=∠mpC), donc Vy=λR; ce qu'il fallait prouver. C'est la voie suivie dans l'article cité dans la note 2.

6) Pour démontrer l'identité de ce résultat avec celui annoncé par Bernoulli et que nous avons cité dans la note 10 de la Lettre N^o. 2693, nous n'avons qu'à remarquer que, d'après le § III de la pièce N^o. 2625, le triangle AIC de la figure 4 de cette pièce est cougruent avec le triangle AλC de notre figure, puisque AI, comme Aλ, égale l'arc de la chaînette et que CI, comme Cλ, représente une perpendiculaire à la tangente. Il s'ensuit done que l'AC de notre sigure s'identisie avec le rayon de courbure du sommet de la chaînette, c'est-à-dire, comme nous l'avons vu dans la note 22 de la Lettre 2693, avec la ligne BC de la figure de Bernoulli, reproduite dans la même Lettre. Mais on a dans notre figure:spat. AMV=▭ OM - spat. AVOC=▭ CW - ▭ Aφ=▭ AW - ▭ Nλ=AM×MW - AC×Kλ, ou bien, dans la figure de Bernoulli, BA×AF-CB×FG, puisque AG y égale l'arc de la chaînette.

[p. 137]

§ II⁷⁾.

Si super Cφ erigatur perpend.^s ρζ aequalis Cλ, ieu OV, constat punctum ζ esse in hyperb.^a aequilatera Aζ, cujus centrum C, semidiameter CA, vertex A. Similiterque si statuatur 3^e2 aequ. Ce, hoc est bg, etiam punctum 2, esse in eadem hyperbola. Unde liquet, descripta ejusmodi hyperbolâ Aζ, si ad eam producatur applicata catenariae quaelibet VM, fore Mζ applicata in hyperbola, aequalem curvae interceptae VA, quod invenit Jo. Bernoulius.

7) Vérification du troisième théorème de Bernoulli. (Voir la note 22 de la Lettre N^o. 2693).

§ III⁸⁾.

Ad inveniendum centrum grav. curvae AV, cogitandum e medio singulorum internodiorum aequalium Ac, cd, dk, etc. rectas axi parallelas cadere in CO parallelam tangenti AY. Et quoniam hae rectae onerantur singulae pondere aequali unius internodii, facile intelligitur centrum gr. curvae AV tantum distare ab OC recta, quanta est summa omnium earundem rectarum divisa per numerum ipsarum. Sed eaedem rectae sunt erectae super Cφ in hyperbolico spatio AζφC,secantes nempe in duo aequalia singulas partes in recta Cφ acceptas, atque aeque magnas iis quae sunt in vatena AV; ac porro patet quod si ▭ Lφ ponatur aequale spatio AζφC, summa rectarum totidem, in eo rectangulo, iisdem divisionibus rectae Cφ insistentium, aequalis erit summae dictae rectarum in spatio AζφC, ac proinde quoque summae rectarum in spatio ACOV. LC vero est aequalis summae rectarum in ▭ Lφ divisae per numerum ipsarum. Ergo eadem LC aequalis quoque summae rectarum spatii ACOV divisae per ipsarum numerum; ac proinde aequalis distantiae centri gr. curvae AV ab recta CO⁹⁾.

Distantia autem centri gr. curvae AV ab MA est AX, si X sit intersectio tangentium curvae in V et A; quia si catena AV obrigescere ponatur, eo nihil mutatur figura ejus; tunc vero intersectio filorum ρV, λA curvam AV sustinentium necessario cadet in perpendicularem per ejus centrum grav. transeuntem. Ergo et antequam rigesceret.

8) Détermination du centre de gravité de l'arc de la chaînette.

9) Remarquons encore que la construction, indiquée dans la Lettre N^o. 2693 à la page 130, se déduit facilement du résultat obtenu ici. Puisque, en effet, ▭ Lφ=AζφC, il suit immédiatement ▭ Lζ=AζMA, c'est-à-dire, dans la figure de la page 130, ▭ LG=BAGB.

[p. 138]

§ IV¹⁰⁾.

Porro facile quoque ipsius spatii VAW centr. gr. invenitur; quod nempe cognoscitur ex centro gr. spatii VACO. Hoc autem datur ex eo quod rectangula omnia minima Ar, cs, du etc. sunt inter se aequalia et centra gr. singulorum in mediis earum altitudinibus. Hinc enim sicut summae omnium rectarum a mediis internodiis Ac, cd, dk in CO cadentium, aequabatur summa totidem rectarum in spatio hyperbolico AζφC aequaliter distantium; ita summa omnium e centris gr. rectangulorum Ar, cs, du etc., in CO cadentium, aequabitur dimidio summae istarum rectarum in spatio hyperbolico AζφC; hoc est summae partium istarum rectarum quae sunt in ▭ ηφ, si hoc aequale ponatur ½ spatii AζφC, sive ½ ▭ Lφ. Et summa illarum e centris gr. rectangulorum Ar, cs etc. in CO cadentium per numerum ipsarum divisa, quae dat distantia gravitatis spatii AVOC ab recta CO, aequabitur summae harum rectarum in ▭ ηφ per ipsarum numerum divisae, hoc est ipsi rectae ηC, quam apparet dimidiam esse CL, quia ▭ ηφ dimidium fecerimus ▭ Lφ.

Denique perspicuum est spatii AVOC distantiam centri gr.¹¹⁾ esse eandem AX quae et curvae AV, cum rectanguli Ar, cs, du sint aequalia sicut internodia ipsis respondentia Ac, cd dk etc.

10) Détermination du centre de gravité du segment V AW de la chaînette, comme aussi de la figure VOCA.

11) Intercalez ici ‘ad CM’.