|
| |
| |
| |
No 2695.
Christiaan Huygens à G.W. Leibniz.
4 septembre 1691.
La lettre se trouve à Hannover, Bibliothèque royale.
La Minute se trouve à Leiden, coll. Huygens.
La lettre a été publiée par P.J. UylenbroekGa naar voetnoot1) et par C.I. GerhardGa naar voetnoot2).
Elle fait suite au No. 2693.
G.W. Leibniz y répondit le 21 september 1691.
Hofwijck à la Haye ce 4 Septembre 1691.
Monsieur
Il y a 3 jours que je me donnay l'honneur de vous escrire une assez longue lettre. A peine une demie heure apres que je l'eus envoiée à la poste, je trouvay avec plaisir ce que jusques là je n'avois pu penetrer, scavoir la Reduction de la Construction de la Catenaria à la quadrature de l'Hyperbole, de sorte que je souhaitois fort de faire revenir ma lettre pour y adjouter cela, mais comme je demeure icy à ma maison de campagne, à une lieue de la Haye, le courier auroit estè parti devant que j'eusse pu contremander celuy que j'en avois chargè. Je n'ay donc pu m'empescher de vous escrire cette autre, non seulement pour vous epargner la peine de me montrer ce qui en cecy m'avoit semblè trop difficile, comme je vous en avois priè, mais aussi pour vous faire voir la Construction qui m'est venue, asin que je puisse scavoir si je n'ay pas tenu la mesme route que vous, Monsieur, dans cette recherche; ce que je croiray estre ainsi, si j'apprens que vous ayez rencontrè la mesme construction, devant que d'aller à la vostre par les Logarithmes. C'est une merveille comment quelque fois en un clin d'oeil on s'apperçoit de ce qu'on n'a sçu voir auparavant quoy qu'en estant fort proche.
J'avoue qu'il y a eu du hazard et du bonheur à mon egard, et c'estoit beaucoup de sçavoir que la chose estoit possible: c'est pourquoy j'admireray d'autant plus vostre methode, si elle vous a conduit d'abord à faire cette decouverte, aussi bien que Mr. Bernoulli, sans que vous sçussiez rien l'un de l'autre, quant à ce point de recherche. Ma construction est telle: que CS, RV se coupent à angles droits en B, qui soit le sommet de la Chainette, BC le parametre, à qui soit prise egale BM.
| |
| |
Pour trouver la longueur de quelque appliquée AE à un point A dans l'axe, il
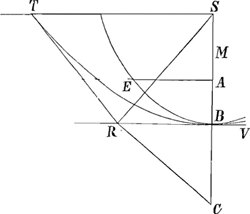
faut mettre CR egale à CA, et sur CR mener la perpendiculaire RS, qui rencontre l'axe en S. Puis appliquer ST à angles droits à l'axe BS de la Parabole BT, dont le sommet soit B, le foier M. Alors, si de la courbe parabolique BT on oste la droite RS, ou bien RT, qui est tangente de la parabole en T, le reste sera egal à l'appliquée AE Ga naar voetnoot3). Cette construction differe beaucoup de celle de Mr. Bernoullij sans que je me puisse imaginer pourtant, par quelle autre voie la siene a estè trouvée hors celle que j'ay suivie.
Ce seroit une belle chose qu'une methode pour connoitre, quand l'equation d'une Courbe est donnée, si sa dimension se peut reduire à celle de l'Hyperbole ou du Cercle, et j'avois cru que vous et Mr. Bernoullij aviez eu quelque telle invention. C'est ce qui m'a fait faire bien du chemin en vain, sans m'appercevoir
| |
| |
du veritable, qui est fort beau et sans beaucoup de detour, comme je crois que vous le scavez fort bien.
Avant hier me vint voir icy le Sr. WeigeliusGa naar voetnoot4), professeur à Jena, qui m'entretint
| |
| |
de ses grands desseins pour l'avancement des sciences et qui paroit extremement satisfait de certaines demonstrations qu'il pretend avoir de l'existence de Dieu et de la Providence. Je l'iray voir à la Haye, où il dit avoir un coussin rempli de ressorts et autres curiositez qu'il veut me montrer. Il dit qu'il a l'honneur de vous connoitre, depuis le temps que vous estudiez en mathematiques sous luy. J'aimerois bien mieux voir icy son disciple, a qui je suis etc.
Monsieur
Tres humblement
P.S. Devant que de fermer cette lettre, j'ay considerè les paroles de Mr. Bernoully, dans ce qu'il a donnè dans les Acta, touchant la Catenaria, où il dit: Hujus autem et praecedentis Constructionis demonstr ationem lubens omitto, ne Celeberrimo Viro primae inventionis palmam vel praeripiam, vel inventa sua super hac materia plane supprimendi ansam praebeamGa naar voetnoot5). D'où il semble qu'il avoit envoiè ses decouvertes à Mrs. de Leipsich pour vous estre communiquées. Car si son intention eust estè qu'elles fussent tenues secrettes, jusqu'à la publication generale, comment vous pouvoit il praeripere palmam primae inventionis, (de quoy il a cru se garder en ne decouvrant pas ses deux demonstrations) ou vous donner sujet de supprimer vos inventions. Je veux croire pourtant, puis que vous m'en assurezGa naar voetnoot6), Monsieur que vous n'avez point vu la construction de Mr. Bernoully, devant que de donner la. vostre; mais il se pourroit qu'il seroit venu à vostre connaissance (puis que le memoire de Mr. Bernouilly estoit à Leipsich depuis le mois de Decembre et qu'il n'en avoit pas recommandè le secret) qu'il l'avoit à la quadrature de l'hyperbole; ce qui me paroist d'autant plus vraisemblable, que l'invention de cette construction ne semble pas dependre de vostre methode, mais d'une remarque particuliere qui ne s'offre pas facilement d'elle mesme. Il est vray aussi que lorsqu'au mois d'Octobre 1690Ga naar voetnoot7) vous me racontastes sommairement vos decouvertes touchant cette courbe, vous adjoutiez supposita ejus constructione, de sorte que vous n'aviez pas encore alors cette construction. Vous auriez pu prevenir tous ces doutes, qui en tout cas ne vous peuvent pas faire grand tort, en donnant
| |
| |
vos inventions sous la couverture du chifre, comme je vous l'avois conseillè plus d'une foisGa naar voetnoot8). |
-
voetnoot1)
- Christiani Hugenii etc. Exercitationes mathematicae, Fasc. I, p. 94.
-
voetnoot2)
- Leibnizens Mathematische Schriften, Band II, p. 101, et Briefwechsel p. 663.
-
voetnoot3)
- Après le préambule: ‘Inveni 1 Sept. 1691, momento post quam ad Leibnitsium literas dedissem in quibus querebar hactenus non potuisse me hoc invenire, nempe constructionem Catenariae ex data mensura lineae Parabolicae, vel quadratura Hyperbolae’, on rencontre à la page 123 verso du livre G quelques figures peu achevées et quelques phrases détachées, qui toutefois permettent de reconstruire avec sûreté l'artifice dont Huygens s'est servi pour arriver à la construction décrite dans le texte de cette lettre et que l'on retrouvera d'ailleurs dans l'article de février 1693, cité dans la note 2 de la pièce No. 2694.
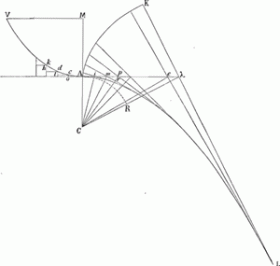
Pour l'exposer ici en peu de mots, nous commençons par reproduire une partie de la figure de la pièce No. 2694, pour la description de laquelle nous renvoyons à cette pièce, tout en y ajoutant quelques lignes nouvelles AK, AL, etc. empruntées aux figures de la page citée du Livre G. Ensuite nous remarquons que les petits triangles rectangulaires de la partie droite de la figure, tels que mpr, seront congruents avec les triangles, tels que khd, distribués le long de la chaînette, comme cela résulte de la note 5 de la pièce No. 2694, puisque dk=mp et ∠ hkd=∠ mpr. Pour trouver l'appliquée VM de la chaînette, onn'aura donc qu'à sommer les côtés, tels que mr, de ces petits triangles.
Or, si l'on prolonge ces côtés, ils envelopperont une certaine courbe AL, qui n'est autre qu'une parabole ayant A pour sommet et C pour foyer, puisqu'en effet ces côtés ne diffèrent pas sensiblement des perpendiculaires, érigées aux divers points de la droite Aλ sur les rayons vecteurs, tels que Cm, partant du point C; mais alors il est clair que la somme de tous ces côtés égale la ligne Kαl, où K représente un point de la développante AK de la parabole AL.
On a donc VM=Kλ=KL-Lλ=arc. AL-λL, tandis qu'en même temps Rλ==Σpr=ηk=AM; donc CM=Cλ.
Ces indications sussiront pour expliquer les constructions du texte, puisqu'elles mènent directement à celle donnée en seconde ligne, d'après laquelle AE (voir la figure du texte)
= arc BT-RT tandis que l'autre se déduit facilement à l'aide des propriétés bien connues de la parabole.
-
voetnoot5)
- Ces paroles s'appliquent aux deux constructions de la chaînette, indiquées par Bernoulli, dont la première suppose la quadrature de l'hyperbole et l'autre, comme celle de Huygens, la rectification de la parabole.
|



