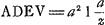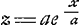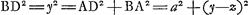Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 407]

N^o 2793.
Christiaan Huygens à H. Basnage de Beauval.
[février] 1693.

La pièce a été imprimée dans l'Histoire des Ouvrages des Sçavans¹⁾.

Je vous envoye Monsieur la construction d'un Probleme, qui sans doute plaira aux Geometres, si vous prenez la peine de la leur communiquer, étant fort belle, & ayant quelque chose de singulier. Elle m'a été envoyee par Monsieur le Marquis de l'Hospital²⁾, qui fait honneur à ces sciences, & qui me fait juger par cet échantillon, & par quelques autres que j'ay vus de luy, qu'il ne cede en rien aux plus savants Geometres de ce tems. Je vous envoye aussi à cette occasion quelques unes de me dernieres speculations en des matieres assez semblables.

Le Probleme de Monsieur le Marquis est de trouver une ligne droite egale à une partie donnée de la ligne Logarithmique. Il se sert avec adresse, pour en

Fig. I.

trouver la solution, du Calculus differentialis du celebre Monsieur Leibnitz, & la reduit à la quadrature d'une Courbe dont l'Equation est a⁶ ∞ aaxxyy+y⁴xx:x & y etant les inderterminees qui font un angle droit³⁾. Laquelle quadrature il fait voir qu'elle depend de celle de l'Hyperbole⁴⁾; donnee, comme on fait, en supposant la Logarithmique decrite. Sa construction revient à cecy⁵⁾ (Fig. I). Soit la logarithmique indefinie ACD, son Asymp-

1) Dans le fascicule de décembre 1692, janvier et février 1693, p. 244-257 au ‘Mois de Février’. 's Gravesande en a donné une traduction latine dans ses ‘Chr. Hugenii Opera Varia’, p. 507.

2) Voir les Lettres N^os. 2760, 2765 et 2775.

3) Consultez la Lettre N^o. 2765 à la page 315, où le problème est réduit à la sommation des a²dy:y√a²+y², c'est-à-dire, dans la conception de Huygens, à la quadrature de la courbe x=a³:y√a²+y².

4) Voir la Lettre N^o. 2775.

5) Ce qui va suivre est identique avec la construction simplifiée, communiquée par Huygens à de l'Hospital dans sa Lettre N^o. 2777.

[p. 408]

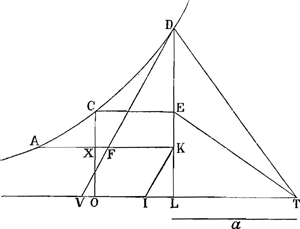
tote LO, sa soutangente perpetuelle donnee a Et la portion de la courbe soit CD, a laquelle il faille trouver une ligne droite egale.

Il faut mener DL, CO perpendiculaires à l'Asymptote, CE perpendiculaire a DL, & prenant LT dans l'Asymptote, égale à la soutangente a, & joignant les droites TD, TE, faire TV égale à TD, & TI égale à TE. Puis ayant joint VD, luy mener parallele IK, & de K, où elle rencontre DL, mener KA parallele à l'Asymptote, coupant DV en F, CO en X, & la logarithmique en A. Alors les droites AX & FK, prises ensemble seront égales à la courbe CD.

La solution du même Probleme, à ce que je trouve, se peut aussi reduire à la quadrature d'une courbe, dont l'Equation est a⁴ ∞ xxyy-aayy⁶⁾, laquelle depend, comme l'autre, de la quadrature de l'Hyperbole, comme je pourrois le prouver par une demonstration assez aisée⁷⁾. Mais la construction aboutit à la même que je viens de raporter.

Je ne say s'il y a beaucoup de lignes courbes qui ayent cette propriété, que leur longueur se puisse mesurer par elles mêmes. Cependant en voicy une que j'ay rencontrée il n'y a pas long-tems⁸⁾; qui, comme vous verrez, est encore digne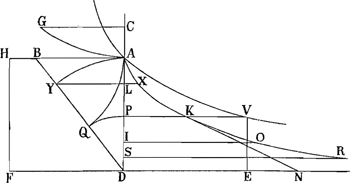

Fig. II.

d'être remarquée pour autre chose. C'est (Fig. II) la courbe AXKO, étenduë à l'infini le long d'une droite qui est son Asymptote, DN; à laquelle AD, tangente au sommet A, est perpendiculaire, & dont la proprieté principale, & très-simple est, que toute tangente, entre le point de contact et l'Asymptote, comme KN, est égale à la ligne AD. Elle s'étend encore de même de l'autre côté de cette perpendiculaire AD. Pour trouver une droite égale à une portion donnée de cette courbe depuis le sommet A, comme AK, (car par là on l'aura aussi pour toute autre portion) il faut mener KP perpendiculaire sur AD, & ayant decrit un arc de cercle PQ, ayant D pour centre, & pour demidiametre DP, trouver en AB parallele à l'Asymptote, le point B, qui soit centre de la circonference qui passe par A, & touche l'arc PQ, ce qui est aisé. En suite ayant

6) Voir la Lettre N^o. 2777 à la page 349.

7) Voir la pièce N^o. 2778.

8) Le 29 octobre 1692; voir le § I de l'Appendice N^o. 2794 à la présente lettre.

[p. 409]

mené la droite BD, il faut prendre sur elle DY, egale à DA, & du point Y mener une parallele à l'Asymptote, jusques á la courbe en X. alors cette YX sera égale à la courbe AK⁹⁾. Et la nature de cette ligne est telle, que quand on prend des proportionelles autant qu'on veut dans la droite AD depuis D, comme DS, DI, DP, & qu'on mene les appliquées SR, IO, PK; les parties interceptées de la courbe, comme RO, OK, sont toutes égales.

Elle sert encore à la quadrature de l'Hyperbole. Car la même droite YX fait avec AD un rectangle égal à un espace hyperbolique ADEV, terminé par AD, VE, perpendiculaires sur FDE, une des Asymptotes, lesquelles perpendiculaires sont dans la raison de AD à DP; l'Hyperbole AV étant Equilatere, & son quarré à l'angle des Asymptotes étant ADFH. D'où l'on voit reciproquement comment on peut trouver les points de cette courbe, en supposant la quadrature de l'Hyperbole.

Elle a encore d'autres proprietez remarquables, comme sont que l'espace infini entre la courbe, l'Asymptote, & la droite AD, est égal au quart du cercle dont AD est demidiametre¹⁰⁾. Que le solide infini, que produit cet espace en tournant sur l'Asymptote, est égal au quart de la sphere du même demidiametre¹¹⁾. Que la surface de ce solide infini, sans la base, est égale au cercle dont le demidiametre est la diagonale du quarré sur AD¹²⁾.

Mais ce n'est pas pour tout ce que je viens de raporter touchant cette ligne que je la propose icy; mais pour une autre raison; qui est qu'on peut trouver moyen de la decrire par une machine assez simple, & par là reduire l'Hyperbole au quarré, ce qui m'a semblé digne de la consideration des Geometres.

La construction de la machine est fondée sur la proprieté susdite de la Tangente, & sur un principe ou loy du mouvement, qui est, que si sur un plan horizontal on tire un point, qui par son poids ou autrement fasse quelque resistance, étant joint au bout d'un fil, ou d'une verge inflexible, dont on fasse simplement avancer l'autre extremité, ce point decrit une courbe dont le fil ou verge sera toûjours la Tangente.

Dans l'instrument ou machine que je viens de dire¹³⁾, il faut mener le bout D

9) Malheureusement les manuscrits de Huygens ne contiennent que très peu de renseignements sur la manière par laquelle cette construction, dont il est d'ailleurs facile de constater l'exactitude par les procédés modernes, a été obtenue. Seulement le § II de l'Appendice N^o. 2694 nous apprend comment Huygens avait pu conclure à la possibilité d'une telle construction, la tractrice étant considérée comme tracée.

10) Voir le § IV de la pièce N^o. 2694. Ce theorème est le seul, parmi tous ceux que se rapportent ici à la tractrice, dont les manuscrits nous fassent connaître la déduction.

11) Voir le § V de la pièce N^o. 2794.

12) Voir le § VI de la pièce N^o. 2794.

13) Dès la page 117, datée du 29 octobre 1692, d'où nous avons emprunté le § I de la pièce N^o. 2694 et qui contient aussi les premières recherches géométriques sur la tractrice, jusqu'à la page 137, le livre H est rempli de divers projets d'instruments propres à décrire la tractrice. C'est d'abord sur le poids de la pièce qui porte le stylet traçant que Huygens compte pour obtenir la pression nécessaire contre la plaque sur laquelle la courbe sera tracée, et dont la situation horizontale est obtenue à l'aide d'un niveau. De cette manière il a réussi, comme il le dit sous la date du 10 novembre 1692, à décrire exactement sa Tractoria ou quadratrice de l'Hyperbole à l'aide d'un instrument qui consiste simplement en une règle reposant sur deux pointes dont l'une constitue le stylet traçant, tandis que l'autre peut tourner librement dans une cavité d'un curseur glissant le long du bord de la plaque. La règle y est lestée par un poids attaché à une lame recourbée, soudée à la règle et contournant le bord opposé de la table, de sorte que le poids se trouve sous la table, juste au-dessous du stylet traçant.
Toutefois Huygens, considérant qu'un manque d'horizontalité de la plaque aurait trop d'influence sur le tracé de la courbe, ne s'est pas arrêté définitivement à ce projet. Pour obvier à ce défaut, il cherche à obtenir une pression supplémentaire sur la pointe traçante, indépendante de la gravité. A cet effet, il imagine même un appareil dans lequel il emploie la pression de l'atmosphère. C'est une fiole renversée, telle qu'il l'employait sur le plateau de sa machine pneumatique, et dont l'embouchure armée d'un anneau métallique reposait sur une rondelle de cuir ou de papier mouillé, donnant au centre libre passage au style traçant solidement attaché à l'anneau métallique, dont il occupait le centre. A cet anneau était fixée la tige qui devait entraîner l'appareil. Un vide partiel était produit dans la fiole en chauffant préalablement l'air intérieur au moyen d'une flamme.
Cette disposition ne pouvait réussir, parce que la friction, résultant de la pression sur la rondelle, s'opposerait aussi bien au mouvement tournant de la fiole, qui est une conséquence de l'attachement rigide de la tige à l'anneau métallique, qu'au mouvement en avant dans la direction de la tige; et le passage suivant, que nous empruntons à la page 135 du manuscrit cité, montre comment Huygens s'était rendu compte que cette circonstance fausserait nécessairement le résultat obtenu: ‘Quidsi baculo AB (voir la figure de cette note) angulis rectis affixus sit CD; sint autem cuspides planum radentes in A et B, ac



trahatur extremum D secundum regulam EF. Sic punctum C non describet tractoriam nostram ut experientia docet, ac tanto minus quanto brevior CD ad AB comparata. Hinc satis apparet, nec tunc tractoriam a puncto C descriptum iri, si AHBG sit orbis cujus C centrum. Ergo nec cucurbita nec orbis planus, aut cimbula...ad hanc descriptionem conducent’.
Huygens, pour remédier à cet inconvénient, imagine d'abord de remplacer la fiole par un cylindre creux de peu de hauteur, dont le couvercle est muni en dehors d'une pointe qui passe par un petit trou dans le bras CD; mais bientôt il a recours à un autre projet qu'il désigne comme ‘optimus modus describendae quadraticis nostrae’ et qui consiste en une poulie reposant horizontalement sur son axe dont l'extrémité inférieure forme le stylet. Les deux bouts d'une corde appliquée dans la gorge de la poulie sont fixés à un point du curseur. La poulie, revêtue des deux côtés d'une ou deux rondelles de laine, est fortement pressée par une planche parallèle à la plaque horizontale, sur laquelle elle repose, et retenue à distance fixe d'elle par quatre petits pieds. Mais avec cet arrangement Huygens prévoyait encore des difficultés pour obtenir un tracé exact, surtout près du sommet de la courbe, par suite de l'impossibilité d'éviter quelque allongement de la corde à l'origine du mouvement. C'est ce qui l'amène à remplacer la corde par une tige reliant l'axe de la poulie au curseur et pouvant tourner librement par un angle droit dans une cavité de la poulie.
Ajoutons qu'incidentellement Huygens s'occupe encore d'autres dispositions; c'est une fois une charrette à deux roues, ayant un long timon dont l'extrémité est poussée le long d'une droite horizontale. A l'autre bout, au milieu entre les deux roues, le timon porte un cilindre vertical dans lequel peut glisser le stylet, qui doit tracer sur le plan horizontal la courbe en question.
Une autre fois c'est une petite nacelle en forme de portion de sphère assez plate, qu'on fait nager sur l'eau ou sur du sirop, et chargée d'un bâton qu'on pose dessus en équilibre et dont on traîne l'un des bouts en ligne droite, ou tirée par une pointe fixée au centre de la nacelle. Il est vrai qu'il serait difficile d'obtenir de cette manière un tracé de la tractrice, mais, comme Huygens le remarque, ‘l'aissieu de la nacelle, prolongè en haut et rencontrant un fil tendn sur le baquet...resoudra le problème de la quadrature hyperbolique’.

[p. 410]

du fil ou de la verge DA dans la ligne droite DN, & trouver moyen que la pointe A, qui est à l'autre bout, se tienne droite, & qu'elle presse contre le plan horizon-

[p. 411]

tal, plûtôt par ressort que par poids; parce qu'ainsi la courbe AK se decrit sans faute qui soit sensible, quoy que le plan ne soit pas exactement de niveau. Et l'on peut savoir si elle a sa veritable figure, en repoussant le bout N de la verge par la même droite ND, parce qu'il faut que la pointe repasse de K en A sur la même trace qu'elle vient de marquer¹⁴⁾.

Si cette description, qui par les loix de la Mechanique doit être exacte, pouvoit passer pour Geometrique, de même que celles des sections de Cone qui se font par les instrumens l'on auroit par elle, avec la quadrature de l'Hyperbole, la construction parfaite des Problemes qui se reduisent à cette quadrature¹⁵⁾; comme

14) Dans le manuscrit cité, Huygens insiste beaucoup sur ce point. On y lit entre autres à la page 120: ‘Palmarium quod reversione pedis secundum canonem cognoscere licet ut curva recta descripta sit an secus. Hinc enim fit ut falli non possimus’ et encore à la page 121 ‘sed praesto est examen reversionis per idem vestigium, quod hic ante exposui. Hinc enim fit ut decipi nequeamus; certiusque colligatur recte prescriptam esse curvam hanc nostram quam circino ductu circuli circumferentiam’.

15) A la page 123 du livre H on trouve encore à ce propos les remarques suivantes: ‘On ne dira jamais que les constructions des problèmes qui se font par la règle et par le compas sont imparfaites par ce qu'on y suppose un plan parfait, une règle parfaite et que d'un point à un autre on puisse tirer une ligne droite, quoyque la derniere perfection soit impossible aux hommes en ces choses; mais on se contente de scavoir que estant supposées parfaites, il n'y manqueroit rien à la justesse de la construction, et qu'on peut approcher assez pres à fabriquer une règle parfaitement droite et un plan juste, pour tirer l'utilité qu'on desire dans ce travail. Il en est de mesme dans ma construction de la quadr.re de l'hyperbole ou je suppose un plan parfait et qui soit exactement parallele à l'horizon, car ce qui entre de plus, scavoir qu'en tirant simplement par un fil on une regle un point pesant attache a leur autre bout le long d'un plan ce point suivra tousjours la direction de la ligne qui le tire, et descrira une courbe que cette ligne touchera toujours en allant, ce n'est pas une demande mais un theoreme veritable en mechanique et qu'on peut facilement demontrer. Il n'y a donc proprement que la demande d'un plan horizontal dont j'ay besoin pour la dimension de l'hyperbole. On n'y peut obtenir la derniere perfection; aussi ne peut on faire une regle droite, mais on peut faire comme à la regle ainsi à ce plan horizontal; qu'il y manque si peu, que quand il seroit tres parfait la construction ne seroit pas differente au sens de nostre vue de ce qu'elle est; ce qui s'en suit de la certitude que donne l'epreuve de retour par la courbe decrite dont j'ay parle cy-devant.
On doit avouer que ma courbe estant supposée ou donnée, on a la quadrature de l'Hyperbole. Si je trouve donc quelque moien de la decrire aussi exactement qu'avec un compas ordinaire on decrit un cercle, n'auray je pas trouvè cette quadrature? Qu'y a-t-il plus a dire a ma construction qu'a celle d'une ligne moienne proportionelle entre deux droites donnees? Il est vray que j'ay besoin du parallelisme d'un plan a l'horizon; mais cela est possible, non pas dans la derniere justesse, mais comme la droiture d'une regle. Pour le reste je decris ma courbe presque aussi facilement qu'un cercle et la machine que j'emploie approche fort de la simplicitè du compas.
On dira que dans ma description de la courbe il peut bien plus facilement arriver de l'erreur, et beaucoup plus grande, qu'a la description d'une circonference de cercle; aussi y a-t-il plus de choses a ajuster pour decrire une Ellipse ou hyperbole, qu'il n'en faut pour le cercle’.

[p. 412]

sont entre autres la determination des points de la Catenaria, ou Chainette, & les Logarithmes.

Car quand BY est égale à AC, qu'on prend dans l'axe de la Chainette, c'est-a-dire DB égale à DC, son appliquée CG sera égale à YX¹⁶⁾. Et la même YX¹⁷⁾ est encore le Logarithme de la raison de AD à PD. C'est-à-dire, qu'elle est égale à la distance des deux lignes AD, PD, ou de quelques deux autres qui ayent la même raison, appliquées á l'Asymptote de la ligne Logarithmique, qui a DA pour tangente universelle; d'ou l'on peut trouver les Logarithmes des Tables, suivant ce que j'ay montré dans l'Addition au Discours de la cause de la Pesanteur¹⁸⁾. Mr. Leibnitz, qui a commencé le premier¹⁹⁾ à reduire la courbe de la Chainette aux loix de la Geometrie, vouloit que cette ligne formée par le moyen d'une chaine effective, & fort deliée, put servir à l'invention des Logarithmes²⁰⁾, ou

16) En effet, posant AD=a, DP=z, CG=x, CD=BD=y, on a, d'après ce qui précède, ax=aire hyp. , donc ; mais puisque , on trouve facilement , équation bien connue de la chaînette. Les manuscrits, d'ailleurs, ne donnent, cette fois encore, aucun renseignement précis sur la manière dont cette construction a été obtenue par Huygens.

17) On ajouterait aujourd'hui: divisée par AD.

18) Consultez les dernières pages de ce discours, qui traitent des propriétés de la logarithmique.

19) Voir la note 1 de la pièce N^o. 2681.

20) Voir la Lettre N^o. 2688 à la page 111 et la solution de Leibniz citée dans la note 5 de cette Lettre N^o. 2688.

[p. 413]

pour la quadrature de l'Hyperbole; quoy qu'il faille connoître pour cela, (comme il l'a bien sçu)²¹⁾ la longueur de la droite qu'il nomme le Parametre de la courbe, laquelle il n'enseigne pas comment elle se peut trouver. De sorte que nôtte quadratrice paroît preferable pour cet usage, en ce qu'apres la description son Parametre, qui est sa Tangente universelle, est donné.

Mais puis que le sujet m'a mené à la considération de la Chainette, qui a donné occasion à une des jolies recherches Geometriques de ce tems, je veux ajoûter icy une maniere assez singuliere que j'ay trouvée, pour parvenir à la construction de cette courbe; qui est ce qu'il y avoit de plus difficile dans ce qu'on s'est proposé d'en chercher.

Parmi ce que j'ay contribué pour être inseré dans les Acta de Leipsich²²⁾, avec les belles & savantes decouvertes de Messieurs Leibnits & Bernoully, j'ay dit que j'avois reduit la construction, ou l'invention des points de cette Ligne, à la quadrature d'une courbe dont l'Equation est a⁴ ∞ aaxx+yyxx; & que j'avois reconnu que cette quadrature dependoit de la connoissance de la somme des Secantes des arcs de cercle qui croissent également per minima; laquelle somme avoit été reduite il y a long-tems à la quadrature de l'Hyperbole par Jac. Gregorius dans ses Exercitations Geometriques, où il en deduit la mesure de la Ligne Loxodromique²³⁾; de quoy je ne me resouvenois pas alors.

Mrs. Leibnits & Bernoully, à ce que je puis juger, sont parvenus à cette construction par le moyen de la courbe que ce dernier represente dans la premiere Figure, qu'il donne pour resoudre ce Problême²⁴⁾; car Mr. Leibnitz m'a écrit qu'il l'avoit rencontrée aussi²⁵⁾. Et je trouve que c'est la même que celle que j'ay raportée cy-devant²⁶⁾ dont l'Equation est a⁴ ∞ xxyy-aayy; ayant sa quadrature dependante, comme j'ay dit, de celle de l'Hyperbole: quoyque je n'aye encore

21) En effet la construction des logarithmes telle qu'on la rencontre dans l'article de Leibniz, cité dans la note précédente, présuppose expressément, avec la connaissance de la chaînette ellemême, celle de son ‘parametrum’, c'est-à-dire la ligne OA de la figure de la Lettre N^o. 2688.

22) Voir la pièce N^o. 2681.

23) Voir la Lettre N^o. 2709 aux pages 185 et 186. Toutefois il ne s'agit pas chez Gregory, dans le chapitre cité dans la note 12 de cette Lettre, de la rectification de la Loxodromique, mais bien du calcul de la Longitude d'un point de cette courbe quand le point de départ, l'angle loxodromique et la Latitude sont données. Plus tard Huygens s'est aperçu de cette méprise, puisqu'on lit à la page 17 du livre I l'annotation suivante: ‘a Mr. de l'Hospital. Que je me suis abusé au Journal en disant que Greg. a donnè la dimension de la Loxodromique. C'est le Problème Loxodr.que’. Cette remarque d'ailleurs n'a jamais été transmise à de l'Hospital.

24) Voir l'article de Jean Bernoulli cité dans la note 1 de la pièce N^o. 2681. Il s'agit de la courbe LKF mentionnée dans la ‘Constructio I’ de cet article. Consultez encore la pièce N^o. 2778, qui traite de la même courbe, et surtout le dernier alinéa de cette pièce.

25) Voir la Lettre N^o. 2627 à la page 518 et le postcriptum de la Lettre N^o. 2659.

26) A la page 408 de la présente pièce.

[p. 414]

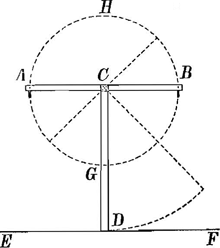
pu m'imaginer, comment le calcul les a conduits à cette ligne. Mais je passe à ma construction, qui sans considerer d'autre ligne courbe, fait trouver les points de la chainette par la dimension de la ligne Parabolique²⁷⁾.

Le premier fondement de toute recherche à l'égard de cette ligne est (Fig. III) que s'il y a une chaine composée de poids égaux, attachez à un fil comme sont BCDEF, il arrive toûjours. que de trois interstices qui se suivent, les deux lignes extrêmes, comme CD, FE, étant continuées se rencontrent dans la ligne IH perpendic. à l'horison, qui coupe l'interstice du milieu ED en deux parties égales²⁸⁾. Considerant maintenant une chaine ainsi composée de poids nouëz à égales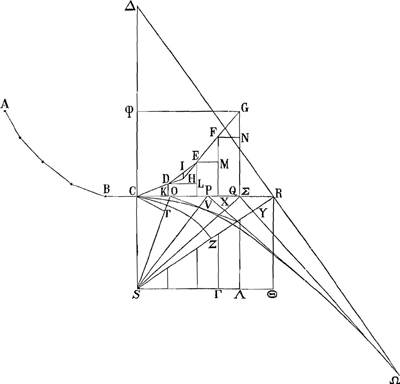

Fig. III.

distances, qu'on doit imaginer infiniment petites, & disposée en sorte que l'interstice le plus bas BC soit parallele à l'horison: si sur chacun des autres interstices,

27) Consultez, sur la première découverte de cette construction, la note 3 de la Lettre N^o. 2695.

28) Consultez, sur ce théorème, la pièce N^o. 2724, vers la fin.

[p. 415]

comme hypotenuse, on conçoit des triangles rectangles CDK, DEL &c. desquels un côté soit horisontal; on trouvera que depuis le plus bas les angles DCK, EDL, FEM &c. sont tels que leurs Tangentes croissent également comme les nombres 1, 2, 3, 4, &c. ce qui est aisé à demonstrer par le dit principe²⁹⁾, quoy que peutêtre on ne s'en seroit pas avisé sans le calcul d'Algebre.

Que si on s'imagine en suite les parties égales de la chaine CDEFG, étenduës sur la droite horisontale en COPQR, et que de la premiere division O on mene OS, qui concoure avec la perpendiculaire CS, en sorte que l'angle COS soit égal à CDO, & qu'on tire les autres droites SP, SQ, SR: les triangles SCO, SCP, SCQ, SCR, seront necessairement semblables à chacun des COD, DLE, EMF, FNG, puis que SCO est semblable à COD par la construction, & que les autres SCP, SCQ, &c. ont leur tangentes qui croissent également.

Si de plus on mene CT, OV, PX, &c. perpendiculaires sur SO, SP, SQ, &c. il est évident que les triangles CTO, OVP, PXQ &c. seront égaux & semblables aux triangles COD, DLE, EMF &c. en prenant les mêmes en ordre. D'où l'on conclud, que si les insterstices CD, DE &c. sont infiniment petits, & de même les parties CO, OP, &c. c'est-à-dire si CG est la courbe de chaine, et CR égale à sa longueur; alors la somme des TO, VP, XQ &c. sera égale à la somme des perpendiculaires KD, LE, MF &c. c'est-à-dire à la droite GΣ, ou à l'axe ϕC, (car l'interstice BC est alors compté pour rien) & que la somme des CT, OV, PX, &c. sera égale à la somme des CK, DL, EM &c. c'est-à-dire à l'appliquée Gϕ.

Or en decrivant du centre S l'arc CZ jusques sur la derniere des Secantes SR, il est aisé de voir que la somme des infiniment petites TO, VP, XQ &c. est égale à la droite retranchée ZR. Par consequent, si on suppose que CSϕ est l'axe de la chaine, & la ligne CS de certaine longueur, & que l'on prenne Cϕ égale à ZR, excés de quelque secante SR sur le rayon SC; & l'appliquée ϕG égale à la somme de toutes les CT, OV, PX &c. jusques à celle qui tombe sur SR; le point G sera dans la courbe de la chaine, dont la longueur CG sera égale à la droite CR. Mais il est question de trouver cette somme des infinies CT, OV, PX &c. laquelle j'obtiens par cette consideration, que les angles SOV, SPX, SQY peuvent être censez droits, comme en approchant infiniment pres; & qu'alors les lignes OV, PX &c. étant prolongées des deux côtez, comme aussi RΩ perpendiculaire sur SR, elles deviennent les tangentes de la Parabole CΩ, dont le sommet est C, l'axe CS, le foyer S, faisant SC un quart du Parametre; & que chacune est coupée en deux également par la droite CR; l'une moitié étant jusqu'a l'axe, l'autre jusqu'au point d'attouchement, comme ΩΔ est coupée en R: ce qui se demontre facilement. D'icy j'apprens en suite, par l'Evolution des lignes courbes, dont j'ay

29) Voir le § I de la pièce N^o. 2625.

[p. 416]

traité au livre de Horologio Oscillatorio³⁰⁾, que la somme de toutes les QY, PX, OV, CT, doit être égale à l'excés de la courbe parabolique ΩC sur la droite ΩR.

Ce que les Geometres compendront assez facilement³¹⁾, sans que je m'arrête à le prouver plus au long; n'ayant pas dessein d'écrire icy des demonstrations, mais d'indiquer seulement les voyes de l'invention.

Etant donc donné le Parametre SC de la chainette, si on prend dans l'axe quelque point Φ, & qu'on decrive du centre S avec le demidiametre Sϕ un arc de cercle qui coupe CR, tangente au sommet, en R; la tangente RΩ menée à la dite parabole du point R, étant ôtée de la longueur de sa courbe CΩ, qu'on suppose pouvoir être mesurée, le reste sera pour la droite à appliquer, ϕG; et ainsi par la même Parabole on trouvera tant de points qu'on veut dans cette courbe. J'ay envoyé cette construction à Mr. Leibnits des le commencement de Sept. en 1691³²⁾.

On peut au reste remarquer en passant, que la courbe CG, (en prenant toûjours le nombre des interstices infini, & par là le point C comme dans l'axe, & pour sommet) sera égale à la droite CR³³⁾. Et que la dimension de l'espace de la courbe se demontre encore d'icy sans peine, en achevant le rectangle RCSΘ, & en prolongeant les perpend. GN, FM &c. jusques sur SΘ, en Λ, Γ &c. parce qu'il paroit que le triangle SQY est la moitié du rectangle FΛ, ayant la base & la hauteur de même. Et pareillement le triangle SPX la moitié du rectangle EΓ. & ainsi les autres en suite. Et par consequent le triangle SCR égal à la moitié de l'espace SCGΛ³⁴⁾. Je pourrois montrer de même, en abregé, les fondemens de tout ce qui a été trouvé touchant cette Ligne courbe. Mais j'estime que cela appartient plûtôt à Messieurs Leibnits & Bernoulli, qui y ont plus de part que moy; & il faut les prier pour l'utilité du public de vouloir prendre cette peine.

J'aurois fini icy, sans une lettre que je viens de recevoir de Monsr. le Marquis de l'Hospital³⁵⁾; ou ayant trouvé deux choses remarquables en ces matieres, je ne puis m'empêcher d'en dire quelque mot. L'une est la construction, avec plusieurs proprietez de la Ligne Courbe de Mr. de Beaune, que Mr. Descartes dans sa lettre 79 du 3 vol. dit luy avoir été proposée à trouver par la proprieté donnée

30) Voir la ‘Pars Tertia: De linearum curvarum evolutione et dimensione’.

31) C'est-à-dire en se représentant comme tracées les développantes successives passant par les points C, O, P, etc. La même méthode fut employée par Huygens dans la pièce N^o. 2671.

32) Voir la Lettre N^o. 2695.

33) C'est la rectification indiquée par Leibniz dans sa Lettre N^o. 2688 à la page 111 et dans sa solution du problème de la chaînette, citée dans la note 1 de la pièce N^o. 2681. Huygens la retrouva dans le § I de la pièce N^o. 2694, où il démontre, d'une manière moins directe que dans la pièce présente, l'égalité des lignes RS et Sφ de la présente figure. Elle diffère de celle que Huygens avait annoncée dans la pièce N^o. 2681 et démontrée au § III de la pièce N^o. 2625.

34) Comparez le § I de la pièce N^o. 2694.

35) La Lettre N^o. 2787.

[p. 417]

de sa Tangente: Probleme qui m'a paru très-difficile. On en trouvera la solution de Mr. le Marquis dans le 34. Journal des Sçavans de l'année derniere³⁶⁾; c'est pourquoy je ne la raporte point.

L'autre est sa reponse touchant une autre Courbe fort connuë, & que Mr. Descartes a encore considerée autrefois, comme aussi Mr. Hudde³⁷⁾, du tems que ses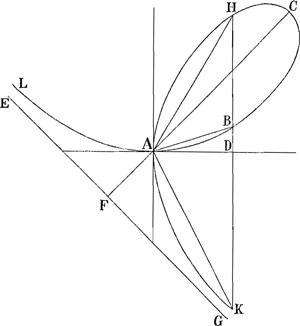

Fig. IV.

emplois dans la Repub. ne l'empêchoient pas de vaquer à ces études. C'est celle dont vous voyez icy la Figure, (Fig. IV) enfermant la feuille ABCH, & continuant son trait de part & d'autre le long de l'Asymptote EFG. Son équation est x³+y³ ∞ xyn, quand AD est x prise dans la droite qui fait un angle de 45. degr. avec le diametre CA; la perpendiculaire DB, ou DH, ou DK, y, & n une ligne droite donnée. Luy ayant mandé³⁸⁾ que j'avois trouvé la quadrature de cette Courbe, & que le contenu de la feuille ABCH était egal à ⅙ nn, c'est-a-dire à un tiers du quarré du diametre AC; que l'espace infini entre l'Asymptote et les deux continuations etoit encore de même grandeur; & que la quadrature generale des segments s'exprimoit par un seul terme; il n'a pas manqué de trouver au vray cette quadrature generale. Savoir que le contenu des segments AH, ou AK, s'exprime par nxx/6y, & du segment AB par nyy/6x. Mais de plus il m'assûre d'y être parvenu par trois voyes differentes. Ce que j'admire, croyant avoir fait quelque chose d'en avoir trouve une. Je suis, &c.

36) Voir l'article cité dans la note 2 de la Lettre N^o. 2787.

37) Voir les notes 21 et 22 de la Lettre N^o. 2777.

38) Dans la Lettre N^o. 2777.