Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2787.
| |
[pagina 391]
| |
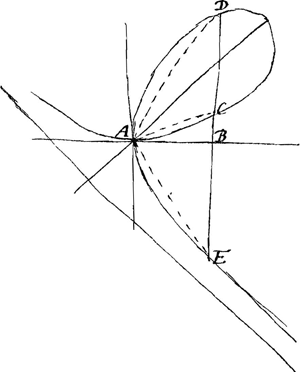
que a∛4/3 sauoir deux urayes BC, BD, et vne fausse BE egale aux deux vrayes; que les deux racines urayes deuiennent egales entr'elles lorsque x=a∛4/3 et qu'enfin elles deuiennent imaginaires, et que la fausse seule demeure réelle lorsque x surpasse a∛4/3 La quadrature generale que vous me marquez s'exprimer par vn terme est celle-ci, le segment AD ou AE=axx/6y (AB=x, BD ou BE=y) et le segment AC=ayy/6x(BC=y). J'y suis paruenu par trois differentes manieres, et ie serois bien aise que vous me proposassiez quelques courbes dont vôtre methode donne la quadrature pour essayer si les miennes sont aussi generales que la vôtre. Je vous enuoye la solution du probleme que Mr. de Beaune proposa autre fois à Mr. Descartes, et qu'on trouue dans la 79e de ses lettres tome 3, telle que ie l'ai faite inserer dans le 34e journal de l'année derniereGa naar voetnoot2). | |
Probleme.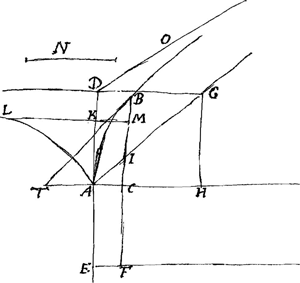 Vne ligne droite quelconque N etant donnée, et ayant mené deux autres lignes indefinies AC, AI, en sorte que l'angle CAI soit de 45 degrez; on demande la maniere de décrire la courbe ABB qui soit de telle nature, que, si l'on mene d'vn de ses points quelconques B, l'ordonnée BC, et la touchante BT, la raison de BC à CT soit toujours la mesme que celle de la droite donnée N à BI. Ayant formé le quarré AG qui a pour côté la droite | |
[pagina 392]
| |
AH egale à la ligne donnée N, on décrira entre les asymptotes GD, GH, par le point A l'hiperbole ALL, et ayant prolongé DA en E, en sorte que AE soit egale à AH, on prendra le rectangle EC egal à l'espace hiperbolique AKL, on prolongera les droites LK, FC, jusqu'à ce qu'elles se rencontrent en vn point M, et on prendra enfin IB egale à CM, je dis que le point B sera à la courbe qu'il falloit décrireGa naar einda). Il est euident que la nature de cette ligne courbe ABB depend de la quadrature de l'hiperbole, et qu'ainsi elle est mecanique dans le sens de Descartes. Voici maintenant quelques vnes de ses proprietez. 1o. Elle a pour asymptote la ligne DO parallele à AI. 2o. Si l'on nomme AC, x, BC, y, l'espace ABC compris par les droites AC, CB et par la portion AB de la courbe=xy-½yy+nxGa naar voetnoot3). 3o. La distance du centre de grauité de l'espace ABC de la droite AC=n++3xyy-2y3/6xy-3yy+6nx et de AK=½n+3xxy-y3/6xy-3yy+6nxGa naar voetnoot4), et on a par consequent les solides, demi-solides &c. formez par la reuolution de cet espace, tant autour de AC que de AK ou BC. 4o. Jl est facile de determiner les centres de grauité de ces demi-solides. Mais comme on a besoin d'vne adresse particuliere pour rectifier cette courbe; en supposant la quadrature de l'hiperbole, je propose ce probleme aux geometres, les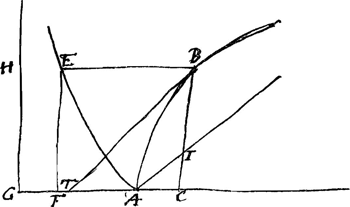 | |
[pagina 393]
| |
assurant qu'il merite leur rechercheGa naar voetnoot5). Je vous envoirai, si vous souhaitez, le chemin que j'ai tenu pour arriuer à cette construction. Mais j'en ai trouue depuis vne autre qui me plait davantage et dont vous iugerez. Ayant pris sur CA prolongée du côté de A, la partie AG egale à la droite donnée N, et mené GH parallele à BC, on decrira par le point A la logarithmique AE, qui ait pour asymptote la droite indefinie GH, et pour soutangente vne ligne egale à AG. On menera ensuite par vn point quelconque E de la logarithmique les droites EF, EB paralleles à GH, GA, et ayant pris EB egale à EF, je dis que le point B sera à la courbe requise. Jl est facile de rendre cette construction generale quelque puisse estre l'angle donné CAI. Pour ce qui est de la courbe qui a pour soutangente √ay+xx j'etois dans la pensée lorsque ie vous ecriuis la derniere fois qu'elle tomboit dans ma regle, mais ayant voulu acheuer le calcul pour vous l'enuoyer j'ai trouué que ie me trompois, je ne desespere pas cependant d'en uenir a bout car cette regle se perfectionne tous les jours, je puis trouuer par son moyen les courbes qui ont pour soutangente a3y+axxy/axy+aax+x3 et yy+xy/y, dont je vous feray part si vous souhaités. Je ne connois point la regle des tangentes de Mr. de Roberual dont vous me parlez, est elle differente de celle de Mrs. Barrou et LeibnitsGa naar voetnoot6). J'ay vne grande impatience de voir la methode de Mr. Neuton pour l'inverse des tangentes, et comme je ne doute pas que vous n'en ayez bien tost des exemplaires en holande, je vous aurois la derniere obligation si vous uouliez bien m'en enuoyer vn par la poste, et au cas qu'elle soit iointe au liure de Vallis de Algebra il faudroit l'en separer, et pour le reste du liure je vous manderois a qui il le faudroit donner pour me le faire tenir, je vous demande mille pardons de la liberté que ie prends, mais ce n'est qu'à deux conditions l'vne que vous me mandiez l'argent que le liure vous aura coûté afin que ie vous le fasse rendre comme cela est dans l'ordre, et l'autre que vous uouliez bien vous seruir de moi lorsque vous aurez quelque commissions à donner pour ce payis. Je suis de vostre auis que la geometrie n'est qu'vn ieu d'esprit si on ne l'applique à la phisique et aux inuentions de mecaniques, mais il est rare, qu'on y reussisse et il faut des siecles entiers pour produire vn Hugens. La prettenduë inuention de Mr. Hautefeüille est tombée et les orlogeurs, auec lesquels il s'etoit accommodé disent qu'elle ne peut pas reussir. J'ai | |
[pagina 394]
| |
vû il y a enuiron deux ans à la foire St. Germain vn homme qui montroit vne teste d'airain qui contrefaisoit Democrite et qui prononçoit quelques mots mais si c'est celle dont vous me parlez vous n'auez guere perdu à ne la point uoir car ayant approfondi la chose je reconnus que ce n'etoit qu'vne tromperie et que c'etoit vn homme qui etoit caché et qui parloit au trauers de quelques tuyaux qui conduisoient la uoix à la teste, et mesme l'artifice étoit grossier. J'ai uû il y a quelques jours Mr. le Duc de RoanezGa naar voetnoot7), à qui j'ai fait vos complimens, ilm'a paru fort surpris de ce que vous n'auiez point eu de ses nouuelles et il m'a assuré, qu'il auoit prié Mr. de la Hire et quelques autres, qu'il croioit auoir commerce de lettre auec vous de vous marquer sa reconnoissance de ce que vous lui auiez enuoyé vôtre traitté de la lumiere qu'il m'a dit trouuer parfaitement beau. Jl est fort aise d'auoir trouué vne voye sure pour renoüer commerce, et pour vous en donner des marques voici vn papier qu'il enuoye qui contient les auantages d'vne nouuelle inuention d'vne porte d'ecluse et il me semble qu'il souhaite que vous mettiez au bas de ce memoire en le renuoyant que supposé que ce qu'il contient soit urai vous trouuez l'inuention nouvelle, &c. Il uous enuoira aussi tost que nous aurons vôtre reponce, le modelle de cette porte et la maniere dont on la fait. Je suis auec beaucoup d'estime
Monsieur Vostre treshumble et tresobeissant seruiteur Le Marquis de lHospital.
A Paris le 12e feurier 1693. |
|