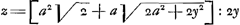Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2765.
| |
[pagina 313]
| |
pression, data qualibet linea &c.Ga naar voetnoot4) Je vous en feray part si vous jugez que cela en valle la peine, j'espere que vous voudrez bien m'enuoyer les problemes qui regardent les tangentes et les quadratures afin de pouuoir m'exercer à les resoudre. Si vous y vouliez joindre quelques problemes fisicomathematiques comme je vois que ce sont ceux-la qui vous plaisent dauantage je m'y appliquerois avec soin. Je suis Monsieur avec vne estime tres singuliere
Monsieur
Vostre tres humble et tres obeissant seruiteur le M de l'Hospital.
A Ouques, ce 10e Septembre 1692. | |
[pagina 314]
| |
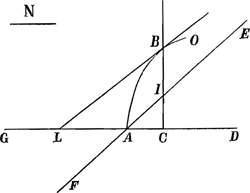
Theor.Soit la courbe logarithmique indefinie ABCD, qui a pour asymptote la droite TE, d'un point quelquonque E de cet asymptote ayant mené la perpendiculaire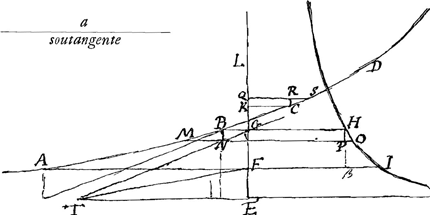 EL, soit décritte la courbe geometrique HI, dont la nature soit exprimée par cette equation (EF ou EG ∞ y, FI ou GH ∞ z), 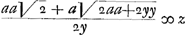 . ou en ostant les jncommensurables, aay+2aaz√2 ∞ 2yzz. que l'on mene à present deux paralleles quelconques AFI, BGH, à l'asymptote TE, et ayant pris TE ∞ a, EL ∞ FI, EK ∞ GH, et mené les droites TG, TF, et les paralleles LD, KC, qui rencontrent la logarithmique aux points D, C; je dis que la portion AB de cette logarithmique ∞ TG-TF+LD-KC. . ou en ostant les jncommensurables, aay+2aaz√2 ∞ 2yzz. que l'on mene à present deux paralleles quelconques AFI, BGH, à l'asymptote TE, et ayant pris TE ∞ a, EL ∞ FI, EK ∞ GH, et mené les droites TG, TF, et les paralleles LD, KC, qui rencontrent la logarithmique aux points D, C; je dis que la portion AB de cette logarithmique ∞ TG-TF+LD-KC.
| |
Demonstration.Ayant pris l'arc BM jnfiniment petit, et mené MO parallele a BH, l'on nommera comme fait Mr. Leibnitz, BN, ou HP, dy, MN dx, et l'on aura par la proprieté de la logarithmiqueGa naar voetnoot5),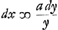 , d'ou l'on tire BM ou , d'ou l'on tire BM ou 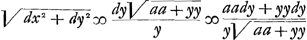 . Or jl est clair que la somme des . Or jl est clair que la somme des 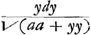 , ,
| |
[pagina 315]
| |
dans la portion AB, ∞ TG-TE, de sorte qu'il ne reste plus qu'à demontrer que la somme des 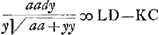 , ce que je prouue ainsi. Soit prise KQ ∞ OP, et soit menée QS. l'on trouuera par la methode des tangentes de Barrow ou de Mr. Leibnitz, que OP ou , ce que je prouue ainsi. Soit prise KQ ∞ OP, et soit menée QS. l'on trouuera par la methode des tangentes de Barrow ou de Mr. Leibnitz, que OP ou 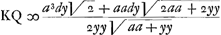 Ga naar voetnoot6). Or par la proprieté de la logarithmique Ga naar voetnoot6). Or par la proprieté de la logarithmique 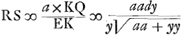 ; donc la somme des RS, c'est-à-dire LD-KC ∞ à la somme des ; donc la somme des RS, c'est-à-dire LD-KC ∞ à la somme des 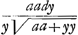 dans la portion AB, donc &c. dans la portion AB, donc &c. |
|


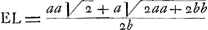 mais comme il me paroist que vous faittes quelque cas de cette inuention je vous enuoye le mesme theoreme enoncé vn peu autrement auec vne demonstration fort courte mais qui suffira, a ce que je pense, pour vous conuaincre de sa verité. Les deux manieres dont vous vous estes pris pour reduire tout d'vn coup la construction de la ligne d'vne chaine pendante à la quadrature de l'hyperbole sans auoir besoin de passer par l'une ou l'autre de ces courbes, xxyy=a4-aayy ou xxyy=4a4-x4
mais comme il me paroist que vous faittes quelque cas de cette inuention je vous enuoye le mesme theoreme enoncé vn peu autrement auec vne demonstration fort courte mais qui suffira, a ce que je pense, pour vous conuaincre de sa verité. Les deux manieres dont vous vous estes pris pour reduire tout d'vn coup la construction de la ligne d'vne chaine pendante à la quadrature de l'hyperbole sans auoir besoin de passer par l'une ou l'autre de ces courbes, xxyy=a4-aayy ou xxyy=4a4-x4