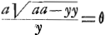Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 418]
| ||||||||||||||||
No 2794.
| ||||||||||||||||
§ IGa naar voetnoot2).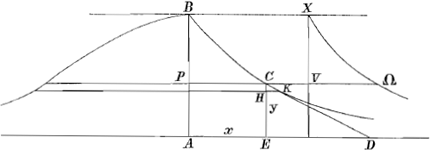 Fig. I.
Quadratura Hyperbolae per novam quadraticem ejus, quae uno ductu describitur. BA, AD normales; tangens CD semper aequalis AB.
mutari ante in a, omissa multiplicatione per a.
dimensionem ad quadraturam hyperbolae reduxi in lib. GGa naar voetnoot3). | ||||||||||||||||
[pagina 419]
| ||||||||||||||||
§ IIGa naar voetnoot4).
sed ϰ sunt aequalia ut et a. Ergo  aa/a-x (spat. hyperb. BXΩP): aa/a-x (spat. hyperb. BXΩP): a(▭ VB)= a(▭ VB)= aϰ/a-x: aϰ/a-x: ϰ, hoc est ut curva CB ad BP rectam. ϰ, hoc est ut curva CB ad BP rectam.
Ergo si curva BC ponatur data, poterit ejus opera inveniri partium ejus longitudo rectae lineae aequalisGa naar voetnoot5). | ||||||||||||||||
[pagina 420]
| ||||||||||||||||
§ IIIGa naar voetnoot6).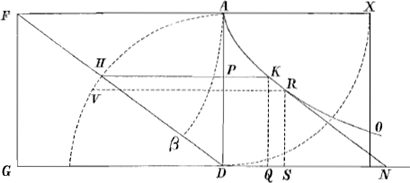 Fig. 2.
ad experiendam veritatem curvae per logarithmos, sumatur quaelibet DP. sit PH parall. DG, secans arcum quadr.is in H. ducatur recta DHF. fiat Fβ=FA. quaeratur logarithmus rationis AD ad Dβ, hoc est diff.a logar.orum AD et Dβ in tabulis; et ut 43420 ad dictam diff.m ita sit AD ad aliam, cui aequalis sumatur HK ea debebit incidere in punctum curvae. | ||||||||||||||||
§ IVGa naar voetnoot7).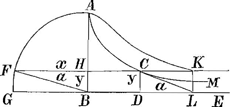 Fig. 3.
AC Tractoria. asympt. BE. CL tangens. CK=DL. HF=CK.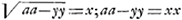 . .
F est in circumferentia circ. Spat. HFGB=spat.o infinito DCMEGa naar voetnoot8). | ||||||||||||||||
[pagina 421]
| ||||||||||||||||
§ VGa naar voetnoot9).Solidum ex conversione ejus spatij circum asymptoton erit aequale sphaerae quartae parti, cujus AD [voir la fig. 2] semidiameter. hinc et centri gravitatis distantia ejusdem spatij ab asymptoto habebitur, pendens a circuli quadratura. triangula quadrantis ADX circa AX revoluta considerantur quibus respondent singula Δla in spatio curvae et asymptoti conversa circa hanc ipsamGa naar voetnoot10). | ||||||||||||||||
§ VIGa naar voetnoot11).Superficies istius solidi infiniti, praeter basin, aequatur circulo cujus semidiameter duplum potest lateris AD [voir la fig. 2]. Suntque superficies ex portionibus circa asymptoton sicut abscissae ipsis respondentes ad verticem AGa naar voetnoot12). Quia igitur portionum longitudo invenitur ipsius curvae opera Ergo et centra gravitatis ipsarum respectu asymptoti, et hinc superficies portionum ex conversione circa AX ad circulos redigentur. | ||||||||||||||||
[pagina 422]
| ||||||||||||||||
§ VIIGa naar voetnoot13).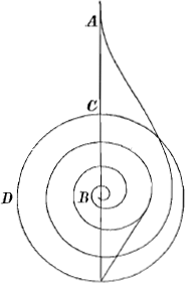 Fig. 4.
Talis quaepiam infinita spiralis describeretur si pes ductor per circuli circumferentiam iret, sequente cuspide ab A puncto; ductore in C. Et similis alia ducendo versus DGa naar voetnoot14). |
|


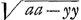 ; ϰy/λ=
; ϰy/λ=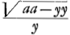 , rejice ϰ et λ. Vel poterant
, rejice ϰ et λ. Vel poterant