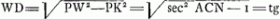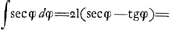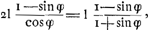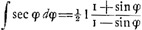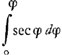Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 182]

N^o 2709.
Christiaan Huygens à G.W. Leibniz.
16 novembre 1691.

La lettre se trouve à Hannover, Bibliothèque royale.
La minute se trouve à Leiden, coll. Huygens.
La minute a été publiée par P.J. Uylenbroek¹⁾, la lettre par C.I. Gerhardt²⁾.
La lettre est la réponse au No. 2699.
Leibniz y répondit le 8 janvier 1692.

A la Haye, ce 16 Novembre 1691.

Monsieur

Je me suis ces deux derniers mois abstenu de l'etude et du travail, ayant de la peine à conserver ma santé dans un temps ou une infinitè de monde dans ce pais est tombée malade. C'est ce qui est cause que je respons si tard à voste derniere lettre du 11/21 Sept. Je m'en vais maintenant le faire par ordre pour ne rien oublier; mais auparavant je vous remercieray d'avoir reparè l'erreur de Mrs. de Leipsich, touchant ma Progression dans l'Hyperbole³⁾, et surtout de l'honneur que vous m'avez fait dans les Acta de Sept. dernier en publiant que mes escrits autrefois vous ont estè de quelque utilitè⁴⁾.

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 103. La rédaction de la minute ne diffère pas notablement de celle de la lettre.

2) Leibnizens Mathematische Schriften, Band II, p. 109 et Briefwechsel, p. 670.

3) Voir la note 14 de la Lettre N^o. 2636.

4) Il s'agit du passage remarquable que, dans la note 12 de la Lettre N^o. 1919, nous avons extrait de l'article de Leibniz intitulé:
G.G.L. De solutionibus problematis Catenarii vel Funicularis in Actis Junii A. 1691 aliisque a Dn. I.B. propositis.
Pour compléter les diverses pièces et lettres qui se rapportent à la solution que Huygens a donnée du problème de la chaînette, nous faisons suivre encore de cet article les lignes, dans lesquelles Leibniz fait la comparaison des trois solutions, publiées dans les Acta de juin 1691. ‘Valde delectatus sum lectis tribus Problematis a Galilaeo propositi a D. Bernoullio renovati, solutionibus inter se consentientibus, quod indicium est veritatis, apud eos valiturum, qui talia accurate non examinant. Etsi autem omnia conferre non vacaverit, in summa tamen rei manifesta est concordia. Legem tangentium, & extensionem curvae catenariae in rectam invenimus omnes, & cum curvedinis mensuram olim in Actis Junii A. 1686, p. 489 (introducto novo contactus genere, quem osculum appellare placuit) explicuerim per radium circuli curvam osculantis, seu ex omnibus circulis tangentibus maxime ad curvam accedentis, eundemque adeo quem ipsa curva ad rectam facientis angulum contactus, placuit celeberrimo Hugenio (animadvertenti centra horum circulorum semper incidere in lineas a se primum inventas, quarum evolutione describuntur datae) speculationem huc applicare, & investigare radium curvitatis vel circulum osculatorem curvae catenariae, sive ejus curvam evolutione generantem, quam & dedit solutio Bernoulliana. In Hugeniana autem, distantia quoque habetur centri gravitatis catenariae ab axe. In Bernoulliana & mea, ejusdem distantia tam ab axe quem & a basi aut alia recta, adeoque puncti determinatio, item quadratura figurae catenariae. Quibus ego in mea centrum gravitatis etiam hujus figurae seu areae adjeci. Constructionem lineae Dn. Hugenius exhibet ex supposita quadratura curvae, qualis est xxyy=a⁴-aayy, Dn. Joh. Bernoullius & ego reduximus ad quadraturam hyperbolae; illo perbene adhibente extensionem curvae parabolicae in rectam, me denique rem omnem reducente ad logarithmos, eaque ratione obtinente, perfectissimum in Transcendentibus exprimendi pariter & construendi genus. Sic enim unica tantum semel supposita vel habita ratione constante, de reliquo infinita puncta vera exhiberi possunt per communem Geometriam sine interventu ulteriore quadraturarum aut extensionum in rectas. Lineae Catenariae mirum & elegantem cum Logarithmis consensum, ex mea constructione animadvertere fortasse non injucundum videbitur. Caeterum a Dn. Hugenio (egregii ex Tab. Sinuum compendii nobis spem faciente) observatum est, rem eam reduci ad summam secantium arcuum, per minima aequaliter crescentium.

[p. 183]

Vous me parlez à propos de la courbure de la chainette, de vostre discours de angulo Contactus et Osculi^a). Vous pouvez bien croire qu'en ce lisant je ne trouvay pas cette considération nouvelle, parce que ces sortes de contact entrent naturellement dans mes Evolutions des Lignes courbes⁵⁾.

Je me souviens aussi que longtemps devant que de publier ce Traité j'avois communiquè à van Schoten quelque remarque là dessus⁶⁾, scavoir de la circon-

a) Juni 86 [Christiaan Huygens].

5) Il s'agit de l'Horologium Oscillatorium, Pars tertia: De linearum curvarum evolutione et dimensione.

6)




On rencontre cette remarque dans la pièce N^o. 204, d'octobre 1654, au bas de la page 305. Van Schooten en a fait usage dans la seconde édition (de 1659) de l'ouvrage cité dans la note 1 de la Lettre N^o. 150, en insérant à la page 339 le passage suivant: ‘Praeterea hinc constat, (quod sane animadversione dignum) si recta tangens Parabolam in aliquo puncto extra verticem ipsa ibidem quoque tangatur a Circulo non per verticem transeunte, quique Parabolam in eodem puncto secet, hoc est, ut rectae NM, CB, et DE omnes tres sint inter se aequales: quòd tunc quidem HI ipsius NM, CB, vel DE tripla sit futura’.

[p. 184]

ference, qui coupant une parabole, semble la toucher au mesme point, c'est à dire que dans la parabole comme aussi dans les autres sections coniques il n'y a que le point du sommet où une circonference la puisse baiser; cela arrive encore en plusieurs cas d'autres lignes courbes, quoy qu'il me semble que vous n'en avez rien dit⁷⁾.

Puisque j'ay bien jugè en quoy doit consister l'avantage que donne vostre nouveau calcul, je souhaiterois fort de voir comment il vous a fait trouver directement et sans essort d'imagination l'ἀπαγωγὴ de la Construction de la Chainette à la quadrature de l'Hyperbole ou aux Logarithmes. En effet vous devez donner au public cet exemple de vostre methode, a fin qu'on voie de plus en plus son utilitè et que les Geometres puissent profiter de nostre exercitation. Pour moy si je trouve en suite que j'aye quelque chose de different dans mes recherches et qui merite d'estre sceu, je le publieray aussi tres volontiers⁸⁾. Cela sera peu, mais il y aura pourtant une maniere fort belle pour parvenir à la construction de la Courbe⁹⁾ et que je scay estre differente de la vostre par les choses que vous me mandez, comme aussi différente de celle de Mr. Bernoully, par ce que je conjecture de son escrit inserè aux Acta.

Pour ce qui est du doute que j'avois proposè, je me tiens plus que satisfait apres avoir vu vostre exacte justification. Il est vray que quand j'ay lu ces mots de querelle et d'avoir perverti le sens des paroles de Mr. Bernoulli, j'ay dit bona verba, car en effet j'y estois allè de bonne foy, et le soupçon qui m'estoit restè estoit de trop peu d'importance pour que vous usassiez de tels termes en le resutant. Quand je vous en parlay, c'estoit que j'aurois estè bien aise de trouver que vous eussiez estè aussi peu clairvoiant que moy, dans cette question. Socium tarditatis meae quaerebam. Ce que vous me dites de n'avoir rien pu tirer de France ni d'Italie sur ce probleme, peut servir à me consoler, et marque qu'il n'est pas des plus faciles.

Ce n'est pas le jeune Bernoulli, mais l'ainè qui a travaillè sur la ligne Loxodromique, et j'ay trouvè etrange, qu'apres que vous eussiez donnè la bonne Con-

7) La minute ajoute encore la phrase suivante: La quadrature de la courbe de la génératrice de la chaînette pourrait avoir de la difficultè si on proposait de la trouver; mais j'en sais peu de cas, parce que cette courbe paroit inutile ‘et longe posita’.

8) Voir l'article de Huygens, cité dans la note 2 de la pièce N^o. 2694.

9) Il s'agit de la construction indiquée dans la Lettre N^o. 2695.

[p. 185]

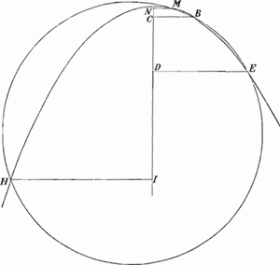
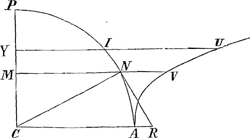
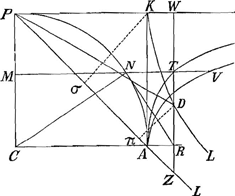
struction pour trouver la longitude par la quadrature de l'Hyperbole, il se soit avisè trois mois apres, d'en donner une qui demande la dimension d'un espace inconnu et qui comprend une étendue infinie¹⁰⁾, cela s'appelle expliquer ignotum per ignotius.

J'ay regardè dans le Tiphys Batavus de Snellius, depuis que vous m'en avez averti, comment il demontre par des propositions aisées, que cette invention des Longitudes, scavoir quand la Latitude et l'angle Loxodromique est donnè, depend de la somme des secantes. Il n'est pas allè plus loin; mais scaviez vous, Monsieur, que Jac. Gregorius dans ses Exercitations Geometriques a reduit cette somme à l'espace qui chez vous est VMCA¹¹⁾, et qu'il a egalè cet espace à un espace hyperbolique?¹²⁾ Je crois certainement que vous ne vous en estes point souvenu, non plus que moy; car j'aurois pu par là achever de trouver la con-

10) En effet, dans l'article cité dans la note 32 de la Lettre N^o. 2693, Jacques Bernoulli fait dépendre la construction de la loxodromique, partant d'un point donné de l'équateur sous un angle donné, de la quadrature d'une aire comprise entre une courbe et son asymptote.

11) Voir la figure de la note 9 de la Lettre N^o. 2699.

12) Le passage en question se trouve dans le livre cité dans la note 2 de la Lettre N^o. 1684 au chapitre intitulé: ‘Analogia inter Lineam Meridianam Planispherii Nautici et Tangentes Artificiales Geometricè demonstrata; seu, quod Secantium Naturalium additio efficiat Tangentes Artificiales’.
Pour montrer jusqu'à quel point James Gregory avait en effet devancé, dans son livre de 1668 qui est devenu très rare, les résultats obtenus par Leibniz que nous avons mentionnés dans la note 9 de la Lettre N^o. 2699, nous reproduisons ici, en laissant de côté les démonstrations assez compliquées, les Propositions I et II ainsi que le premier ‘Consectarium’ du chapitre cité, tout en changeant les lettres des figures de Gregory pour les rendre conformes avec celles de la figure de Leibniz.




Prop. I. Theorema. Sit Circuli quadrans CAP, cujus pars sit arcus AI; super arcu AI imaginetur portio superficieï Cylindrici recti talis naturae, ut (sumpto in arcu AI quodlibet puncto N) perpendicularis ad planum CPA ex puncto N ad summitatem portionis superficiei cylindricae excitata semper fiat aequalis secanti arcus NA. Deinde sit mixtilineum UIYCA talis naturae ut (ducta in eo recta MV radio AC parallela et arcum quadrantis secante in puncto ad libitum N) recta VM, secans [CR] arcus NA, et radius CA sint continuè proportionales. Dico mixtilineum UYCA esse aequale dictae portioni superficiei cylindricae.




Prop. II. Sit circuli quadrans CPA, sitque mixtilineum STACPS talis naturae, ut (ducta recta ad libitum TM radio AC parallela et quadranti arcum secante in N) recta TM aequalis sit secanti [CR] arcus AN, sitque mixtilineum SVACPS talis naturae ut (productâ arbitrariâ MT in V) rectae CA, MT, MV sint continuè proportionales: deinde sit Semihyperbola KDL cujus axis PS, vertex K et asymptoton PAL: ducatur ad libitum radio CA parallela recta MV, curvas ANP, ATS, AVS secans in punctis N, T, V, et per punctum T ducatur radio PC recta parallela TR Hyperbolae occurrens in puncto D. Dico Sectorem Hyperbolicum KPD aequalem esse semissi Figurae VACM, quae Figura (ut in antecedente demonstratum est) aequalis est superficiei cylindricae conflatae ex omnibus secantibus arcuum infinitorum NA plano APC in debitis suis punctis N normaliter insistentibus.
Consectarium. Hinc sequitur, quod Figura VACM semper sit dupla Logarithmi differentiae inter tangentem et secantem arcus NA, posito radio AK loco unitatis, quod sic probo. Ex punctis K, D in asymptoton PL demittantur perpendiculares Kσ et Dπ; ex demonstratis in Circ. et Hyperb. Quad. manifestum est sectorem PKD esse aequalem Figurae KDπσ, item Figuram KDπσ esse Logarithmum rectae Dπ positâ Kσ unitate; ut autem Kσ ad Dπ ita PK radius ad DZ differentiam inter tangentem [DW] et secantem [ZW=PW=CR] et ideo posita KA unitate erit idem sector PKD Logarithmus rectae DZ, nempe excessus qua secans arcus NA superat ejusdem tangentem’.
Comme on le voit, la première proposition réduit le calcul de l'intégrale ∊secφ dφ à la quadrature de l'aire MVAC, qui, par construction, est identique avec l'aire homonyme de la figure de la note 9 de la Lettre N^o. 2699.
Dans la seconde proposition cette aire est remplacée par une aire hyperbolique, qui se calcule facilement de la manière indiquée dans le Consectarium, parce que PW=CR=sec ACN par construction, et ACN, par suite de l'équation analytique de l'hyperbole équilatère KDL.
D'après ce ‘Consectarium’, on aurait la relation , qui ne diffère de la vraie relation que par le signe et par le facteur 2, qui s'y est glissé par mégarde, puisque Gregory a oublié que le carré décrit sur l'axe de l'hyperbole PK comme diagonale est égal à ½ et non pas à l'unité et qu'on doit donc égaler l'aire de la figure hyperbolique KDπσ à la moitié du l Dπ/Kσ.

[p. 186]

struction de la Chainette¹³⁾, et plus facilement que par vostre calcul sur la Loxodromique, que je n'entendois pas, et que je n'ay demeslè que longtemps apres. Il

13) On rencontre cet achèvement, sous la date du 1^er octobre, à la page 127 verso du livre G. En se servant des recherches de Gregory, Huygens y démontre que l'aire δαψχ de la figure 5 de la pièce N^o. 2625, dont il avait fait dépendre la construction par points de la chaînette et dont il avait réduit la quadrature à la sommation des sécantes au § I du N^o. 2634, égale le double de l'aire hyperbolique KσπD de la figure 2 de la note précédente, lorsque l'on suppose que l'arc AN est identique avec l'arc αII de la figure 5 du N^o. 2625.

[p. 187]

paroit par un passage dans les notes de Albert Girard sur Stevin, qu'il doit avoir sçu la solution de cette mesme question des Longitudes. Car il parle de la difference entre la methode de Snellius par la Table des sommes des secantes et la methode parfaite, qu'il dit estre beaucoup plus courte; et il propose la dessus ce probleme, dont il promet la solution: scavoir quand l'angle loxodromique est donné de 89 degrés, combien de tours entiers et de degrez de longitude par dessus fera un vaisseau, en partant d'un point sous l'Equateur pour arriver à la latitude de 89 degrez, et combien le point où il entrera dans ce parallele sera distant alors du lieu de son depart, le tout sans Tables¹⁴⁾. Je l'ay calculè par plaisir et j'y trouve 43 tours, 85 deg. 57 min.¹⁵⁾. On ne connoissoit pas encore en ce temps

14) Il s'agit d'une note d'Albert Girard, qui se trouve à la page 168 du second volume de l'ouvrage suivant qui parut deux ans après la mort de Girard: ‘Les OEuvres Mathématiques de Simon Stevin de Bruges. Ou sont inserées les memoires mathematiques, Esquelles s'est exercé le Tres-haut & Tres-illustre Prince Maurice de Nassau, Prince d'Aurenge, Gouverneur des Provinces des Païs-bas unis, General par Mer & par Terre, &c. Le tout reveu, & augmenté par Albert Girard, Samielois, Mathematicien. A Leyde. Chez Bonaventure & Abraham Elzevier, Imprimeurs ordinaires de l'Université, Anno ciƆiƆcxxxiv’.
C'est la traduction annotée de l'ouvrage de Simon Stevin, cité dans la Lettre N^o. 5, note 10.
Voici la note en question: ‘La manière parfaite est plus facile que celle que Stevin a fait, et qu'on n'a trouvé jusques à present, mais où sont ceux qui payeroient la peine de celuy qui feroit qnelque chose d'excellent? Tout va d'un si bon ordre entre les hommes, et la science si bien estimée, que c'est merveilles si on ne revient en un siècle plus barbare que celuy mesme de fer: là dessus je feray ceste question à la veuë d'un chacun;
Un romb faisant 89 degrez sur chacun meridien, iceluy commençant en un poinct de l'équateur (soit au commencement des longitudes) et progrediant du costé du septentrion d'occident vers orient, on demande combien de longitude aura un poinct dans iceluy romb, lequel a 89 degrez de latitude; et combien de circuit un tel romb a fait; finalement combien il y a de distance d'un poinct à l'autre, le tout sans tables.
On peut bien penser que celuy qui fera cela en fera bien d'autres plus faciles: la solution se fera en temps opportun, si Dieu plaist. Or selon la maniere ordinaire, qui est difficile, et tres imparfaite, la vie d'un homme n'y suffiroit pas’.

15) On rencontre ce calcul dans un petit manuscrit (le N^o. 18 du Codex Hugeniorum), qui occupe les pages vides d'un Almanac de l'année 1687, sous l'en-tête: ‘Problema Alberti Girardi in notis ad Stevini Histiodromicen. Rumbi inclinatio ad meridiem 89 gr. Item Latitudo ab aequinoctiali incipiendo aequisita 89 grad. Quaeritur quot circuitus integri, quot gradus et scrupula longitudinis conveniant itineri loxodromico’. Une page précédente de ce manuscrit contient la règle suivante, d'après laquelle le calcul a été exécuté:




‘b tangens anguli loxodromiae cum meridiano; s=HC secans arcus latitudinis acquisitae DF; t=HD tangens latitudinis acquisitae; sit r=radius DC=100000.
Aufer HD ab HC, et quaere differentiae EC logarithmum in Tabulis, quem aufer a logarithmo radii CD; reliquum multiplica per b. Productum divide per tot characteres numeri 4342944819 quot sunt characteres in logarithmis praeter characteristicam. Eritque quotiens amplitudo arcus Longitudinis in aequatore in partibus qualium radius CD continet 100000; quam amplitudinem arcus reduces ad minuta graduum faciendo ut 628318 longitudo circumferentiae, ad 360 gradus in tota circumferentia, ita amplitudo inventa ad gradus gradus in tota circumferentia, ita amplitudo inventa ad gradus longitudinis’.
Comme on le voit, cette règle revient à l'emploi de la formule correcte: λ=b.{1r-1r(secφ-tgφ)}, où φ représente la latitude du point extrême de la loxodromique et λ la différence de sa longitude avec celle du point de départ sur l'équateur.

[p. 188]

là la quadrature de l'Hyperbole; mais ce Girard avoit penetrè bien avant en plusieurs matieres de Geometrie, comme je vois par quelques endroits de ces mêmes notes. Il se trompe pourtant au commentaire sur la Statique par cordages¹⁶⁾ au sujet de la courbure de la ligne qui plie par son poids, la quelle courbure il pretend estre parabolique, et qu'il en a la demonstration.

Ma maniere pour trouver les sommes des secantes, que vous voulez scavoir, est telle. J'ajoute ensemble les secantes des arcs croissant par degrez entiers, ou par demi-degrez, jusques à l'angle donnè. De leur somme je soustrais la moitiè de l'exces dont la plus grande de ces secantes surpasse le rayon. Alors le reste aura à la somme d'autant de rayons fort pres la mesme raison (toutefois un peu plus grande) que la somme du nombre infini de secantes comprises dans l'angle donnè, à la somme d'un pareil nombre de rayons¹⁷⁾. Par exemple au rayon

16) Dans la note d'Albert Girard à laquelle Huygens fait allusion et qui se trouve à la page 508 du quatrième volume de l'ouvrage cité dans la note 14, celui-ci prétend que Stevin avait bien vu que les cordes: ‘ne sont pas en lignes droites estant estenduës, sinon que la seule corde perpendiculaire à l'horizon; car les autres cordes lasches ou fort estenduës, sont lignes paraboliques, (comme j'ay autrefois demonstré environ l'an 1617), ainsi que je demonstreray cy-après à la fin du corollaire suivant, ce qui viendra icy fort à propos pour l'ornement de cette Spartostatique’ (c'est à dire l' ‘art ponderaire par cordages’).
Toutefois, à la fin du corollaire mentionné on rencontre, au lieu de la démonstration annoncée, la note suivante: ‘Pour satisfaire à ma promesse qui precede le dernier corollaire, et n'ayant pas le loisir toutefois de mettre icy la copie de ma demonstration entière, je la donneray une autre fois au public, avec mes autres oeuvres, moyennant l'aide de Dieu, lors que la recherche des sciences sera plus recommandable, qu'elle n'est à present’.

17) Voir, pour la démonstration de cette règle et pour les résultats numériques qui vont suivre, le § I de l'Appendice N^o. 2710.

[p. 189]

10000 la somme des secantes par demi-degrez jusques à 45 degrez inclusivement est 1012061, d'où j'oste 2071, moitiè de l'exces de la secante de 45^o par dessus le rayon, reste 1009990, qui aura à la somme de 90 rayons qui fait 900000, un peu plus grande raison que le nombre infini des secantes à pareil nombre de rayons. Je trouve aussi un terme mineur¹⁸⁾ qui est 1009976, et qui est plus près du vray, mais il y a une regle de trois à faire. Suivant la Table de Snellius¹⁹⁾ la somme des secantes jusqu'à 45 degrez par minutes est 30297320, quand le rayon est 10000. Il l'a posé de 10000000, pour faire le calcul de la somme plus juste, mais apres il a retranché 3 chifres. Or je trouve par ma regle que sa Table est fautive, car non seulement la raison de la somme des secantes 30297320 à autant de rayons, qui font 27000000, mais aussi la raison de 30297320 moins 2071 à 27000000 devroit estre plus grande que celle des secantes infinies à autant de rayons. La quelle par la Regle parfaite des Logarithmes²⁰⁾ je trouve estre comme de 30299392 à 27000000. Donc la somme de Snellius est trop petite, et devroit avoir estè 30301463, scavoir 30299392 plus 2071^b). En supputant selon ma regle et par demi-degrez, je trouve 30299700 pour le terme majeur et 30299295 pour le mineur²¹⁾, ce qui confirme mon calcul, quoyque Snellius dit qu'il a fait le sien deux fois²²⁾, Il y a peut-estre quelque faute dans la Table des Secantes²³⁾. J'ay la demonstration de ma Regle mais cecy est desia trop long. De quoy au reste peut servir le calcul de ces sommes, ou leur Table, puisque par les logarithmes les Problemes se resolvent beaucoup plus parfaitement?

Ce sera quelque chose de fort beau que vostre reduction des quadratures à la quadrature du Cercle ou de l'Hyperbole, quand cela est possible, et j'espere que vous nous la communiquerez que vous l'aurez perfectionnée, ou quand mesme il

18) Voir, sur cette limite inférieure de la somme des sécantes, le § II de l'Appendice N^o. 2710.

19) La minute ajoute: qu'il appelle Canonica Logarithmorum. Cette table se trouve dans l'ouvrage cité dans la note 10, de la Lettre N^o. 2699. Elle est intitulée ‘Tabulae canonicae parallelorum’ et devait servir au calcul des loxodromes, ainsi que Snellius l'explique à la page 12 de son ouvrage.

20) C'est-à-dire au moyen de la formule exacte =1r-1r (sec φ-tgφ).

b) 4 lettres fausses tousjours [Christiaan Huygens].

21) Consultez, sur ces calculs, le § II de la pièce N^o. 2710.

22) Voir la page 13 de l'ouvrage de Snellius.

23) D'après la page citée dans la note précédente, Snellius employait pour son calcul deux tables différentes des sécantes: ‘bis eundem subduxi’, dit-il ‘semel ex tabulis secantium Thomae Finckij, iterum è tabulis Bartholomaei Pitisci; ut si quid vitij in ipsas forte tabulas operarum incurià irrepsisset, ex mutua collatione facilem haberem emendationem: cum Pitisci notae sint etiam ex opcrė Palatino expressae; illae autem Finckij aliae ab his, et ante subductae’.

[p. 190]

y manqueroit encore quelque chose. J'aimerois bien aussi de pouvoir reduire les dimensions des espaces inconnus à la mesure de quelque ligne courbe quand ces deux quadratures n'ont point de lieu, mais je le crois le plus souvent tres difficile.

Vous aviez remarquè que la soutangente de la Logarithmique est constante, mais non pas, que je scache, qu'elle representoit le quarré de l'Hyperbole.

Il me tarde de voir ce que produira Mr. Bernoulli l'ainè touchant la courbure du ressort²⁴⁾. Je n'ay pas osè esperer qu'on y aboutist à rien de clair ni d'elegant; c'est pourquoy je n'ay rien tenté.

Dans la recherche des nombres, le plus utile seroit de s'arrester aux Theoremes dont il y en a des beaux et qui peuvent servir dans des rencontres. Un certain Mr. Rolle de l'Academie des Sciences à Paris a fait imprimer quelque traitè en cette matiere²⁵⁾, que je tascheray d'avoir, car on dit qu'il est fort habile.

Vous croiez, à ce qu'il semble, qu'il ne seroit pas extrement difficile d'achever de tout point la Science des Lignes et des Nombres. En quoy je ne suis pas jusqu'icy de vostre avis, ni mesme qu'il seroit à souhaiter qu'il ne restast plus rien à chercher en matiere de Geometrie. Mais cette etude ne doit pas nous empescher de travailler à la physique, pour la quelle je crois que nous scavons assez, et plus de geometrie qu'il n'est besoin; mais il faudroit raisonner avec methode sur les experiences, et en amasser de nouvelles, à peu pres suivant le projet de Verulamius.

J'attendois depuis longtemps, selon ce que vous aviez promis, vostre methode pour les Tangentes, et je vois avec deplaisir que vous prenez à cette heure des precautions, comme doutant que je ne tiene pas ma parole. Mais quand nous envoierions en mesme temps nos escrits à Mr. Meier, comment serez vous assurè que j'auray dressè le mien de bonne foy? Si vous fuiez peut-estre le travail, j'ay encore plus de raison de l'apprehender. Car Mr. Fatio, en partant il y a deux mois pour l'Angleterre, a repris la longue lettre²⁶⁾ où il m'avoit expliquè son invention; cette lettre aiant estè si fort changée et repetassée, depuis que nous avions travaillè ensemble sur cette matiere, qu'elle estoit devenue tout autre. Ainsi je n'ay plus que les solutions des questions que nous nous proposames²⁷⁾, et il faudra que de

24) Voir, à la page 133, la Lettre N^o. 2693.

25) Démonstration d'une Methode pour résoudre les egalitez de tous les degrez; suivie de deux autres methodes, dont la première donne les moyens de résoudre ces mesmes egalitez par la Geometrie, & la seconde, pour résoudre plusieurs questions de Diophaute qui n'ont pas encore esté résolues. Par M. Rolle, de l'Académie Royale des Sciences. In-12^o. à Paris chez Jean Cusson, 1691.

26) Consultez à ce propos la Lettre N^o. 2672.

27) Voir, sur cette collaboration de Huygens et Fatio, la note 9 de la Lettre N^o. 2677.

[p. 191]

là je tire la regle. Il faut donc s'il vous plait m'exciter par vostre exemple et m'envoier sans defiance ce que vous avez promis²⁸⁾, ou laissons là nostre marchè.

Vous aurez vu ce que Mr. Bernoulli à annoncè dans le mois de Jul. de la part de son frere, qui auroit trouvè, qu'outre ma Cycloide il y a une infinitè de courbes qui servent aux reciprocations isochones²⁹⁾. Je n'y vois pas d'impossibilitè, mais je ne scaurois croire qu'il nous construise aucune de ces courbes, si ce n'est peutestre par des espaces d'etendue infinie et inconnue³⁰⁾, ce qui vaut autant que rien. Je le tiens cependant fort habile ce frere, et il me revient mieux que son ainè, qui est grandement obstinè à soutenir ce qu'il a une fois avancè. Temoin ce dernier escrit du mois de Jul., ou il nous voudroit faire accroire³¹⁾ que sa demonstration du Centre d'Oscillation (qui apres tout ne regarde que des poids enfilez en ligne droite) est plus evidente que la miene.

Je vous en fais juge et demeure de tout mon coeur etc.

28) Voir la pièce N^o. 2713.

29) Voir la fin de l'article de Jacques Bernoulli dans les Acta de Juillet 1691, notre N^o. 2690.

30) Consultez la note 10 de la présente lettre.

31) Voir la pièce N^o. 2690. Dans les notes marginales (voir la Lettre N^o. 2540, note 1) on lit, à propos de cette même démonstration, qui commence par les mots ‘Quarto, distributio’ (p. 116 du présent volume): ‘Haec omnia absurda sunt et per consequentias parum evidentes demonstrata’.