Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2690.
Jac. Bernoulli.
juillet 1691.

La pièce a été publiée dans les Acta Eruditorum¹⁾.

J.B. Demonstratio Centri Oscillationis ex Natura Vectis, reperta occasione eorum, quae super hac materia in Historia Literaria Roterodamensi recensentur, articulo 2. mens. Jun. 1690²⁾.

Ante decennium eruditus quidam Gallus Illustris³⁾ Hugenii doctrinam de Centro Oscillationis labefactaturus supposuit, celeritatem totalem penduli compositi oequari summae celeritatum partium ejus separatarum. Ego Hugenii aliquanto post suscepta causa, principii hujus falsitatem ex natura vectis demonstravi⁴⁾, juxta quam perpetuo partem celeritatis penduli in ipso axe consumi & deperdi necessum sit; quod tum sufficere poterat ad paralogismum Adversario ostendendum. Ideoque cum eadem opera determinare volebam, quanta praecise celeritatis pars in axe absumeretur, accidit mihi, ut rem quam praeter institutum esse judicabam, paulo negli-

1) De juillet 1691, pages 317 et suiv.

2) Il s'agit des pièces N^os. 2605 et 2606.

3) L'abbé de Catelan; voir la pièce N^o. 2260.

4) Voir la pièce N^o. 2426.

[p. 115]

gentius curarem, indeque in calculum inciderem ab Hugeniana Propositione abludentem, quod suspicari me fecit, diversam esse rationem vectis, cujus alterum fulcrum sit in motu, quam quae est vectis ordinarii: id quod tunc quidem aliis discutiendum reliqui, ipsemet vero materiam hanc ab eo tempore prorsus seposui. Interea praelustris & generosus quidam Vir, qui avitae Hospitaliorum gloriae nunc insuper scientiarum literarumque decus eximium addit, re maturius perpensa observavit⁵⁾, huic meo principio e vulgari vectis natura desumto apprime cum Hugeniano calculo convenire, inque eo duntaxat peccatum a me esse, quod celeritatem penduli acquisitam considerarim, cum nascentis tantum ratio habenda fuisset. Cujus correctionis certior per literas factus Hugenius approbavit methodum⁶⁾, sed difficilem eandem pronuntiat, & quaedam haud satis evidentiae continere asserit: veluti, quod celeritas vel quantitas motus penduli initialis, non acquisita spectanda sit; quod distribuendus ejus excessus eo modo quo fecimus, & quod in pendulo trium pluriumve ponderum fulcrum vectis respectu unius ponderis concipiendum sit in centro oscillationis reliquorum: miratur denique cum illustri Hospitalio, quod Propositionis suae veritatem, quam modo agnoscere videbar, calculo meo dubiam reddere coner. Ad quae sequentia notanda habeo: Primo, miror mirari Viros acutissimos, cum verba mea satis clare innuant, ex calculi istius ab Hugeniana hypothesi dissensu inferre me voluisse potius, peculiarem ut jam dixi in oscillatorio vecte obtinere communicationis motus legem, quam dictam hypothesin ullatenus suspectam reddere; quanquam, si verum fateri licet, nondum a me obtinere possum, ut hujus veritatem vel in Axiomatum numero habeam, vel ab Hugenio satis in



propatulo constitutam arbitrer, eo praesertim casu, quo pondera durante motu suo mox inter se connexa, mox soluta supponuntur⁷⁾. Secundo, ratio cur celeritas penduli initialis, non acquisita, spectanda sit, attendenti obscura esse nequit, nec mihi fuisset olim, si vel momentum speculationi inhaesissem diutius: In-

5) Voir la pièce N^o. 2605.

6) Voir la pièce N^o. 2606.

7) Allusion à la Prop. IV de la ‘Pars Quarta’ de l' ‘Horologium Oscillatorium’.

[p. 116]

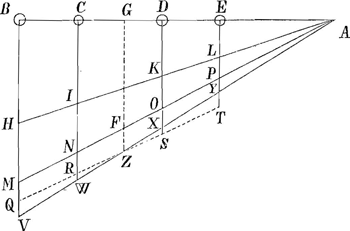
telligantur pondera quotvis B, C, D, E, virga inflexili AB connexa, junctim descendere in perpendicularibus, ut ante hac supposui: celeritates quas acquirunt eo momento quo perveniunt in H, I, K, L, sunto HM, IN, KO, LP, quae cum proportionales esse debeant ob commune vinculum ipsis ponderum distantiis ab axe AB, AC, AD, AE, sequitur, virgam cui implicata sunt ipsorum descensui cum his celeritatibus continuando nihil afferre alterationis, & propterea nullum pondus hactenus in alterum quicquam de motu suo transferre. Superest ergo solus gravitatis impulsus, qui quolibet temporis instanti acquisitis celeritatibus de novo superadditur, qui alterationem patiatur. Repraesentetur hic, (cum omnibus corporibus aequalis imprimatur) per aequales lineolas MQ, NR, OS, PT, quae quidem respectu celeritatum acquisitarum HM, IN, KO, LP, uti hae ipsae respectu spatiorum percursorum BH, CI, DK, EL, habendae pro incomparabiliter parvis, sic ut haec tria QM, MH, HB, habeant se quodammodo, ut linea, superficies & corpus. At vero ob interpositam virgam fieri nequit, ut pondera simul sint in punctis Q, R, S & T, hoc est, in recta QT parallela ipsi MA; quin potius in directum jacere debent cum axe A, secundum rectam VWXY, adeo ut cum pondera axi propiora terminos suos S & T nondum attigerunt, remotiora suos Q & R jam praeterierint, parte residua virium gravitatis ab illis in haec translata, parte in axe absumta. Tertio, in pendulo trium pluriumve ponderum centrum oscillationis omnium excepto uno considerat Hospitalius ceu fulcrum respectu reliqui. Hoc quia inevidens judicat Hugenius (quanquam verum deprehendam) & praeterea quia ad demonstrationem aliter quam per inductionem instituendam parum aptum, malo rem invertere, & pondus duntaxat extimum habere loco fulcri, quod ferat reliqua pondera omnia suis quaeque locis vectem urgentia. Quarto, distributio seu translatio quantitatis motus (olim solas celeritates consideravi, quia pondera supposui aequalia) nihil obscuritatis habere tandem potest, fluitque ex natura vectis ordinarii: nimirum ponderis D incrementum celeritatis extra virgam est OS, in virga tantum OX, residuum XS, quantitas ergo motus transferenda tum in axem tum in pondus extimum D×XS⁸⁾; unde AB est ad AD, sicut D×XS ad D×AD×XS/AB portionem quantitatis motus transferendam in solum pondus B: Similiter portio, quam de motu suo pondus E in pondus B transmittit, est E×AE×YT/AB. At pondus C, quod majus celeritatis incrementum in virga quam extra virgam accipit, motui ponderis B contraria ratione adimere censendum est portionem C×AC×WR/AB. Est vero totum incrementum quantitatis motus, quod ponderi extimo B a reliquis ponderibus

8) L'imprimé des ‘Acta’ a remplacé, ici et dans les formules qui suivent, le signe × par x.

[p. 117]

accedit, praeter id quod a propria gravitate nanciscitur, B×VQ: tandem sit Z intersectio rectarum QT, VY, & ducatur GZ parallela rectis BV, CW, &c.

Quibus positis centrum oscillationis sic invenitur: Per hypothesin & ex natura vectis est, E×AE×YT+D×AD×XS-C×AC×WR/AB=B×VQ, quare aeque multiplicando & addendo erit, E×AE×YT+D×AD×XS=C×AC×WR+B×AB×VQ seu (quia YT, XS, WR, VQ, ipsis ZY, ZX, ZW, ZV, vel ipsis GE, GD, GC, GB, proportionalia) E×AEG⁹⁾+D×ADG=C×ACG+B×ABG, additisque utrique parti tum E×AEq+D×ADq, tum C×CAG+B×BAG, fiet E×EAG+D×DAG+C×CAG+B×BAG=E×AEq+D×ADq+C×ACq+B×ABq; unde tandem AG=B×ABq+C×ACq+D×ADq+E×AEq/B×AB+C×AC+D×AD+E×AE. Si quaedam pondera ultra axem ex adversa parte constituta sint, eadem pro AG invenitur quantitas, nisi quod membra denominatoris ponderibus istis respondentia fiant negativa.

Jam vero puncti G a virga ponderibus B, C, D & E gravata abrepti & per rectam GZ descendentis, incrementum celeritatis, cum pervenit ad F, necessario est FZ, quae est aequalis, ob Parallelogrammum FQ, ipsi MQ vel NR &c. incremento scil. velocitatis, quod pondus quodlibet separatim descendens a propria gravitate acquirit; quod cum similiter valeat in omnibus spatii GZ partibus, sequitur, spatium istud, hoc est, angulum GAZ eodem tempore pertransiri a virga, sive omnibus ponderibus B, C, D & E, sive unico tantum pondere in G gravata, & proin G fore centrum oscillationis, quod itaque repertum est. Neque variat demonstratio pro pendulo ordinario, cui pondera ita inhaerent, ut per arcus circulorum descendere cogantur: cumque reperta quantitas AG eadem sit cum illa, quae alias pro centro percussionis invenitur, sequitur, centrum oscillationis & percussionis corporum, ut recte notavit Hugenius, unum idemque esse, quanquam Wallisius¹⁰⁾ in Cono ex. gr. aliud percussionis, Hugenius aliud oscillationis centrum assignat: fallitur enim Wallisius in eo, quod integrae basi Coni circulisque basi parallelis non majorem distantiam ab axe rotationis celeritatemque tribuit ea, quam ipsa horum circulorum centra obtinent. Haec vero centri oscillationis demonstratio sic reformata, uti generalis est & facilis, inque Geometrica exactitudine Hugenianoe neutiquam cedit, sic eidem in eo praeferenda videtur, quod principium vectis, quo nititur, indubitatum est ac evidens, cum Hugeniana hypothesis obscura fere fit, nec aliam ob causam pro vera habeatur, quam quod nihil in contrarium afferri possit, intellige in solidis corporibus: in liquidis enim res magis dubia videtur; cum vix appareat, quomodo cum ista hypothesi conciliari possit spontaneus communis centri gravitatis ascensus, qui

9) C'est-à-dire: E×AE×EG+D×AD×DG, etc.

10) Voir, sur ce que va suivre, les notes 2 et 3 de la pièce N^o. 2606.

[p. 118]

accidit, cum metallum in imo liquoris acidi positum ac dissolutum, aut liquor levior graviori leniter superinfusus eidem sensim permiscetur; id quod ansa & fundamentum extitit Perpetui Mobilis nuper a Fratre¹¹⁾ inventi¹²⁾ ac in Actis publicati¹³⁾, cui proin ibidem subjunctam stricturam neutiquam officere existimamus. Caeterum collegeram, quod si celeritas totalis penduli compositi minor esse debeat summa celeritatum partium ejus separatarum, reliquum in axe premendo consumi necessum sit. Negat Hugenius hanc consequentiam, dicendo, saepenumero deperdi aliquid de motu, quod nullibi insumatur: at ego contra sentio, si quid amittatur, illud perpetuo alicubi impendi, sed quandoque in premendo firmo obice, quandoque in tollendo motu contrario, adeo ut cum penduli nostri pondera moveantur in eandem partem, jure inferre potuerim, motum deperditum necessario in axe premendo consumtum esse. Denique & illud dubium est, quod mihi objicit Vir acutissimus, effectum videlicet resistentiae aeris, disruptionis vinculi, quod partes penduli connectit, aliorumque obstaculorum indeterminatae quantitatis esse, minuique in infinitum posse, sic ut non tollat (ut existimaram) possibilitatem motus perpetui, qui alias obtineret, si sine his impedimentis centrum gravitatis penduli altius ascendere quam descendere supponeretur. Constat enim, id quod de motu communicatur aut absumitur occursu obstaculorum, ad celeritatem mobilis, & hanc ad motus altitudinem determinatam semper relationem obtinere. Tantum de his. Notum occasione praesentis materiae Eruditis facio, Fratrem meum observasse

11) Johannes Bernoulli, né à Bâle le 27 juillet 1667, mort dans cette même ville le 1^er janvier 1748. De même que son frère Jacob (voir la Lettre N^o. 2332, note 1) il eut a vaincre l'opposition de son père pour s'appliquer aux sciences mathématiques. En 1691 il visita Paris, où commencèrent ses relations avec de l'Hospital, sur lesquelles on peut consuiter les pages 222-226 du Tome III des ‘Vorlesungen über Geschichte der Mathematik’ de M. Cantor (édition de 1901). En 1695 il fut nommé professeur à l'Université de Groningen; dix ans plus tard il succéda à son frère, Jacob, dans la chaire de Bâle, qu'il occupa jusqu'à la fin de sa vie. Deux de ses fils, Nicolas, né à Bâle le 27 janvier 1695, mort à St. Petersbourg le 6 août 1726, et Daniel, né à Groningen le 8 février 1700, mort à Bâle le 17 mars 1782, se sont distingués comme mathématiciens, surtout le dernier, bien connu par ses recherches d'hydrodynamique et sa théorie de l'élasticité des gaz.

12) Ce mobile perpetuum se trouve décrit dans son essai:
Dissertatio Chymico-Physica de Effervescentia & Fermentatione, nova hypothesi fundata, cum descriptione alicujus perpetui mobilis pure artificialis, autore Johanne Bernoulli Basiliensi. Basileae. Typis Jac. Bertschii 1690. in-4^o.
Bernoulli imagine un mélange de deux liqueurs d'inégale densité dans un vase. Un tube de verre y est plongé verticalement de manière que le bout supérieur ouvert dépasse le niveau du liquide. Le bout inférieur est fermé par une membrane que Bernoulli suppose perméable seulement pour la moins dense des deux liqueurs. Celle-ci monterait dans le tube et s'écoulerait continuellement par l'orifice supérieur.

13) Voir les ‘Acta Eruditorum’ de février 1691.

[p. 119]

quod praeter Hugenii Cycloidem infinitae dentur curvae, per quas descendens grave oscillationes peragat isochronas¹⁴⁾: item non solum cum Newtono & Tschirnhausio¹⁵⁾ infinitas cycloides animadvertisse, quae sui evolutione seipsas describant, sed & detexisse quampiam ex alio quam cycloidalium genere¹⁶⁾, quae eadem proprietate gaudeat.

14) Il n'en est rien; aussi Jean Bernoulli n'y est jamais revenu.

15) Consultez les notes 18 et 19 de la pièce N^o. 2626.

16) Il s'agit de la spirale logarithmique, comme il résulte du § 9 d'un article publié par Jacques Bernoulli dans les ‘Acta Eruditorum’ de mai 1692, sous le titre: ‘Lineae Cycloidales, Evolutae, Ant-Evolutae, Causticae, Anti-Causticae, Peri-Causticae. Earum usus & simplex relatio ad se invicem. Spira mirabilis. Aliaque per I.B.’